このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
数値軌道伝播を用いた衛星シナリオにおける月自由帰還軌跡のモデル化
この例では、satelliteScenario を使用して月の自由帰還軌跡をシミュレートします。検討中の月自由帰還軌道は、まず宇宙機を地球から月まで運ぶ月周回軌道です。その後、宇宙機は月の裏側で重力アシストを実行し、地球に戻ります。自由帰還軌跡では、最初の月周回軌道投入燃焼後の中間操作は行われません。月周回軌道投入燃焼は、宇宙機を自由帰還軌道に乗せるために地球の駐機軌道上で実行される操作です。このような軌道の利点は、推進システムが故障しても宇宙機が地球に戻ってくることが保証されることです。これは、人類の月面探査ミッションにとって、地球近傍空間で立ち往生する可能性や、地球・月系から脱出して太陽中心軌道に入る可能性を回避するために極めて重要です。
この例では、地球の重力ポテンシャルモデルが質点に設定されています。サポートされているすべての太陽系天体の第三の天体の重力が考慮されます。シナリオは月周回軌道投入燃焼直後に始まります。シナリオは、宇宙機が地球に戻り、高度 60 km の近点に到達すると終了します。
衛星シナリオの作成
satelliteScenario オブジェクトを作成する。StartTime を 2022 年 11 月 17 日PM2 時 40 分 (UTC) に、StopTime を 2022 年 11 月 24 日PM12 時 45 分 (UTC) に、SampleTime を 60 秒に設定します。
startTime = datetime(2022,11,17,14,40,0);
stopTime = datetime(2022,11,24,12,45,0);
sampleTime = 60; % s
sc = satelliteScenario(startTime,stopTime,sampleTime)sc =
satelliteScenario with properties:
StartTime: 17-Nov-2022 14:40:00
StopTime: 24-Nov-2022 12:45:00
SampleTime: 60
AutoSimulate: 1
Satellites: [1×0 matlabshared.satellitescenario.Satellite]
GroundStations: [1×0 matlabshared.satellitescenario.GroundStation]
Platforms: [1×0 matlabshared.satellitescenario.Platform]
Viewers: [0×0 matlabshared.satellitescenario.Viewer]
AutoShow: 1
数値プロパゲーターを追加
シナリオに数値軌道プロパゲーターを追加します。常微分方程式 (ODE) ソルバー オプション、重力ポテンシャル モデル、第三の天体の重力を構成します。サポートされているすべての太陽系の天体から第三の天体の重力を含めます。数値伝播関数は、地球の大気からの抗力と太陽放射圧による摂動の組み込みもサポートしていることに注意してください。ただし、この例ではこれらの効果は無視されます。
numericalPropagator(sc, ... ODESet=odeset(RelTol=1e-8,AbsTol=1e-8,MaxStep=300), ... IncludeThirdBodyGravity=true, ... ThirdBodyGravitySource=["Sun" "Mercury" "Venus" "Moon" "Mars" "Jupiter" "Saturn" "Uranus" "Neptune" "Pluto"], ... GravitationalPotentialModel="point-mass")
ans =
NumericalPropagatorOptions with properties:
ODESolver: "ode45"
ODESet: [1×1 struct]
GravitationalPotentialModel: "point-mass"
IncludeAtmosDrag: 0
IncludeThirdBodyGravity: 1
ThirdBodyGravitySource: ["Sun" "Mercury" "Venus" "Moon" "Mars" "Jupiter" "Saturn" "Uranus" "Neptune" "Pluto"]
IncludeSRP: 0
PlanetaryEphemerisModel: "de405"
初期接触要素を計算する
ICRF で宇宙機の初期位置と速度を定義します。これらは、月周回軌道投入燃焼直後の宇宙機の状態を表しています。これらの状態の計算はこの例の範囲外ですが、非線形制約最適化手法を使用して計算し、初期速度の大きさを最小限に抑えることができます。
initialPosition = ... [5927630.386747557; ... 3087663.891097251; ... 1174446.969646237]; % m initialVelocity = ... [-5190.330300215130; ... 8212.486957313564; ... 4605.538019512981]; % m/s
ICRF の位置と速度を接触要素に変換します。接触要素は、摂動を無視した場合に宇宙機がたどる軌道に対応する瞬間的なケプラー要素です。
[semiMajorAxis, ... eccentricity, ... inclination, ... rightAscensionOfAscendingNode, ... argumentOfPeriapsis, ... trueAnomaly] = ijk2keplerian(initialPosition,initialVelocity)
semiMajorAxis =
2.118144315642977e+08
eccentricity = 0.967962522906465
inclination = 27.516388036479892
rightAscensionOfAscendingNode = 7.800979911647819
argumentOfPeriapsis = 21.999999999999996
trueAnomaly =
0
シナリオに宇宙機を追加する
satellite 関数を使用して、計算された接触要素を使用してシナリオに宇宙機を追加します。数値プロパゲーターを宇宙機に割り当てます。
craft = satellite(sc, ... semiMajorAxis, ... eccentricity, ... inclination, ... rightAscensionOfAscendingNode, ... argumentOfPeriapsis, ... trueAnomaly, ... OrbitPropagator="numerical", ... Name="Spacecraft")
craft =
Satellite with properties:
Name: Spacecraft
ID: 1
PhysicalProperties: [1x1 Aero.satellitescenario.satellite.PhysicalProperties]
ConicalSensors: [1x0 matlabshared.satellitescenario.ConicalSensor]
Gimbals: [1x0 matlabshared.satellitescenario.Gimbal]
Transmitters: [1x0 satcom.satellitescenario.Transmitter]
Receivers: [1x0 satcom.satellitescenario.Receiver]
Accesses: [1x0 matlabshared.satellitescenario.Access]
Eclipse: [1x0 Aero.satellitescenario.Eclipse]
GroundTrack: [1x1 matlabshared.satellitescenario.GroundTrack]
Orbit: [1x1 matlabshared.satellitescenario.Orbit]
CoordinateAxes: [1x1 matlabshared.satellitescenario.CoordinateAxes]
OrbitPropagator: numerical
MarkerColor: [0.059 1 1]
MarkerSize: 6
ShowLabel: true
LabelFontColor: [1 1 1]
LabelFontSize: 15
Visual3DModel:
Visual3DModelScale: 1
プロパティ PhysicalProperties は、大気抵抗と太陽放射圧の計算で使用される宇宙機の物理的特性を定義します。これらの特性は現在デフォルト値を使用しており、この例では大気抵抗と太陽放射圧が無視されているため使用されていません。
craft.physicalProperties
ans =
PhysicalProperties with properties:
Mass: 4
DragCoefficient: 2.179000000000000
DragArea: 1
ReflectivityCoefficient: 1.800000000000000
SRPArea: 1
シナリオに月を追加
シナリオを視覚化するために使用される衛星シナリオ ビューアーは、すでに月の視覚化をレンダリングしています。ただし、月の軌道もプロットすると、状況認識が向上します。これを行うには、satellite 関数を使用して、月と同じ軌跡にある衛星をシナリオに追加します。月の軌跡を計算するには、まずシナリオ時間サンプルの重心力学時間 (TDB) をユリウス通日として計算します。
utc = startTime:seconds(60):stopTime; leapSeconds = 37; % s ttMinusTAI = 32.184; % s terrestrialTime = utc + seconds(leapSeconds + ttMinusTAI); tdbJD = tdbjuliandate([ ... terrestrialTime.Year' ... terrestrialTime.Month' ... terrestrialTime.Day' ... terrestrialTime.Hour' ... terrestrialTime.Minute' ... terrestrialTime.Second']);
planetEphemeris を使用して各シナリオ時間サンプルの月の位置を計算し、その位置を時刻表に変換します。
pMoonkm = planetEphemeris(tdbJD,"earth","moon"); % km pMoon = convlength(pMoonkm,'km','m'); % m pMoonTT = timetable(utc',pMoon);
satellite 関数を使用して、月を表す衛星をシナリオに追加します。軌道とマーカーの色を赤に設定します。
moon = satellite(sc,pMoonTT,Name="Moon"); moon.Orbit.LineColor="red"; moon.MarkerColor="red";
地球にラベル付けする
このシナリオに関係する距離のスケールは非常に大きいため、影の側から見ると地球が容易に見えない可能性があります。これを軽減するには、地球の北極に地上局を追加し、「地球」というラベルを付けます。この地上局のマーカー サイズを 0.001 に設定します。こうすることで、「地球」というラベルが地球の位置の近くに表示されます。
earth = groundStation(sc, ... 90, ... % Latitude, deg 0, ... % Longitude, deg Name="Earth"); earth.MarkerSize = 0.001;
シナリオを可視化する
satelliteScenarioViewer を実行して衛星シナリオ ビューアーを起動します。再生速度の乗数を 60,000 に設定します。カメラの基準座標系を「慣性」に設定します。
v = satelliteScenarioViewer(sc, ... CameraReferenceFrame="Inertial", ... PlaybackSpeedMultiplier=60000);
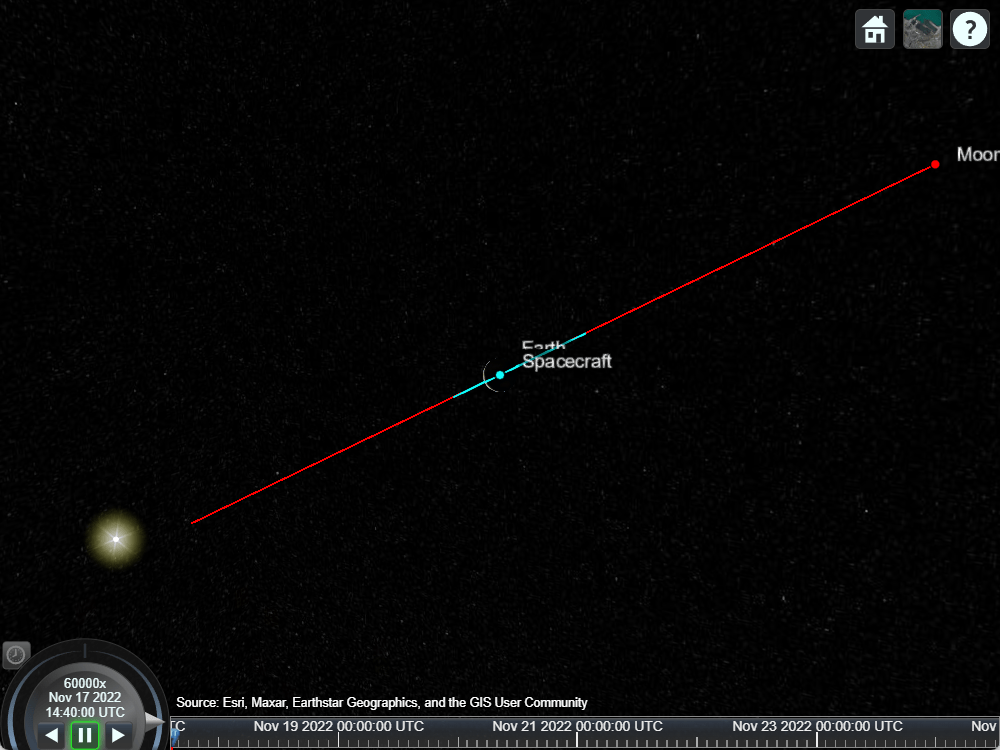
カメラの位置と向きを設定して、フリーリターン軌道を上から見た図で可視化します。
campos(v, ... 55.991361, ... % Latitude, deg 18.826434, ... % Longitude, deg 1163851259.541816); % Altitude, m camheading(v, ... 359.7544952991605); % deg campitch(v, ... -89.830968253450209); % deg camroll(v, ... 0); % deg
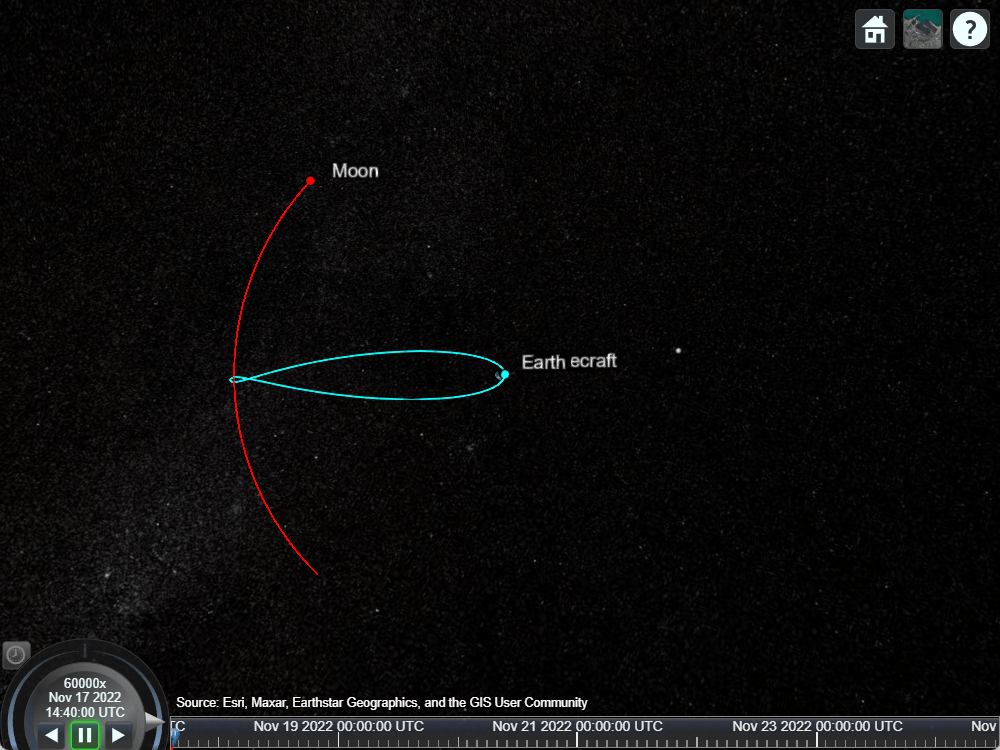
シナリオを再生します。
play(sc);
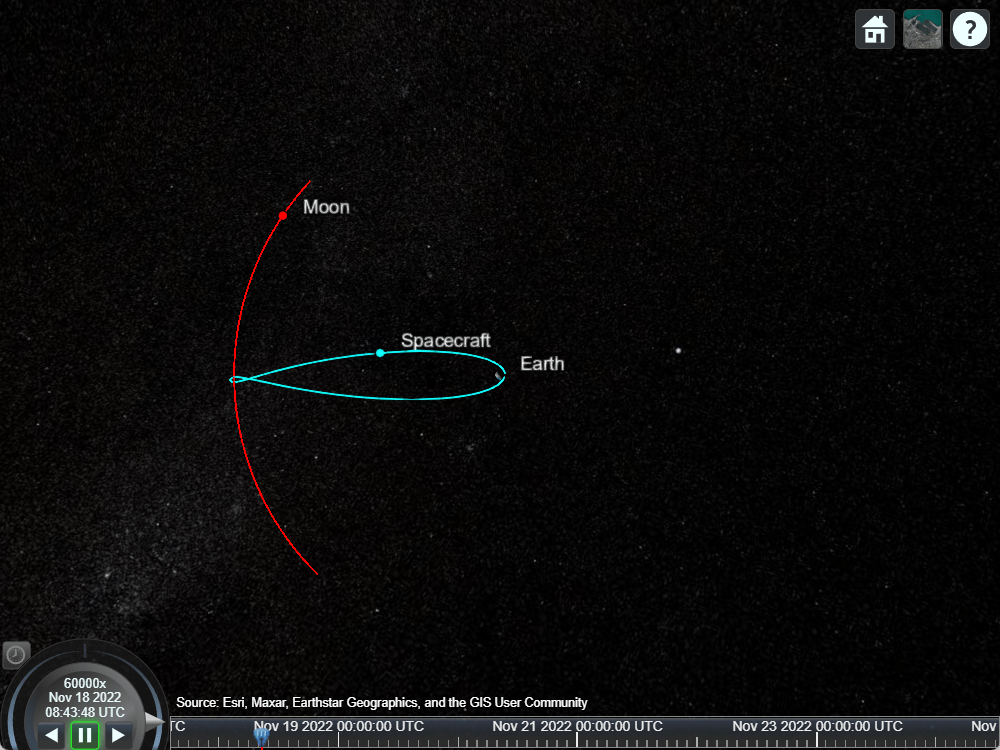
月面遭遇をよりよく見えるように、カメラの位置を手動で変更します。左クリックしてドラッグすると回転し、右クリックしてドラッグすると前後に移動します。あるいは、スクロール ホイールを使用して前後に翻訳することもできます。
