このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

軌道伝播法

Aerospace Toolbox は、2 つのトップレベルの軌道伝播方法をサポートしています。Kepler (unperturbed) と Numerical (high precision) 。

ケプラー（不動）

ケプラー軌道伝播は、ケプラーの惑星運動の法則に基づいて、宇宙空間における物体の位置と速度を数値的に計算し、予測するプロセスです。ケプラーの法則は、太陽の周りを回る惑星など、中心天体の周りを楕円軌道で回る物体の運動を数学的に記述します。

ケプラーの軌道を伝播するには、通常、次の要素が必要です。

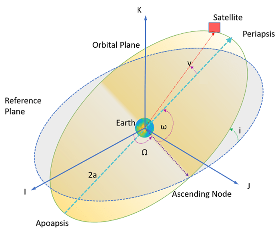
この図では、軌道面 (黄色) が 基準面 (灰色) と交差しています。地球周回衛星の場合、基準面は通常、GCRF の IJ 平面です。

次の 2 つの要素は楕円の形状とサイズを定義します。

• 離心率 (e) — 円と比較した場合、楕円の形状がどの程度細長いかを説明します。

• 長半径 (a) — 近点距離と 遠点距離の合計を 2 で割った値。近点とは、軌道を回る物体が、その物体の質量の中心に最も近づく点のことです。遠点とは、軌道を回る物体が、その物体の質量の中心から最も遠い点のことです。典型的な二体軌道の場合、長半径は天体の中心間の距離です。

これら 2 つの要素は、楕円が埋め込まれる軌道面の方向を定義します。

• 傾斜 (i) — 昇交点で測定された基準面に対する楕円の垂直傾斜。昇交点とは、軌道が基準面を上向きに通過する場所です (図の緑色の角度 i)。傾斜角は、軌道面と基準面の交線に対して垂直に測定されます。楕円上の任意の 3 つの点によって、楕円軌道面が定義されます。

  赤道軌道から始めて、軌道面を上方に傾けることができます。赤道から上方に傾いている角度は、傾斜角、i と呼ばれ、[0,180] の範囲にあります。地球の中心は常に軌道面内にあるため、衛星が軌道を北上する途中で赤道を通過する軌道上の点は昇交点となり、衛星が南下する途中で赤道を通過する軌道上の点は 降交点 となります。赤道上のこれらの 2 つの点を通る線を描くと、ノードのラインが定義されます。

• 昇交点赤経 (Ω) — 参照フレームの I 軸に対する、楕円の昇交点 (軌道が参照面を上向きに通過する場所) の水平方向。昇交点赤経 (RAAN) の回転は、0° から 360° までの任意の数値になります。

残りの 2 つの要素は次のとおりです。

• 近点引数 (ω) — 軌道面における楕円の向き。昇交点から近点までの範囲で測定された角度。範囲は [0, 360)。

• 真近点 (v) — 特定の時刻における楕円軌道上の天体の位置。衛星の軌道上の位置は近点から反時計回りに測定され、[0, 360) の範囲の 真近点角、ν と呼ばれます。

これらのパラメータを使用して、数値積分やケプラーの方程式などの数値手法を使用して軌道を伝播できます。これらのメソッドを使用すると、特定の時間におけるオブジェクトの位置と速度を計算できます。これらの各要素の詳細については、軌道要素 を参照してください。

Aerospace Toolbox は、ユニバーサル変数とニュートン・ラプソン反復法を使用して、衛星の軌道を時間の経過とともに伝播します。この分析アルゴリズムは高速ですが、制限があります。伝播軌道は中心天体の球状（質点）重力のみを考慮します。この定式化には他の摂動は含まれません。

この伝播方法は、常に中心天体の中心を原点とする ICRF 慣性座標系で実行されます。初期慣性位置 r₀ と時刻 t₀ での速度 v₀ が与えられている場合、まず軌道エネルギー ξ と軌道長半径の逆数 α を求めます。

$\begin{array}{l}\xi =\frac{v_0{}^2}{2}-\frac{\mu }{r_0}\\ \alpha =\frac{-2\xi }{\mu },\end{array}$

ここで、μ は中心天体の標準重力パラメータです。次に、α の符号から軌道の種類を決定します。

• α>0 => 円形または楕円形

• α<0 => 双曲

• α ≈0 => 放物線

ニュートン・ラプソン反復法を初期化するには、軌道タイプに基づいて χ の初期推定値を選択します。

• 円形または楕円形の軌道

  ${\chi }_0\approx \sqrt{\mu }(\Delta t)\alpha ,$

  ここで、Δ t は伝播ステップサイズ（シミュレーション時間ステップ）です。Δ t が軌道周期 $T=2\pi \sqrt{\frac{a^3}{\mu }}$ を超える場合は、 Δ t をラップします。

• 放物線軌道

  ${\chi }_0\approx \sqrt{p}2\cot (2w),$

  ここで、

  $\begin{array}{l}\overrightarrow{h}=\overrightarrow{r_0}\times \overrightarrow{v_0}\\ p=\frac{h\cdot h}{\mu }\\ \cot (2s)=3\sqrt{\frac{\mu }{p^3}}(\Delta t)\\ {\tan }^3(w)=\tan (s).\end{array}$

• 双曲軌道:

  ${\chi }_0\approx \text{sign}(\Delta t)\sqrt{-\frac{1}{\alpha }}\ln (\frac{-2\mu \alpha (\Delta t)}{\overrightarrow{r_0}\cdot \overrightarrow{v_0}+\text{sign}(\Delta t)\sqrt{-\frac{\mu }{\alpha }}(1-r_0\alpha )}).$

  |x_n-x_n-1| > tolerance の間、ニュートン・ラプソン反復法を実行します。

  $$\begin{array}{l}{\chi }_{n+\text{1}}={\chi }_n+\frac{\sqrt{\mu }(\Delta t)-{\chi }_n{}^3{c}_3-\frac{\overrightarrow{r_0}\cdot \overrightarrow{v_0}}{\sqrt{\mu }}{\chi }_n{}^2{c}_2-r_0{\chi }_n(1-\psi c_3)}{{\chi }_n{}^2{c}_2+\frac{\overrightarrow{r_0}\cdot \overrightarrow{v_0}}{\sqrt{\mu }}{\chi }_n(1-\psi c_3)+r_0(1-\psi c_2)}\\ {\chi }_n\Leftarrow {\chi }_{n+\text{1}},\end{array}$$

  ここで、

  $$\psi ={\chi }_n{}^2\alpha .$$

  (ψ>0の場合)

  $\begin{array}{l}{c}_2=\frac{1-\cos (\sqrt{\psi })}{\psi }\\ c_3=\frac{\sqrt{\psi }-\sin (\sqrt{\psi })}{\sqrt{{\psi }^3}}.\end{array}$

  (ψ<0の場合)

  $\begin{array}{l}{c}_2=\frac{1-\cosh (\sqrt{-\psi })}{\psi }\\ c_3=\frac{\sinh (\sqrt{-\psi })-\sqrt{-\psi }}{\sqrt{{(-\psi )}^3}}.\end{array}$

  （ψ ≈0の場合）、

  $\begin{array}{l}{c}_2=\frac{1}{2}\\ c_3=\frac{1}{6}.\end{array}$

  ユニバーサル変数 $$f$$、$$\dot{f}$$、$$\text{g}$$、$$\dot{g}$$ を計算します。

  $\begin{array}{l}f=1-\frac{{\chi }_n{}^2}{r_0}{c}_2\\ \dot{f}=\frac{\sqrt{\mu }}{r{r}_0}{\chi }_n(\psi c_3-1)\\ g=(\Delta t)-\frac{{\chi }_n{}^3}{\sqrt{\mu }}{c}_3\\ \dot{g}=1-\frac{{\chi }_n{}^2}{r}{c}_2.\end{array}$

  位置と速度の出力ベクトルを組み立てます。

  $\begin{array}{l}\overrightarrow{r_{\text{icrf}}}=f\overrightarrow{r_0}+g\overrightarrow{v_0}\\ \overrightarrow{v_{\text{icrf}}}=\dot{f}\overrightarrow{r_0}+\dot{g}\overrightarrow{v_0}.\end{array}$

数値（高精度）

このオプションは、Simulink^® ソルバーを使用して、各シミュレーション タイムステップ (Δ t) での中心体の重力加速度からの位置と速度を積分します。中心物体の加速度を計算する方法は、Gravitational potential model パラメータの現在の設定によって異なります。A_icrf (適用された加速度) 入力ポートを使用して、伝播アルゴリズムにカスタム加速度コンポーネントを含めることもできます。非球面加速度項を含む重力モデルの場合、ブロックは固定フレーム座標系 (地球の場合は ITRF) で非球面重力を計算します。ただし、数値積分は常に慣性 ICRF 座標系で実行されます。したがって、各タイムステップで次のようになります。

1. ブロックは位置と速度の状態を固定フレームに変換します。

2. ブロックは固定フレーム内の非球面重力を計算します。

3. ブロックは結果として生じる加速度を慣性フレームに変換し、そこで他の加速度項と合計して積分します。

$$\begin{array}{l}\overrightarrow{a_{\text{icrf}}}={\overrightarrow{a}}_{\text{central}\text{body}\text{gravity}}+{\overrightarrow{a}}_{\text{drag}}+{\overrightarrow{a}}_{\text{thirdbody}}+{\overrightarrow{a}}_{\text{srp}}+{\overrightarrow{a}}_{\text{applied}}\\ \overrightarrow{a_{\text{icrf}}}\underset{\text{integrate}}{\Rightarrow }\overrightarrow{r_{\text{icrf}}},\overrightarrow{v_{\text{icrf}}}\end{array}$$

中心物体

中心物体の加速度を計算する方法には、質点法、扁平楕円体法、球面調和関数法などがあります。

• 質点 — このオプションは、ニュートンの万有引力の法則を使用して球状重力の影響のみを含め、中心物体を質点として扱います。

  ${\overrightarrow{a}}_{\text{centralbodygravity}}=-\frac{\mu }{r^2}\frac{\overrightarrow{r_{\text{icrf}}}}{r},$

  ここで、μ は中心天体の標準重力パラメータです。

• 扁平楕円体 (J2) — このオプションでは、球状の重力に加えて、中心天体の扁平度を考慮した 2 次帯状調和重力係数 J₂ の摂動効果が組み込まれています。J₂ は、中心天体の完全な球体からの重力偏差の大部分を占めます。

  $${\stackrel{\rightharpoonup }{a}}_{centralbodygravity}=-\frac{\mu }{r^2}\frac{\overrightarrow{r_{\text{icrf}}}}{r}+fixed2inertial({\stackrel{\rightharpoonup }{a}}_{nonspherical}),$$

  ここで、

  $$\begin{array}{l}{\overrightarrow{a}}_{\text{nonspherical}}=\\ \{[\frac{1}{r}\frac{\partial }{\partial r}U-\frac{r_{\text{ff}}{}_{{}_k}}{r^2\sqrt{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}}\frac{\partial }{\partial \varphi }U]r_{\text{ff}}{}_{{}_i}\}i\\ +\{[\frac{1}{r}\frac{\partial }{\partial r}U+\frac{r_{\text{ff}}{}_{{}_k}}{r^2\sqrt{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}}\frac{\partial }{\partial \varphi }U]r_{\text{ff}}{}_{{}_j}\}j\\ +\{\frac{1}{r}(\frac{\partial }{\partial r}U)r_k+\frac{\sqrt{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}}{r^2}\frac{\partial }{\partial \varphi }U\}k,\end{array}$$

  球座標における偏微分が与えられると：

  $\begin{array}{l}\frac{\partial }{\partial r}U=\frac{3\mu }{r^2}{(}^{\frac{R_{\text{cb}}}{r}}{P}_{2,0}[\sin (\varphi )]J_2\\ \frac{\partial }{\partial \varphi }U=-\frac{\mu }{r}{(}^{\frac{R_{\text{cb}}}{r}}{P}_{2,1}[\sin (\varphi )]J_2\end{array}$

  ここで、

  • ϕ および λ — 衛星の地心緯度と経度。

  • P_2,0 と P_2,1 — ルジャンドル関数。

  • μ — 中心天体の標準重力パラメータ。

  • R_cb — 中心天体の赤道半径。

  変換 fixed2inertial は、遠心加速度とコリオリ加速度を考慮して、固定フレームの位置、速度、加速度を中心物体の中心を原点とする ICRF 座標系に変換します。各中心天体に使用される固定座標系と慣性座標系の詳細については、 を参照してください。

• 球面調和関数 — このオプションは、ゾーン、セクター、テッセラル調和関数を考慮した高次の摂動効果を含めることで忠実度を高めます。参考までに、2 次、0 次ゾーン調和関数 J₂=-C₂₀ です。球面調和関数モデルは、中心天体とジオポテンシャル モデルによって異なる最大次数 l=l_max までの調和関数を考慮します。

  $${\stackrel{\rightharpoonup }{a}}_{centralbodygravity}=-\frac{\mu }{r^2}\frac{\overrightarrow{r_{\text{icrf}}}}{r}+fixed2inertial({\stackrel{\rightharpoonup }{a}}_{nonspherical}),$$

  ここで、

  $$\begin{array}{l}{\stackrel{\rightharpoonup }{a}}_{nonspherical}=\\ \left\{\left[\frac{1}{r}\frac{\partial }{\partial r}U-\frac{r_{\text{ff}}{}_{{}_k}}{r^2\sqrt{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}}\frac{\partial }{\partial \varphi }U]r_{\text{ff}}{}_{{}_i}-[\frac{1}{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}\frac{\partial }{\partial \lambda }U\right]r_{\text{ff}}{}_{{}_j}\right\}i\\ +\left\{\left[\frac{1}{r}\frac{\partial }{\partial r}U+\frac{r_{\text{ff}}{}_{{}_k}}{r^2\sqrt{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}}\frac{\partial }{\partial \varphi }U]r_{\text{ff}}{}_{{}_j}+[\frac{1}{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}\frac{\partial }{\partial \lambda }U\right]r_{\text{ff}}{}_{{}_i}\right\}j\\ +\left\{\frac{1}{r}(\frac{\partial }{\partial r}U)r_{\text{ff}}{}_{{}_k}+\frac{\sqrt{r_{\text{ff}}{{}_{{}_i}}^2+r_{\text{ff}}{{}_{{}_j}}^2}}{r^2}\frac{\partial }{\partial \varphi }U\right\}k,\end{array}$$

  球座標における次の偏微分が与えられます。

  $$\begin{array}{l}\frac{\partial }{\partial r}U=-\frac{\mu }{r^2}\underset{l=2}{\overset{l_{\max }}{{{\displaystyle \sum }}^{\text{}}}}\underset{m=0}{\overset{l}{{{\displaystyle \sum }}^{\text{}}}}{(}^{\frac{R_{\text{cb}}}{r}}(l+1)P_{l,m}[\sin (\varphi )]\{C_{l,m}\cos (m\lambda )+S_{l,m}\sin (m\lambda )\}\\ \frac{\partial }{\partial \varphi }U=\frac{\mu }{r}\underset{l=2}{\overset{l_{\max }}{{{\displaystyle \sum }}^{\text{}}}}\underset{m=0}{\overset{l}{{{\displaystyle \sum }}^{\text{}}}}{(}^{\frac{R_{\text{cb}}}{r}}\{P_{l,m+1}[\sin (\varphi )]-(m)\tan (\varphi )P_{l,m}[\sin (\varphi )]\}\{C_{l,m}\cos (m\lambda )+S_{l,m}\sin (m\lambda )\}\\ \frac{\partial }{\partial \lambda }U=\frac{\mu }{r}\underset{l=2}{\overset{l_{\max }}{{{\displaystyle \sum }}^{\text{}}}}\underset{m=0}{\overset{l}{{{\displaystyle \sum }}^{\text{}}}}{(}^{\frac{R_{\text{cb}}}{r}}(m)P_{l,m}[\sin (\varphi )]\{S_{l,m}\cos (m\lambda )-C_{l,m}\sin (m\lambda )\},\end{array}$$

  ここで、

  • ϕ および λ — 衛星の地心緯度と経度。

  • P_l,m — ルジャンドル関数。

  • μ — 中心天体の標準重力パラメータ。

  • R_cb — 中心天体の赤道半径。

  • C_l、m および S_l、m — 正規化されていない高調波係数。

  変換 fixed2inertial は、遠心加速度とコリオリ加速度を考慮して、固定フレームの位置、速度、加速度を中心物体の中心を原点とする ICRF 座標系に変換します。各中心天体に使用される固定座標系と慣性座標系の詳細については、 を参照してください。

大気抵抗

大気抵抗は、地球の大気などの流体中を移動する物体の運動に抵抗する力です。大気の抗力は、物体の形状、大きさ、速度、空気の特性など、いくつかの要因によって影響を受けます。大気抵抗の主なメカニズムは、空気分子の衝突と摩擦のプロセスを通じて物体の運動エネルギーが熱に変換されることです。

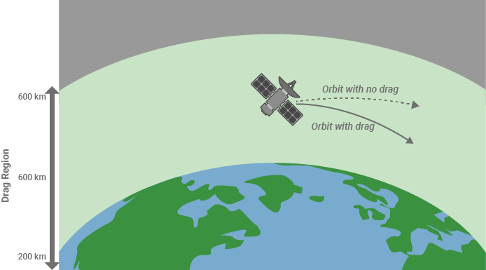
Aerospace Toolbox では、次の大気抵抗方程式が使用されます。

$$a_{drag}=-\frac{1}{2}\rho \left(\frac{C_{D}A}{m}\right)v^2{}_{rel}\frac{{\overrightarrow{v}}_{rel}}{v_{rel}}$$

ここで、

• m — 大気抵抗計算で使用される宇宙機の質量。

• C_D — 無次元であると仮定した抗力係数。

• ρ — 大気の密度。

• A — v_relに垂直な領域。

  $${\overrightarrow{v}}_{rel}={\overrightarrow{v}}_{sat}+{\overrightarrow{v}}_{atmos}$$

• v_rel — 大気に対する速度。

  $${\overrightarrow{v}}_{rel}={\overrightarrow{v}}_{icrf}-{\overrightarrow{\omega }}_{\oplus }\times \overrightarrow{r_{icrf}}$$

  ここで、$${\overrightarrow{\omega }}_{\oplus }$$ は中心物体の角速度です。

第三の体

Aerospace Toolbox では、第 3 の天体 は、重力システム内の 2 つの主要な天体の運動に影響を与える追加の天体を指します。

この方程式には第三物体の寄与が組み込まれており、宇宙における物体の動きをより正確に予測することができます。

$$a_{{}_{third\_body}}={\mu }_{third}\left(\frac{{\overrightarrow{r}}_{sat,3}}{r^3{}_{sat,3}}-\frac{\overrightarrow{r}}{r^3}\right)$$

ここで、

• μ_third — 3 番目の天体の重力パラメータ。

• $${\overrightarrow{r}}_{sat,3}$$ — 衛星から 3 番目の天体へのベクトル。

• $$\overrightarrow{r}$$ — 中心天体に対する 3 番目の天体の位置をベクトルとして指定します。

太陽放射圧

太陽放射圧 (SRP) は、宇宙空間にある物体の表面に太陽光の光子が衝突することによって生じる力です。SRP は、軌道の決定と予測において考慮する必要がある摂動力として考えられています。

Aerospace Toolbox では、次の太陽放射圧方程式を使用します:

$$a_{srp}=-\upsilon C_r\frac{A_s}{m}{P}_{srp}{\left(\frac{AU}{r_{sat,sun}}\right)}^2\frac{{\overrightarrow{r}}_{sat,sun}}{r_{sat,sun}}$$

ここで、

• m — 宇宙機の質量

• v — 日食シャドウ関数

• C_r — 宇宙機の反射係数

• A_s — 宇宙機の太陽放射圧領域

• P_srp — 太陽から AU の距離における太陽放射圧

• AU — 太陽から地球までの平均距離（1AU）

• |$${\overrightarrow{r}}_{{}_{sat,sun}}$$| — 衛星から太陽原点までのベクトル

参考

オブジェクト

• satelliteScenario | access | numericalPropagator | orbit | physicalProperties

関数

• show | play | hide

トピック

• 衛星シナリオのモデル化、可視化、および解析
• 衛星シナリオの重要な概念