メインコンテンツ
Results for
ere's a single MATLAB script addressing all the problems described:
matlab
% Problem 1: Simple if Statement
x = 5; % Example value
if x > 0
disp('The number is positive.');
end
% Problem 2: if ... else Statement
x = 7; % Example value
if mod(x, 2) == 0
disp('The number is even.');
else
disp('The number is odd.');
end
% Problem 3: if ... elseif ... else Statement
score = 85; % Example value
if score >= 90 && score <= 100
disp('Grade A');
elseif score >= 80 && score < 90
disp('Grade B');
elseif score >= 70 && score < 80
disp('Grade C');
elseif score >= 60 && score < 70
disp('Grade D');
else
disp('Grade F');
end
% Problem 4: Nested if Statement
x = 8; % Example value
if x > 0
if mod(x, 2) == 0
disp('The number is positive and even.');
else
disp('The number is positive and odd.');
end
end
% Problem 5: Temperature Classification (if ... elseif)
T = 18; % Example value
if T < 0
disp('Freezing');
elseif T >= 0 && T <= 15
disp('Cold');
elseif T >= 16 && T <= 25
disp('Mild');
else
disp('Hot');
end
% Problem 6: Simple switch Statement
grade = 'B'; % Example value
switch grade
case 'A'
disp('Excellent');
case 'B'
disp('Good');
case 'C'
disp('Fair');
case 'D'
disp('Poor');
case 'F'
disp('Fail');
otherwise
disp('Invalid grade.');
end
% Problem 7: Nested switch Statement
department = 'Engineering'; % Example value
major = 'Mechanical'; % Example value
switch department
case 'Engineering'
switch major
case 'Electrical'
disp('Electrical Engineering');
case 'Mechanical'
disp('Mechanical Engineering');
case 'Civil'
disp('Civil Engineering');
otherwise
disp('Unknown major.');
end
case 'Arts'
disp('Arts Department');
case 'Sciences'
disp('Sciences Department');
otherwise
disp('Unknown department.');
end
% Problem 8: Leap Year Check (if Statements)
year = 2024; % Example value
if mod(year, 4) == 0
if mod(year, 100) ~= 0 || mod(year, 400) == 0
disp('Leap year');
else
disp('Not a leap year');
end
else
disp('Not a leap year');
end
% Problem 9: Triangle Type (if ... elseif)
a = 5; b = 5; c = 5; % Example values
if a == b && b == c
disp('Equilateral triangle');
elseif a == b || b == c || a == c
disp('Isosceles triangle');
else
disp('Scalene triangle');
end
% Problem 10: Calculator with switch Statement
num1 = 10; % Example value
num2 = 5; % Example value
operation = '*'; % Example value
switch operation
case '+'
result = num1 + num2;
disp(['Result: ', num2str(result)]);
case '-'
result = num1 - num2;
disp(['Result: ', num2str(result)]);
case '*'
result = num1 * num2;
disp(['Result: ', num2str(result)]);
case '/'
if num2 ~= 0
result = num1 / num2;
disp(['Result: ', num2str(result)]);
else
disp('Error: Division by zero');
end
otherwise
disp('Invalid operation');
end
This code covers all the problems mentioned in your document. Replace the example values with inputs as needed.
% MATLAB Homework Solutions
% Problem 1: Sum of Even Numbers using while Loop
sum_even = 0;
num = 1;
while num <= 50
if mod(num, 2) == 0
sum_even = sum_even + num;
end
num = num + 1;
end
disp('Problem 1: Sum of Even Numbers');
disp(sum_even);
% Problem 2: Factorial Calculation using for Loop
n = 5; % Example number to calculate factorial
factorial_result = 1;
for i = 1:n
factorial_result = factorial_result * i;
end
disp('Problem 2: Factorial of the number');
disp(factorial_result);
% Problem 3: Multiplication Table using Nested Loops
disp('Problem 3: 10x10 Multiplication Table');
for i = 1:10
for j = 1:10
fprintf('%d\t', i * j);
end
fprintf('\n');
end
% Problem 4: Count Digits using while Loop
number = 12345; % Example number
digit_count = 0;
while number > 0
number = floor(number / 10);
digit_count = digit_count + 1;
end
disp('Problem 4: Number of digits');
disp(digit_count);
% Problem 5: Skip Multiples of 3 using for Loop and continue
disp('Problem 5: Numbers from 1 to 20 (skipping multiples of 3)');
for i = 1:20
if mod(i, 3) == 0
continue;
end
disp(i);
end
% Problem 6: Break a while Loop when Condition is Met
num = 101; % Start checking from 101
while true
if mod(num, 5) == 0 && mod(num, 7) == 0
disp('Problem 6: First number greater than 100 divisible by 5 and 7');
disp(num);
break;
end
num = num + 1;
end
% Problem 7: Summing Diagonal Elements using Nested Loops
matrix = randi([1, 20], 5, 5); % Create a 5x5 random matrix
diagonal_sum = 0;
for i = 1:5
diagonal_sum = diagonal_sum + matrix(i, i);
end
disp('Problem 7: Sum of diagonal elements');
disp(matrix); % Display the matrix
disp(diagonal_sum);
% Problem 8: Reverse a Number using while Loop
num = 12345; % Example number
reversed = 0;
while num > 0
remainder = mod(num, 10);
reversed = reversed * 10 + remainder;
num = floor(num / 10);
end
disp('Problem 8: Reversed number');
disp(reversed);
% Problem 9: Prime Number Checker using for Loop and break
num = 29; % Example number to check
is_prime = true; % Assume the number is prime
if num < 2
is_prime = false;
else
for i = 2:sqrt(num)
if mod(num, i) == 0
is_prime = false;
break;
end
end
end
disp('Problem 9: Is the number prime?');
disp(is_prime);
% Problem 10: Display Pascal's Triangle using Nested Loops
n = 5; % Number of rows in Pascal's Triangle
disp('Problem 10: Pascal''s Triangle');
for i = 0:n-1
row = 1; % First element in the row
for j = 0:i
fprintf('%d ', row);
row = row * (i - j) / (j + 1); % Calculate next element
end
fprintf('\n'); % Move to the next row
end
% MATLAB Homework: Matrix Solutions
%% 1. Create a 5x5 Matrix
A1 = reshape(1:25, 5, 5)'; % 5x5 matrix with elements 1 to 25 arranged row-wise
disp('1. 5x5 Matrix:');
disp(A1);
%% 2. Element Referencing
b = [10 20 30; 40 50 60; 70 80 90];
element = b(3,2); % Element in 3rd row, 2nd column
disp('2. Element Referencing (3rd row, 2nd column):');
disp(element);
%% 3. Column Vector Creation
v = b(:,1); % First column of matrix b
disp('3. Column Vector (1st column of b):');
disp(v);
%% 4. Sub-matrix Extraction
subMatrix = b(2:3, 1:2); % Last two rows, first two columns
disp('4. 2x2 Sub-Matrix:');
disp(subMatrix);
%% 5. Row Deletion
c = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16];
c(2,:) = []; % Delete second row
disp('5. Matrix after Row Deletion:');
disp(c);
%% 6. Column Deletion
c(:,3) = []; % Delete third column
disp('6. Matrix after Column Deletion:');
disp(c);
%% 7. Matrix Addition and Subtraction
d = [1 2 3; 4 5 6; 7 8 9];
e = [9 8 7; 6 5 4; 3 2 1];
addResult = d + e; % Matrix addition
subResult = d - e; % Matrix subtraction
disp('7. Matrix Addition (d + e):');
disp(addResult);
disp('Matrix Subtraction (d - e):');
disp(subResult);
%% 8. Matrix Scalar Operations
scalarMultiply = d * 3; % Multiply by 3
scalarDivide = d / 3; % Divide by 3
disp('8. Matrix after Scalar Multiplication (d * 3):');
disp(scalarMultiply);
disp('Matrix after Scalar Division (d / 3):');
disp(scalarDivide);
%% 9. Matrix Transposition
f = [1 3 5; 2 4 6];
fTranspose = f';
disp('9. Transposed Matrix:');
disp(fTranspose);
%% 10. Matrix Inverse and Determinant
g = [1 0 2; 2 1 3; 3 4 1];
det_g = det(g); % Determinant
disp('10. Determinant of Matrix g:');
disp(det_g);
if det_g ~= 0
gInverse = inv(g); % Inverse of g
disp('Inverse of Matrix g:');
disp(gInverse);
else
disp('Matrix g is singular and does not have an inverse.');
end
%% 11. Dynamic Matrix Creation
n = input('Enter the size of the square matrix n: ');
A_dynamic = zeros(n,n);
for i = 1:n
for j = 1:n
A_dynamic(i,j) = i * j;
end
end
disp('11. Dynamic Square Matrix A (i*j):');
disp(A_dynamic);
%% 12. Checkerboard Matrix
n = 8; % Size of checkerboard matrix
checkerboard = mod((1:n)' + (1:n), 2); % Checkerboard logic
disp('12. Checkerboard Matrix (n=8):');
disp(checkerboard);
%% 13. Rotating a Matrix 90 Degrees Clockwise
M = [1 2 3; 4 5 6; 7 8 9]; % Test matrix
rotatedMatrix = M';
rotatedMatrix = flipud(rotatedMatrix);
disp('13. Rotated Matrix (90 Degrees Clockwise):');
disp(rotatedMatrix);
%% 14. Diagonal Dominance Validator
function isDominant = checkDiagonalDominance(X)
n = size(X, 1);
isDominant = true;
for i = 1:n
if abs(X(i,i)) <= sum(abs(X(i,:))) - abs(X(i,i))
isDominant = false;
break;
end
end
end
% Example: Test the diagonal dominance validator
matrixTest = [3 1 1; 1 4 1; 0 2 5];
disp('14. Diagonal Dominance Check:');
if checkDiagonalDominance(matrixTest)
disp('Matrix is diagonally dominant.');
else
disp('Matrix is NOT diagonally dominant.');
end
%% 15. Matrix Pattern Extraction (Cross Shape)
X = magic(7); % Create a 7x7 test matrix
middleRow = X(ceil(end/2), :);
middleColumn = X(:, ceil(end/2));
crossShape = [middleRow; middleColumn'];
disp('15. Extracted Cross Shape from Center of Matrix:');
disp('Middle Row:');
disp(middleRow);
disp('Middle Column:');
disp(middleColumn);
If you have a folder with an enormous number of files and want to use the uigetfile function to select specific files, you may have noticed a significant delay in displaying the file list.
Thanks to the assistance from MathWorks support, an interesting behavior was observed.
For example, if a folder such as Z:\Folder1\Folder2\data contains approximately 2 million files, and you attempt to use uigetfile to access files with a specific extension (e.g., *.ext), the following behavior occurs:
Method 1: This takes minutes to show me the list of all files
[FileName, PathName] = uigetfile('Z:\Folder1\Folder2\data\*.ext', 'File selection');
Method 2: This takes less than a second to display all files.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data');
Method 3: This method also takes minutes to display the file list. What is intertesting is that this method is the same as Method 2, except that a file seperator "\" is added at the end of the folder string.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data\');
I was informed that the Mathworks development team has been informed of this strange behaviour.
I am using 2023a, but think this should be the same for newer versions.
This post is more of a "tips and tricks" guide than a question.
If you have a folder with an enormous number of files and want to use the uigetfile function to select specific files, you may have noticed a significant delay in displaying the file list.
Thanks to the assistance from MathWorks support, an interesting behavior was observed.
For example, if a folder such as Z:\Folder1\Folder2\data contains approximately 2 million files, and you attempt to use uigetfile to access files with a specific extension (e.g., *.ext), the following behavior occurs:
Method 1: This takes minutes to show me the list of all files
[FileName, PathName] = uigetfile('Z:\Folder1\Folder2\data\*.ext', 'File selection');
Method 2: This takes less than a second to display all files.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data');
Method 3: This method also takes minutes to display the file list. What is intertesting is that this method is the same as Method 2, except that a file seperator "\" is added at the end of the folder string.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data\');
I was informed that the Mathworks development team has been informed of this strange behaviour.
I am using 2023a, but think this should be the same for newer versions.
I'm beginning this MATLAB-based numerical methods class, and as I was thinking back to my previous MATLAB/Simulink classes, I definitely remember some projects more fondly than others. One of my most memorable was where I had to use MATLAB to analyze electrocardiogram (ECG) peaks. What about you guys? What are some of the best (or worst 🤭) MATLAB projects or assignments you've been given in the past?


Christmas is coming, here are two dynamic Christmas tree drawing codes:
Crystal XMas Tree
function XmasTree2024_1
fig = figure('Units','normalized', 'Position',[.1,.1,.5,.8],...
'Color',[0,9,33]/255, 'UserData',40 + [60,65,75,72,0,59,64,57,74,0,63,59,57,0,1,6,45,75,61,74,28,57,76,57,1,1]);
axes('Parent',fig, 'Position',[0,-1/6,1,1+1/3], 'UserData',97 + [18,11,0,13,3,0,17,4,17],...
'XLim',[-1.5,1.5], 'YLim',[-1.5,1.5], 'ZLim',[-.2,3.8], 'DataAspectRatio', [1,1,1], 'NextPlot','add',...
'Projection','perspective', 'Color',[0,9,33]/255, 'XColor','none', 'YColor','none', 'ZColor','none')
%% Draw Christmas tree
F = [1,3,4;1,4,5;1,5,6;1,6,3;...
2,3,4;2,4,5;2,5,6;2,6,3];
dP = @(V) patch('Faces',F, 'Vertices',V, 'FaceColor',[0 71 177]./255,...
'FaceAlpha',rand(1).*0.2+0.1, 'EdgeColor',[0 71 177]./255.*0.8,...
'EdgeAlpha',0.6, 'LineWidth',0.5, 'EdgeLighting','gouraud', 'SpecularStrength',0.3);
r = .1; h = .8;
V0 = [0,0,0; 0,0,1; 0,r,h; r,0,h; 0,-r,h; -r,0,h];
% Rotation matrix
Rx = @(V, theta) V*[1 0 0; 0 cos(theta) sin(theta); 0 -sin(theta) cos(theta)];
Rz = @(V, theta) V*[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0; 0 0 1];
N = 180; Vn = zeros(N, 3); eval(char(fig.UserData))
for i = 1:N
tV = Rz(Rx(V0.*(1.2 - .8.*i./N + rand(1).*.1./i^(1/5)), pi/3.*(1 - .6.*i./N)), i.*pi/8.1 + .001.*i.^2) + [0,0,.016.*i];
dP(tV); Vn(i,:) = tV(2,:);
end
scatter3(Vn(:,1).*1.02,Vn(:,2).*1.02,Vn(:,3).*1.01, 30, 'w', 'Marker','*', 'MarkerEdgeAlpha',.5)
%% Draw Star of Bethlehem
w = .3; R = .62; r = .4; T = (1/8:1/8:(2 - 1/8)).'.*pi;
V8 = [ 0, 0, w; 0, 0,-w;
1, 0, 0; 0, 1, 0; -1, 0, 0; 0,-1,0;
R, R, 0; -R, R, 0; -R,-R, 0; R,-R,0;
cos(T).*r, sin(T).*r, T.*0];
F8 = [1,3,25; 1,3,11; 2,3,25; 2,3,11; 1,7,11; 1,7,13; 2,7,11; 2,7,13;
1,4,13; 1,4,15; 2,4,13; 2,4,15; 1,8,15; 1,8,17; 2,8,15; 2,8,17;
1,5,17; 1,5,19; 2,5,17; 2,5,19; 1,9,19; 1,9,21; 2,9,19; 2,9,21;
1,6,21; 1,6,23; 2,6,21; 2,6,23; 1,10,23; 1,10,25; 2,10,23; 2,10,25];
V8 = Rx(V8.*.3, pi/2) + [0,0,3.5];
patch('Faces',F8, 'Vertices',V8, 'FaceColor',[255,223,153]./255,...
'EdgeColor',[255,223,153]./255, 'FaceAlpha', .2)
%% Draw snow
sXYZ = rand(200,3).*[4,4,5] - [2,2,0];
sHdl1 = plot3(sXYZ(1:90,1),sXYZ(1:90,2),sXYZ(1:90,3), '*', 'Color',[.8,.8,.8]);
sHdl2 = plot3(sXYZ(91:200,1),sXYZ(91:200,2),sXYZ(91:200,3), '.', 'Color',[.6,.6,.6]);
annotation(fig,'textbox',[0,.05,1,.09], 'Color',[1 1 1], 'String','Merry Christmas Matlaber',...
'HorizontalAlignment','center', 'FontWeight','bold', 'FontSize',48,...
'FontName','Times New Roman', 'FontAngle','italic', 'FitBoxToText','off','EdgeColor','none');
% Rotate the Christmas tree and let the snow fall
for i=1:1e8
sXYZ(:,3) = sXYZ(:,3) - [.05.*ones(90,1); .06.*ones(110,1)];
sXYZ(sXYZ(:,3)<0, 3) = sXYZ(sXYZ(:,3) < 0, 3) + 5;
sHdl1.ZData = sXYZ(1:90,3); sHdl2.ZData = sXYZ(91:200,3);
view([i,30]); drawnow; pause(.05)
end
end

Curved XMas Tree
function XmasTree2024_2
fig = figure('Units','normalized', 'Position',[.1,.1,.5,.8],...
'Color',[0,9,33]/255, 'UserData',40 + [60,65,75,72,0,59,64,57,74,0,63,59,57,0,1,6,45,75,61,74,28,57,76,57,1,1]);
axes('Parent',fig, 'Position',[0,-1/6,1,1+1/3], 'UserData',97 + [18,11,0,13,3,0,17,4,17],...
'XLim',[-6,6], 'YLim',[-6,6], 'ZLim',[-16, 1], 'DataAspectRatio', [1,1,1], 'NextPlot','add',...
'Projection','perspective', 'Color',[0,9,33]/255, 'XColor','none', 'YColor','none', 'ZColor','none')
%% Draw Christmas tree
[X,T] = meshgrid(.4:.1:1, 0:pi/50:2*pi);
XM = 1 + sin(8.*T).*.05;
X = X.*XM; R = X.^(3).*(.5 + sin(8.*T).*.02);
dF = @(R, T, X) surf(R.*cos(T), R.*sin(T), -X, 'EdgeColor',[20,107,58]./255,...
'FaceColor', [20,107,58]./255, 'FaceAlpha',.2, 'LineWidth',1);
CList = [254,103,110; 255,191,115; 57,120,164]./255;
for i = 1:5
tR = R.*(2 + i); tT = T+i; tX = X.*(2 + i) + i;
SFHdl = dF(tR, tT, tX);
[~, ind] = sort(SFHdl.ZData(:)); ind = ind(1:8);
C = CList(randi([1,size(CList,1)], [8,1]), :);
scatter3(tR(ind).*cos(tT(ind)), tR(ind).*sin(tT(ind)), -tX(ind), 120, 'filled',...
'CData', C, 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.3)
scatter3(tR(ind).*cos(tT(ind)), tR(ind).*sin(tT(ind)), -tX(ind), 60, 'filled', 'CData', C)
end
%% Draw Star of Bethlehem
Rx = @(V, theta) V*[1 0 0; 0 cos(theta) sin(theta); 0 -sin(theta) cos(theta)];
% Rz = @(V, theta) V*[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0; 0 0 1];
w = .3; R = .62; r = .4; T = (1/8:1/8:(2 - 1/8)).'.*pi;
V8 = [ 0, 0, w; 0, 0,-w;
1, 0, 0; 0, 1, 0; -1, 0, 0; 0,-1,0;
R, R, 0; -R, R, 0; -R,-R, 0; R,-R,0;
cos(T).*r, sin(T).*r, T.*0];
F8 = [1,3,25; 1,3,11; 2,3,25; 2,3,11; 1,7,11; 1,7,13; 2,7,11; 2,7,13;
1,4,13; 1,4,15; 2,4,13; 2,4,15; 1,8,15; 1,8,17; 2,8,15; 2,8,17;
1,5,17; 1,5,19; 2,5,17; 2,5,19; 1,9,19; 1,9,21; 2,9,19; 2,9,21;
1,6,21; 1,6,23; 2,6,21; 2,6,23; 1,10,23; 1,10,25; 2,10,23; 2,10,25];
V8 = Rx(V8.*.8, pi/2) + [0,0,-1.3];
patch('Faces',F8, 'Vertices',V8, 'FaceColor',[255,223,153]./255,...
'EdgeColor',[255,223,153]./255, 'FaceAlpha', .2)
annotation(fig,'textbox',[0,.05,1,.09], 'Color',[1 1 1], 'String','Merry Christmas Matlaber',...
'HorizontalAlignment','center', 'FontWeight','bold', 'FontSize',48,...
'FontName','Times New Roman', 'FontAngle','italic', 'FitBoxToText','off','EdgeColor','none');
%% Draw snow
sXYZ = rand(200,3).*[12,12,17] - [6,6,16];
sHdl1 = plot3(sXYZ(1:90,1),sXYZ(1:90,2),sXYZ(1:90,3), '*', 'Color',[.8,.8,.8]);
sHdl2 = plot3(sXYZ(91:200,1),sXYZ(91:200,2),sXYZ(91:200,3), '.', 'Color',[.6,.6,.6]);
for i=1:1e8
sXYZ(:,3) = sXYZ(:,3) - [.1.*ones(90,1); .12.*ones(110,1)];
sXYZ(sXYZ(:,3)<-16, 3) = sXYZ(sXYZ(:,3) < -16, 3) + 17.5;
sHdl1.ZData = sXYZ(1:90,3); sHdl2.ZData = sXYZ(91:200,3);
view([i,30]); drawnow; pause(.05)
end
end

I wish all MATLABers a Merry Christmas in advance!
Watt's Up with Electric Vehicles?EV modeling Ecosystem (Eco-friendly Vehicles), V2V Communication and V2I communications thereby emitting zero Emissions to considerably reduce NOx ,Particulates matters,CO2 given that Combustion is always incomplete and will always be.
Reduction of gas emissions outside to the environment will improve human life span ,few epidemic diseases and will result in long life standard
Objectif : Etude d'une chaine de transmission numérique avec des turbo-codes combiné avec la technique HARQ (Hybrid Automatic Repeat reQuest):
* Mettre en place une chaîne de transmission numérique avec des turbo codes intégrant la technique HARQ.
* Évaluer les performances de cette chaîne, en termes de taux d'erreur et de débit sous diverses conditions de canal.
En structurant ainsi votre étude, vous pourrez mener une analyse approfondie des turbo codes et de la technique HARQ.
Outils : Utilisez des outils comme MATLAB, Simulink ou Python (avec des bibliothèques comme Scipy pour la modélisation des canaux et NumPy pour la gestion des calculs).
Simulations : Créez une série de simulations en variant les paramètres comme le SNR, le type de HARQ utilisé, etc.
Compétences développées : Maîtrise des techniques de détection et de correction d’erreurs pour améliorer la fiabilité des transmissions
Always and almost immediately!
25%
Never
30%
After validating existing code
16%
Y'all get the new releases?
29%
1288 票
Many of my best friends at MathWorks speak Spanish as their first language and we have a large community of Spanish-speaking users. You can see good evidence of this by checking out our relatively new Spanish YouTube channel which recently crossed the 10,000 subscriber mark
I've always used MATLAB with other languages. In the early days, C and C++ via mex files were the most common ways I spliced two languages together. Other than that I've also used MATLAB with Java, Excel and even Fortran.
In more recent years, Python is the language I tend to use most alongside MATLAB and support for this combination is steadily improving. In my latest blog post, I show how easy it has become to use Python's Numpy with MATLAB.
Have you used this functionality much? If so, what for? How well did it work for you?
MathWorks
Accelerating the pace of engineering and science.
I am inspired by the latest video from YouTube science content creator Veritasium on his distinct yet thorough explanation on how rainbows work. In his video, he set up a glass sphere experiment representing how light rays would travel inside a raindrop that ultimately forms the rainbow. I highly recommend checking it out.
In the meantime, I created an interactive MATLAB App in MATLAB Online using App Designer to visualize the light paths going through a spherical raindrop with numerical calculations along the way. While I've seen many diagrams out there showing the light paths, I haven't found any doing calculations in each step. Hence I created an app in MATLAB to show the calculations along with the visualizations as one varies the position of the incoming light ray.
Demo video:
For more information about the app and how to open it and play around with it in MATLAB Online, please check out my blog article:

The Queen’s MATLAB
Good news for those of you who speak (and spell) the Queen's English instead of the US dialect. We are working night and day to make MATLAB use equally satisfying for the entire world's English speaking population!ContentsExpectations for Upcoming ReleasesNamesOur Current ListHelp Us Out!Expectations for Upcoming ReleasesYou can expect, in upcoming releases, to create a colorbar or a colourbar.
Our MathWorks Usability Team is working on an accessibility project and they want to interview people who use MATLAB and also have experience with screen readers.
If you fit the criteria and are interested, sign up here https://www.mathworks.com/products/usability.html?tfa_30=A11Y
Provide Usability Feedback
Help improve MATLAB and Simulink and the MathWorks web site by participating in a user research session.
I wish I knew more about the intended evolution of the capabilities of the function arguments block. I love implementing function syntaxes using this relatively new form, but it doesn't yet handle some function syntax design patterns that I think are valuable and worth keeping.
For example, some functions take an input quantity that can something numeric, or it can be an option string that descriptively names a particular value of that quantity. One example is dateshift(t,"dayofweek",dow), where dow can be an integer from 1 to 7, or it can be one of the option strings "weekday" or "weekend".
Another example is Image Processing Toolbox that take a connectivity specifier as input. The function bwconncomp is one particular case. Connectivity can be specified using certain scalars, certain arrays, or the option string "maximal".
I think this is a worthwhile function design pattern, but I don't think the arguments block validation functionality supports it well (unless you use a lot of extra code that duplicates standard MATLAB behavior, which undermines the value of the arguments block).
MathWorkers - believe me, I know that it is not in your DNA to discuss future features. But would anyone care to offer a hint about directions for the arguments block functionality?
Hi! My name is Mike McLernon, and I’m a product marketing engineer with MathWorks. In my role, I look at the trends ongoing in the wireless industry, across lots of different standards (think 5G, WLAN, SatCom, Bluetooth, etc.), and I seek to shape and guide the software that MathWorks builds to respond to these trends. That’s all about communicating within the Mathworks organization, but every so often it’s worth communicating these trends to our audience in the world at large. Many of the people reading this are engineers (or engineers at heart), and we all want to know what’s happening in the geek world around us. I think that now is one of these times to communicate an important milestone. So, without further ado . . .
Bluetooth 6.0 is here! Announced in September by the Bluetooth Special Interest Group (SIG), it’s making more advances in its quest to create a “world without wires”. A few of the salient features in Bluetooth 6.0 are:
- Channel sounding (for accurate distance measurements)
- Decision-based advertising filtering (for more efficient channel scanning)
- Monitoring advertisers (for improved energy efficiency when devices come into and go out of range)
- Frame space updates (for both higher throughput and better coexistence management)
Bluetooth 6.0 includes other features as well, but the SIG has put special promotional emphasis on channel sounding (CS), which once upon a time was called High Accuracy Distance Measurement (HADM). The SIG has said that CS is a step towards true distance awareness, and 10 cm ranging accuracy. I think their emphasis is in exactly the right place, so let’s learn more about this technology and how it is used.
CS can be used for the following use cases:
- Keyless vehicle entry, performed by communication between a key fob or phone and the car’s anchor points
- Smart locks, to permit access only when an authorized device is within a designated proximity to the locks
- Geofencing, to limit access to designated areas
- Warehouse management, to monitor inventory and manage logistics
- Asset tracking for virtually any object of interest

In the past, Bluetooth devices would use a received signal strength indicator (RSSI) measurement to infer the distance between two of them. They would assume a free space path loss on the link, and use a straightforward equation to estimate distance:
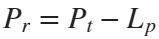
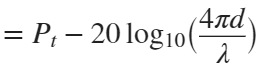
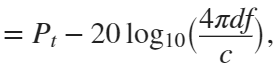 where
whereSo in this method, 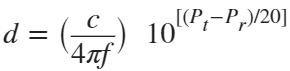 . But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
. But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
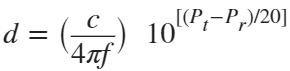 . But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
. But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.Bluetooth 6.0 introduces not one, but two ways to accurately measure distance:
- Round-trip time (RTT) measurement
- Phase-based ranging (PBR) measurement
The RTT measurement method uses the fact that the Bluetooth signal time of flight (TOF) between two devices is half the RTT. It can then accurately compute the distance d as
 , where c is again the speed of light. This method requires accurate measurements of the time of departure (TOD) of the outbound signal from device 1 (the Initiator), time of arrival (TOA) of the outbound signal to device 2 (the Reflector), TOD of the return signal from device 2, and TOA of the return signal to device 1. The diagram below shows the signal paths and the times.
, where c is again the speed of light. This method requires accurate measurements of the time of departure (TOD) of the outbound signal from device 1 (the Initiator), time of arrival (TOA) of the outbound signal to device 2 (the Reflector), TOD of the return signal from device 2, and TOA of the return signal to device 1. The diagram below shows the signal paths and the times.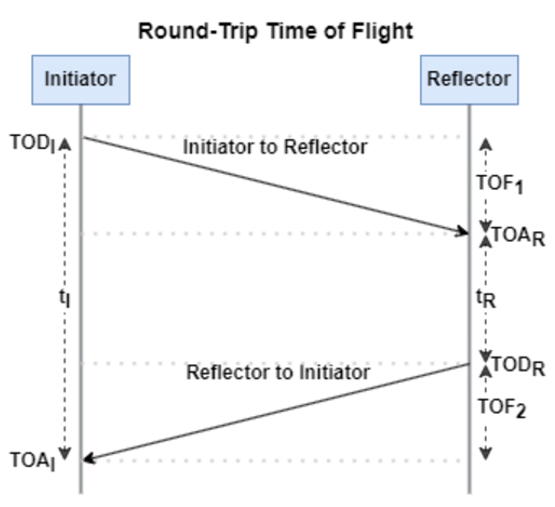
If you want to see how you can use MATLAB to simulate the RTT method, take a look at Estimate Distance Between Bluetooth LE Devices by Using Channel Sounding and Round-Trip Timing.
The PBR method uses two Bluetooth signals of different frequencies to measure distance. These signals are simply tones – sine waves. Without going through the derivation, PBR calculates distance d as
The mod() operation is needed to eliminate ambiguities in the distance calculation and the final division by two is to convert a round trip distance to a one-way distance. Because a given phase difference value can hold true for an infinite number of distance values, the mod() operation chooses the smallest distance that satisfies the equation. Also, these tones can be as close as 1 MHz apart. In that case, the maximum resolvable distance measurement is about 150 m. The plot below shows that ambiguity and repetition in distance measurement.
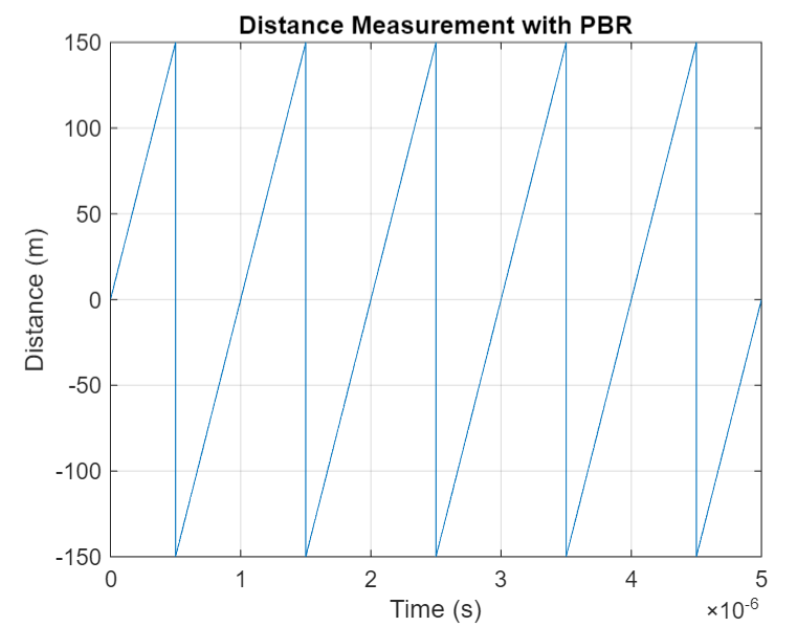
If you want to see how you can use MATLAB to simulate the PBR method, take a look at Estimate Distance Between Bluetooth LE Devices by Using Channel Sounding and Phase-Based Ranging.
Bluetooth 6.0 outlines RTT and PBR distance measurement methods, but CS does not mandate a specific algorithm for calculating distance estimates. This flexibility allows device manufacturers to tailor solutions to various use cases, balancing computational complexity with required accuracy and adapting to different radio environments. Examples include simple phase difference calculations and FFT-based methods.
Although Bluetooth 6.0 is now out, it is far from a finished version. The SIG is actively working through the ratification process for two major extensions:
- High Data Throughput, up to 8 Mbps
- 5 and 6 GHz operation
See the last few minutes of this video from the SIG to learn more about these exciting future developments. And if you want to see more Bluetooth blogs, give a review of this one! Finally, if you have specific Bluetooth questions, give me a shout and let’s start a discussion!
I am very excited to share my new book "Data-driven method for dynamic systems" available through SIAM publishing: https://epubs.siam.org/doi/10.1137/1.9781611978162
This book brings together modern computational tools to provide an accurate understanding of dynamic data. The techniques build on pencil-and-paper mathematical techniques that go back decades and sometimes even centuries. The result is an introduction to state-of-the-art methods that complement, rather than replace, traditional analysis of time-dependent systems. One can find methods in this book that are not found in other books, as well as methods developed exclusively for the book itself. I also provide an example-driven exploration that is (hopefully) appealing to graduate students and researchers who are new to the subject.
Each and every example for the book can be reproduced using the code at this repo: https://github.com/jbramburger/DataDrivenDynSyst
Hope you like it!
Christmas season is underway at my house:

(Sorry - the ornament is not available at the MathWorks Merch Shop -- I made it with a 3-D printer.)
So I made this.

clear
close all
clc
% inspired from: https://www.youtube.com/watch?v=3CuUmy7jX6k
%% user parameters
h = 768;
w = 1024;
N_snowflakes = 50;
%% set figure window
figure(NumberTitle="off", ...
name='Mat-snowfalling-lab (right click to stop)', ...
MenuBar="none")
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
axis equal
axis([0, w, 0, h])
ax.Color = 'k';
ax.XAxis.Visible = 'off';
ax.YAxis.Visible = 'off';
ax.Position = [0, 0, 1, 1];
%% first snowflake
ht = gobjects(1, 1);
for i=1:length(ht)
ht(i) = hgtransform();
ht(i).UserData = snowflake_factory(h, w);
ht(i).Matrix(2, 4) = ht(i).UserData.y;
ht(i).Matrix(1, 4) = ht(i).UserData.x;
im = imagesc(ht(i), ht(i).UserData.img);
im.AlphaData = ht(i).UserData.alpha;
colormap gray
end
%% falling snowflake
tic;
while true
% add a snowflake every 0.3 seconds
if toc > 0.3
if length(ht) < N_snowflakes
ht = [ht; hgtransform()];
ht(end).UserData = snowflake_factory(h, w);
ht(end).Matrix(2, 4) = ht(end).UserData.y;
ht(end).Matrix(1, 4) = ht(end).UserData.x;
im = imagesc(ht(end), ht(end).UserData.img);
im.AlphaData = ht(end).UserData.alpha;
colormap gray
end
tic;
end
ax.CLim = [0, 0.0005]; % prevent from auto clim
% move snowflakes
for i = 1:length(ht)
ht(i).Matrix(2, 4) = ht(i).Matrix(2, 4) + ht(i).UserData.velocity;
end
if strcmp(get(gcf, 'SelectionType'), 'alt')
set(gcf, 'SelectionType', 'normal')
break
end
drawnow
% delete the snowflakes outside the window
for i = length(ht):-1:1
if ht(i).Matrix(2, 4) < -length(ht(i).Children.CData)
delete(ht(i))
ht(i) = [];
end
end
end
%% snowflake factory
function snowflake = snowflake_factory(h, w)
radius = round(rand*h/3 + 10);
sigma = radius/6;
snowflake.velocity = -rand*0.5 - 0.1;
snowflake.x = rand*w;
snowflake.y = h - radius/3;
snowflake.img = fspecial('gaussian', [radius, radius], sigma);
snowflake.alpha = snowflake.img/max(max(snowflake.img));
end
Is it possible to differenciate the input, output and in-between wires by colors?