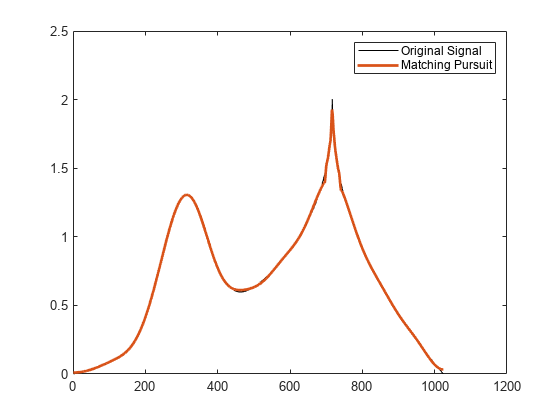
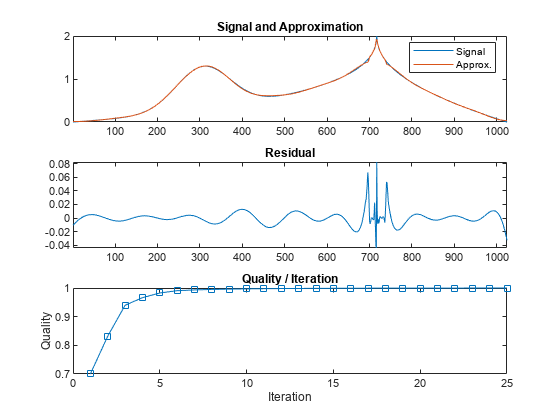
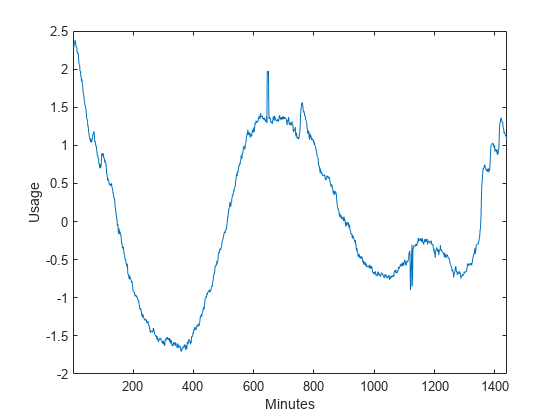
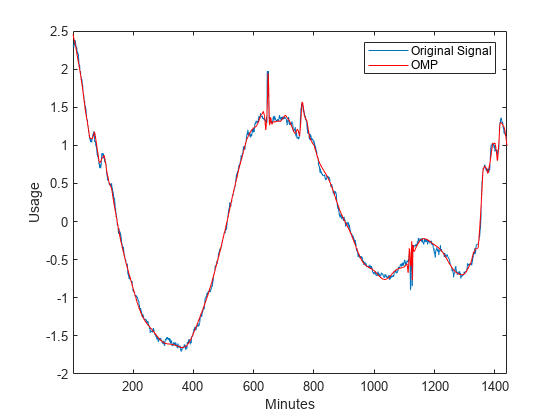
wmpalg
(Not recommended) Matching pursuit
The wmpalg function no longer supports plotting and is no longer
recommended. See Version History.
Syntax
Description
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Cai, T. Tony, and Lie Wang. “Orthogonal Matching Pursuit for Sparse Signal Recovery With Noise.” IEEE Transactions on Information Theory 57, no. 7 (July 2011): 4680–88. https://doi.org/10.1109/TIT.2011.2146090.
[2] Donoho, D.L., M. Elad, and V.N. Temlyakov. “Stable Recovery of Sparse Overcomplete Representations in the Presence of Noise.” IEEE Transactions on Information Theory 52, no. 1 (January 2006): 6–18. https://doi.org/10.1109/TIT.2005.860430.
[3] Mallat, S.G. and Zhifeng Zhang. “Matching Pursuits with Time-Frequency Dictionaries.” IEEE Transactions on Signal Processing 41, no. 12 (December 1993): 3397–3415. https://doi.org/10.1109/78.258082.
[4] Tropp, J.A. “Greed Is Good: Algorithmic Results for Sparse Approximation.” IEEE Transactions on Information Theory 50, no. 10 (October 2004): 2231–42. https://doi.org/10.1109/TIT.2004.834793.