このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

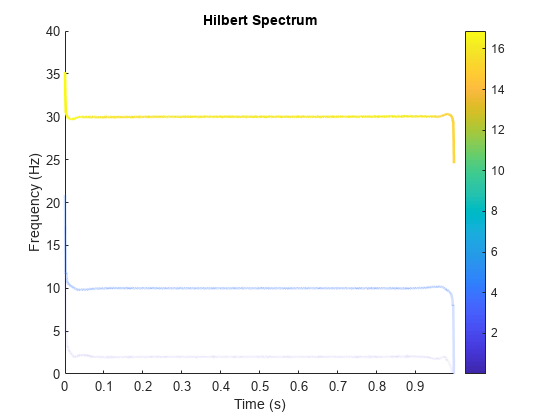
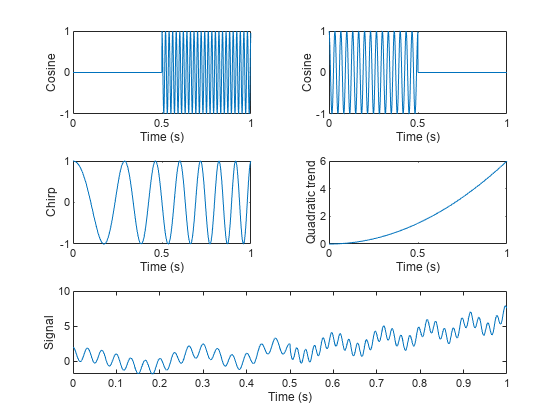
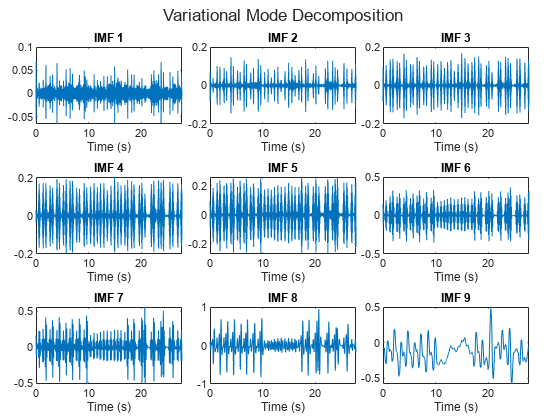
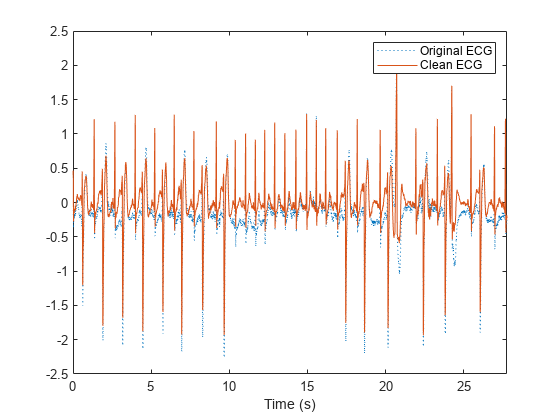
vmd

変分的モード分解

R2020a 以降

構文

imf = vmd(x)

[imf,residual] = vmd(x)

[imf,residual,info] = vmd(x)

[___] = vmd(x,Name=Value)

vmd(___)

説明

imf = vmd(x) は x の変分的モード分解を返します。vmd を使用して、複雑な信号をヒルベルト スペクトル解析に必要な有限数の固有モード関数 (IMF) に分解して単純化します。

[imf,residual] = vmd(x) も x の変分的モード分解に対応する残差信号 residual を返します。

[imf,residual,info] = vmd(x) は、診断の目的のために IMF の追加情報 info と残差信号を返します。

[___] = vmd(x,Name=Value) では、1 つ以上の名前と値の引数で指定された追加オプションを使用して、変分的モード分解を実行します。

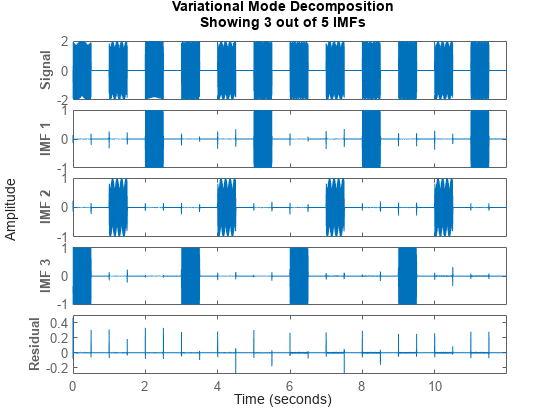
vmd(___) では、同じ Figure 内で元の信号、IMF、残差信号をサブプロットとしてプロットします。

例

ダイヤル トーン信号の変分的モード分解

4 kHz でサンプリングされた信号を作成します。これはデジタル電話のすべてのキーをダイヤルした場合と似ています。信号を MATLAB® の timetable として保存します。

fs = 4e3;
t = 0:1/fs:0.5-1/fs;

ver = [697 770 852 941];
hor = [1209 1336 1477];

tones = [];

for k = 1:length(ver)
    for l = 1:length(hor)
        tone = sum(sin(2*pi*[ver(k);hor(l)].*t))';
        tones = [tones;tone;zeros(size(tone))];
    end
end

% To hear, type soundsc(tones,fs)

S = timetable(tones,'SampleRate',fs);

timetable の変分的モード分解をプロットします。

vmd(S)

多成分信号の VMD

周波数 2 Hz、10 Hz、および 30 Hz の 3 つの正弦波からなる多成分信号を生成します。正弦波は 1 kHz で 2 秒間サンプリングされます。分散 0.01² のホワイト ガウス ノイズに信号を組み込みます。

fs = 1e3;
t = 1:1/fs:2-1/fs;
x = cos(2*pi*2*t) + ...
    2*cos(2*pi*10*t) + ...
    4*cos(2*pi*30*t) + ...
    0.01*randn(1,length(t));

ノイズ信号の IMF を計算し、それを 3 次元プロットで可視化します。

imf = vmd(x);
[p,q] = ndgrid(t,1:size(imf,2));
plot3(p,q,imf)
grid on
xlabel('Time Values')
ylabel('Mode Number')
zlabel('Mode Amplitude')

計算された IMF を使用して、多成分信号のヒルベルト スペクトルをプロットします。周波数範囲を [0, 40] Hz に制限します。

hht(imf,fs,'FrequencyLimits',[0,40])

区分信号の VMD

二次トレンド、チャープ、および t = 0.5 で 2 つの一定周波数間に急峻な遷移をもつ余弦波で構成される、区分合成信号を生成します。

$$\mathit{x}\left(\mathit{t}\right)=6{\mathit{t}}^2+\cos \left(4\pi \mathit{t}+10\pi {\mathit{t}}^2\right)+\{\begin{array}{ll}\cos \left(60\pi \mathit{t}\right),& \mathit{t}\le 0.5,\\ \cos \left(100\pi \mathit{t}-10\pi \right),& \mathit{t}>0.5.\end{array}$$

信号は 1 kHz で 1 秒間サンプリングされます。個々の成分と合成信号をプロットします。

fs = 1e3;
t = 0:1/fs:1-1/fs;

x = 6*t.^2 + cos(4*pi*t+10*pi*t.^2) + ...
    [cos(60*pi*(t(t<=0.5))) cos(100*pi*(t(t>0.5)-10*pi))];

tiledlayout('flow')
nexttile
plot(t,[zeros(1,length(t)/2) cos(100*pi*(t(length(t)/2+1:end))-10*pi)])
xlabel('Time (s)')
ylabel('Cosine')

nexttile
plot(t,[cos(60*pi*(t(1:length(t)/2))) zeros(1,length(t)/2)])
xlabel('Time (s)')
ylabel('Cosine')

nexttile
plot(t,cos(4*pi*t+10*pi*t.^2))
xlabel('Time (s)')
ylabel('Chirp')


nexttile
plot(t,6*t.^2)
xlabel('Time (s)')
ylabel('Quadratic trend')

nexttile(5,[1 2])
plot(t,x)
xlabel('Time (s)')
ylabel('Signal')

変分的モード分解を実行して、4 つの固有モード関数を計算します。信号がもつ 4 つの異なる成分が復元されます。

[imf,res] = vmd(x,'NumIMFs',4);

tiledlayout('flow')

for i = 1:4
    nexttile
    plot(t,imf(:,i))
    txt = ['IMF',num2str(i)];
    ylabel(txt)
    xlabel('Time (s)')
    grid on
end

モード関数と残差を加算することにより、信号を再構成します。元の信号と再構成後の信号をプロットして比較します。

sig = sum(imf,2) + res;

nexttile(5,[1 2])
plot(t,sig,'LineWidth',1.5)

hold on

plot(t,x,':','LineWidth',2)
xlabel('Time (s)')
ylabel('Signal')
hold off
legend('Reconstructed signal','Original signal', ...
       'Location','northwest')

元の信号と再構成後の信号の差のノルムを計算します。

norm(x-sig',Inf)

ans = 0

VMD を使用した ECG 信号からのノイズ除去

MIT-BIH Arrhythmia Database[3] (Signal Processing Toolbox)の Record 200 に対応する信号を読み込みます。信号は 360 Hz でサンプリングされました。信号をプロットします。

load mit200

plot(tm,ecgsig)
xlabel("Time (s)")
xlim([tm(1) tm(end)])

ECG 信号には、心拍リズムおよび振動する低周波パターンが生み出すスパイクが含まれます。ECG の個々のスパイクによって、重要な高次の高調波が引き起こされます。

ウィンドウを適用された信号の 9 つの固有モード関数を計算します。IMF を可視化します。

[imf,residual] = vmd(ecgsig,NumIMFs=9);

t = tiledlayout(3,3, ...
    TileSpacing="compact",Padding="compact");
for n = 1:9
    nexttile(t)
    plot(tm,imf(:,n))
    xlim([tm(1) tm(end)])
    title("IMF "+n)
    xlabel("Time (s)")
end
title(t,"Variational Mode Decomposition")

最初の VMD モード (高周波ノイズの大部分が含まれる) と最後の VMD モード (低周波ベースライン振動が含まれる) を除いたすべての VMD モードを合計することによって、クリーンな ECG 信号を構築します。

cleanECG = sum(imf(:,2:8),2);

figure
plot(tm,ecgsig,":",tm,cleanECG)
legend("Original ECG","Clean ECG")
xlabel("Time (s)")
xlim([tm(1) tm(end)])

入力引数

x — 等間隔でサンプリングされた時間領域信号

ベクトル | timetable

等間隔でサンプリングされた時間領域信号。ベクトルまたは timetable として指定します。x が timetable の場合、増加する有限の行時間を含んでいなければなりません。timetable には、有限の負荷値をもつ数値データ ベクトルを 1 つのみ含めなければなりません。

メモ

timetable が欠損している場合や時間点が重複している場合、欠損または重複する時間および非等間隔の時間をもつ timetable の整理のヒントを使用して修正できます。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: 'NumIMFs',10

AbsoluteTolerance — モード収束絶対許容誤差

5e-6 (既定値) | 正の実数のスカラー

モード収束絶対許容誤差。正の実数スカラーとして指定します。AbsoluteTolerance は最適化の停止条件の 1 つです。つまり、IMF の収束に向けた平均二乗の絶対的改善が 2 つの連続する反復において AbsoluteTolerance 未満となった場合に、最適化が停止します。

RelativeTolerance — モード収束相対許容誤差

AbsoluteTolerance*1e3 (既定値) | 正の実数のスカラー

モード収束相対許容誤差。正の実数スカラーとして指定します。RelativeTolerance は最適化の停止条件の 1 つです。つまり、IMF の収束に向けた平均の相対的改善が 2 つの連続する反復において RelativeTolerance 未満となった場合に、最適化が停止します。

メモ

最適化プロセスは、AbsoluteTolerance と RelativeTolerance が一緒に達成された場合に停止します。

MaxIterations — 最適化の最大反復回数

500 (既定値) | 正のスカラー整数

最適化の最大反復回数。正のスカラー整数として指定します。MaxIterations は最適化の停止条件の 1 つです。つまり、反復回数が MaxIterations より大きくなった場合に、最適化が停止します。

MaxIterations は 0 または正の整数のみを使用して指定できます。

NumIMFs — 抽出された IMF の数

5 (既定値) | 正のスカラー整数

抽出された IMF の数。正のスカラー整数として指定します。

CentralFrequencies — 初期中心 IMF 周波数

ベクトル

初期中心 IMF 周波数。長さ NumIMFs のベクトルとして指定します。ベクトル値は [0, 0.5] サイクル/サンプル内でなければなりません。これは、真の周波数が [0, f_s/2] 内にあることを示します。ここで、f_s はサンプル レートです。

InitialIMFs — 初期 IMF

ゼロ行列 (既定値) | 実数行列

初期 IMF。実数行列として指定します。行は時間サンプルに対応し、列はモードに対応します。

PenaltyFactor — ペナルティ係数

1000 (既定値) | 正の実数のスカラー

ペナルティ係数。正の実数のスカラーとして指定します。この引数により、再構成の忠実度が決まります。より厳しいデータ忠実度を得るには、ペナルティ係数の値を小さくします。

InitialLM — 初期ラグランジュ乗数

ゼロの複素数ベクトル (既定値) | 複素数ベクトル

初期ラグランジュ乗数。複素数ベクトルとして指定します。周波数領域における初期ラグランジュ乗数の範囲は、[0, 0.5] サイクル/サンプルです。この乗数は、再構成時に制約を設けます。乗数の長さは入力サイズに応じて異なります。

LMUpdateRate — ラグランジュ乗数の更新頻度

0.01 (既定値) | 実数スカラー

各反復におけるラグランジュ乗数の更新頻度。正の実数スカラーとして指定します。頻度が増せば収束は高速化しますが、最適化プロセスが局所的最適値で停止する可能性が高まります。

InitializeMethod — 中心周波数の初期化方法

"peaks" (既定値) | "random" | "grid"

中心周波数の初期化方法。"peaks"、"random" または "grid" として指定します。

• "peaks" — 周波数領域における信号のピーク位置として中心周波数を初期化します (既定)。NumIMFs (Signal Processing Toolbox) が周波数領域のピークの数より大きい場合、vmd は残りの中心周波数をランダムに初期化します。

• "random" — 区間 [0,0.5] サイクル/サンプルで一様分布した乱数として中心周波数を初期化します。

• "grid" — 区間 [0,0.5] サイクル/サンプルで等間隔でサンプリングされたグリッドとして中心周波数を初期化します。

Display — コマンド ウィンドウの進行状況表示の切り替え

false または 0 (既定値) | true または 1

コマンド ウィンドウの進行状況表示の切り替え。"true" (もしくは 1) または "false" (もしくは 0) として指定します。"true" を指定した場合、この関数は、モードの平均の絶対的および相対的な改善と 20 回の反復ごとの中心周波数を表示し、最後の停止情報を示します。

テーブルを表示するには Display に 1 を、非表示にするには 0 を指定します。

出力引数

imf — 固有モード関数

行列 | timetable

固有モード関数。行列または timetable として返されます。各 imf は振幅変調および周波数変調された信号で、包絡線は正でゆっくりと変化します。各モードは、非減少で緩やかに変化し、中央値付近に集中する瞬時周波数をもちます。imf を使用してヒルベルト・ファン変換を適用し信号のスペクトル解析を実行します。

imf は以下として返されます。

• x がベクトルの場合、各列が imf の行列。

• x が単一データ列の timetable の場合、timetable。

residual — 残差信号

列ベクトル | 単一データ列 timetable

残差信号。列ベクトルまたは単一データ列の timetable として返されます。residual は vmd によって分解されていない元の信号 x の部分を表します。

residual は以下として返されます。

• x がベクトルの場合、列ベクトル

• x が単一データ列の timetable の場合、単一データ列の timetable

info — 診断の詳細

構造体

診断の詳細。次のフィールドがある構造体として返されます。

• ExitFlag – 終了フラグ。値が 0 であれば、最大反復回数に到達してアルゴリズムが停止したことを示します。値が 1 であれば、絶対許容誤差および相対許容誤差を満たしてアルゴリズムが停止したことを示します。

• CentralFrequencies – IMF の中心周波数。

• NumIterations – 合計反復回数。

• AbsoluteImprovement – 最後の 2 回の反復間における IMF の収束に向けた平均二乗の絶対的改善。

• RelativeImprovement – 最後の 2 回の反復間における IMF の収束に向けた平均の相対的改善。

• LagrangeMultiplier – 最後の反復における周波数領域ラグランジュ乗数。

詳細

固有モード関数

関数 vmd は、信号 x(t) を K 個の少数の狭帯域 "固有モード関数" (IMF) に分解します。

$$x(t)={\displaystyle \sum _{k=1}^K{u}_k(t)}.$$

IMF は次の特性をもちます。

1. 各モード u_k は、次の形式をもつ振幅変調および周波数変調された信号です。

   $$u_k(t)=A_k(t)\cos ({\varphi }_k(t)),$$

   ここで、ϕ_k(t) はモードの位相であり、A_k(t) はその包絡線です。

2. モードは、正でゆっくりと変化する包絡線をもちます。

3. 各モードは、非減少で緩やかに変化し、中央値 f_k 付近に集中する瞬時周波数 ϕ'_k(t) をもちます。

変分的モード分解法では、すべてのモード波形とその中心周波数を同時に計算します。このプロセスは、制約のある変分の問題を最小化する u_k(t) と f_k(t) のセットを見つけることで構成されています。

最適化

u_k と f_k を計算するために、この手続きでは、次の最適な拡張ラグランジュ関数を見つけます。

$$\begin{array}{ccccccc}L(u_k(t),f_k,\lambda (t))& =& \alpha {\displaystyle \sum _{k=1}^K{\Vert \frac{d}{dt}\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast u_k(t)\right]e^{-j2\pi f_{k}t}\Vert }_2^2}& +& {\Vert x(t)-{\displaystyle \sum _{k=1}^K{u}_k(t)}\Vert }_2^2& +& \langle \lambda (t),x(t)-{\displaystyle \sum _{k=1}^K{u}_k(t)}\rangle \\ & & (i)& & (ii)& & (iii)\end{array},$$

ここで、内積 $$\langle p(t),q(t)\rangle ={\displaystyle {\int }_{-\infty }^{\infty }{p}^{\ast }}(t)q(t)dt$$ かつ 2 ノルム $${\Vert p(t)\Vert }_2^2=\langle p(t),p(t)\rangle$$ です。正則化項 (i) には以下のステップが含まれます。

1. ヒルベルト変換を使用して、各モードに関連する解析信号を計算します。ここで、* は畳み込みを表します。その結果、各モードは純粋に正のスペクトルをもちます。

2. 解析信号を複素指数と乗算してベースバンドに復調します。

3. 復調した解析信号がもつ勾配の 2 ノルムの二乗を計算することにより、帯域幅を推定します。

項 (ii) および (iii) は、二次ペナルティを適用し、ラグランジュ乗数を組み込むことにより、制約 $$x(t)={\displaystyle {\sum }_{k=1}^K{u}_k(t)}$$ を適用します。PenaltyFactor α は、(ii) および (iii) と比較した (i) の相対的な重要度を測定します。

このアルゴリズムは、[1] (Signal Processing Toolbox)で説明されている乗数の交互方向法を使用して、最適化問題を解決します。

アルゴリズム

関数 vmd は周波数領域の IMF を計算し、U_k(f) = DFT{u_k(t)} により X(f) = DFT{x(t)} を再構成します。エッジの影響を除去するために、このアルゴリズムでは、信号のどちらかの側の長さを半分にミラーリングすることにより、その信号を拡張します。

最適化 (Signal Processing Toolbox)で紹介したラグランジュ乗数は、フーリエ変換 Ʌ(f) をもちます。ラグランジュ乗数ベクトルの長さは、拡張後の信号の長さになります。

InitialIMFs で特に指定されない限り、IMF はゼロに初期化されます。InitializeMethod で指定した方法のいずれかを使用して CentralFrequencies を初期化します。vmd は、以下の条件のいずれかが達成されるまで、モードを反復的に更新します。

• $${\displaystyle \sum _k{\Vert u_k^{n+1}(t)-u_k^n(t)\Vert }_2^2/{\Vert u_k^n(t)\Vert }_2^2}<{\epsilon }_{\text{r}}$$ および $${\displaystyle \sum _k{\Vert u_k^{n+1}(t)-u_k^n(t)\Vert }_2^2}<{\epsilon }_{\text{a}}$$ が一緒に達成される。ここで、ε_r および ε_a は、それぞれ RelativeTolerance および AbsoluteTolerance を使用して指定されます。

• アルゴリズムが、MaxIterations で指定した最大反復回数を超える。

(n + 1) 回目の反復の場合、アルゴリズムは次のステップを実行します。

1. 次を計算するために、(NumIMFs を使用して指定された) 信号の K 個のモードを反復します。

   1. 次を使用して求めた、各モードの周波数領域波形。

      $$U_k^{n+1}(f)=\frac{X(f)-{\displaystyle \sum _{i<k}{U}_k^{n+1}(f)}-{\displaystyle \sum _{i>k}{U}_k^n}(f)+\frac{{\Lambda }^n}{2}(f)}{1+2\alpha {\{2\pi (f-f_k^n)\}}^2},$$

      ここで、$$U_k^{n+1}(f)$$ は、(n + 1) 回目の反復で計算された k 番目のモードのフーリエ変換です。

   2. 次を使用して求めた、k 番目の中心周波数 $$f_k^{n+1}$$。

      $$f_k^{n+1}=\frac{{\displaystyle {\int }_0^{\infty }{\left|U_k^{n+1}(f)\right|}^{2}f}df}{{\displaystyle {\int }_0^{\infty }{\left|U_k^{n+1}(f)\right|}^2}df}\approx \frac{{\displaystyle \sum f{\left|U_k^{n+1}(f)\right|}^2}}{{\displaystyle \sum {\left|U_k^{n+1}(f)\right|}^2}}.$$

2. $${\Lambda }^{n+1}(f)={\Lambda }^n(f)+\tau (X(f)-{\displaystyle \sum _k{U}_k^{n+1}(f)}),$$ を使用してラグランジュ乗数を更新します。ここで、τ は、LMUpdateRate を使用して指定される、ラグランジュ乗数の更新頻度です。

参照

[1] Boyd, Stephen, Neal Parikh, Eric Chu, Borja Peleato, and Jonathan Eckstein. "Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers." Foundations and Trends^® in Machine Learning. Vol 3, Number 1, 2011, pp. 1–122.

[2] Dragomiretskiy, Konstantin, and Dominique Zosso. "Variational Mode Decomposition." IEEE^® Transactions on Signal Processing. Vol. 62, Number 3, 2014, pp. 531–534.

[3] Moody, George B., and Roger G. Mark. "The impact of the MIT-BIH Arrhythmia Database." IEEE Engineering in Medicine and Biology Magazine. Vol. 20, No. 3, May–June 2001, pp. 45–50.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• x が timetable である場合、オプションの入力 NumIMFs は定数でなければなりません。

バージョン履歴

R2020a で導入

参考

アプリ

• 信号多重解像度アナライザー

関数

• hht | emd

トピック

• 時間-周波数ギャラリー