latex

シンボリック式の LaTeX 形式

構文

chr = latex(S)

説明

chr = latex(S) は、シンボリック式 S の LaTeX 形式を返します。

例

シンボリック式の LaTeX 形式

シンボリック式 x^2 + 1/x と sin(pi*x) + phi の LaTeX 形式を求めます。

syms x phi
chr = latex(x^2 + 1/x)

chr = 
'\frac{1}{x}+x^2'

chr = latex(sin(pi*x) + phi)

chr = 
'\phi +\sin\left(\pi \,x\right)'

シンボリック配列の LaTeX 形式

シンボリック配列 S の LaTeX 形式を求めます。

syms x
S = [sym(1)/3 x; exp(x) x^2]

S = 
$$\left(\begin{array}{cc}\frac{1}{3}& x\\ {\mathrm{e}}^x& x^2\end{array}\right)$$

chr = latex(S)

chr = 
'\left(\begin{array}{cc} \frac{1}{3} & x\\ {\mathrm{e}}^x & x^2 \end{array}\right)'

シンボリック行列変数の LaTeX 形式

いくつかのシンボリック行列変数を使用して計算を実行し、その LaTeX 形式を求めます。

3 行 3 列および 3 行 1 列のシンボリック行列変数を作成します。

syms A 3 matrix
syms X [3 1] matrix

$$X^{T}AX$$ のヘッセ行列を求めます。シンボリック行列変数を含む導出された方程式は、教科書で示されるように、整形されて表示されます。

f = X.'*A*X

f = $$X^{\mathrm{T}}\hspace{0.17em}A\hspace{0.17em}X$$

H = diff(f,X,X.')

H = $$A^{\mathrm{T}}+A$$

シンボリック行列変数 f および H の LaTeX 形式を生成します。

chrf = latex(f)

chrf = 
'{\textbf{X}}^{\mathrm{T}}\,\textbf{A}\,\textbf{X}'

chrH = latex(H)

chrH = 
'{\textbf{A}}^{\mathrm{T}}+\textbf{A}'

シンボリック行列関数の LaTeX 形式

シンボリック行列関数を使用して計算を実行し、その LaTeX 形式を求めます。

3 行 1 列のシンボリック行列変数を作成します。

syms X [3 1] matrix

式 $\mathit{f}\left(\mathit{X}\right)={\mathit{X}}^{\mathit{T}}\mathit{X}$ を表すシンボリック行列関数を作成します。

syms f(X) [1 1] matrix keepargs
f(X) = X.'*X

f(X) = $$X^{\mathrm{T}}\hspace{0.17em}X$$

$\mathit{X}$ について $\mathit{f}\left(\mathit{X}\right)$ の導関数を求めます。

Df = diff(f,X)

Df(X) = $$2\hspace{0.17em}{X}^{\mathrm{T}}$$

シンボリック行列関数 f と Df の LaTeX 形式を生成します。

chrf = latex(f)

chrf = 
'{\textbf{X}}^{\mathrm{T}}\,\textbf{X}'

chrDf = latex(Df)

chrDf = 
'2\,{\textbf{X}}^{\mathrm{T}}'

生成された LaTeX のシンボリック基本設定による変更

生成された LaTeX を、関数symprefを使用してシンボリック基本設定を設定することにより変更します。

式 $$\pi$$ の LaTeX 形式を、既定のシンボリック基本設定で生成します。

sympref("default");
chr = latex(sym(pi))

chr = 
'\pi '

"FloatingPointOutput" 基本設定を true に設定してシンボリック出力を浮動小数点形式で返します。$$\pi$$ の LaTeX 形式を浮動小数点形式で生成します。

sympref("FloatingPointOutput",true);
chr = latex(sym(pi))

chr = 
'3.1416'

ここで、シンボリック多項式の出力順序を変更します。シンボリック多項式を作成し、"PolynomialDisplayStyle" 基本設定を "ascend" に設定します。多項式を昇順に並べ替えた LaTeX 形式を生成します。

syms x;
poly = x^2 - 2*x + 1;
sympref("PolynomialDisplayStyle","ascend");
chr = latex(poly)

chr = 
'1-2\,x+x^2'

sympref を使用して設定した基本設定は、現在およびこれ以降の MATLAB® セッションを通じて維持されます。既定値に戻すには "default" オプションを指定します。

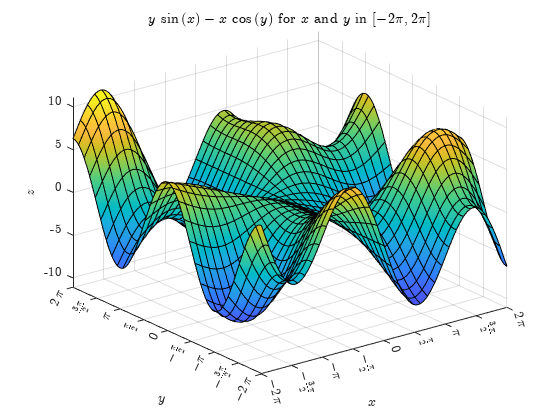
sympref("default");

LaTeX を使用したタイトル、座標軸ラベルおよび目盛りの書式設定

$$x$$ と $$y$$ について $$-2\pi$$ から $$2\pi$$ まで、3 次元表面 $$y\sin (x)-x\cos (y)$$ をプロットします。gca を使用して a に axes オブジェクトを格納します。目盛りラベルには latex インタープリターを使用します。

$$x$$ 軸の範囲を pi/2 の間隔にして、$$x$$ 軸の目盛りを作成します。round を使用して座標軸の範囲を pi/2 の倍数に正確に変換し、S の目盛りのシンボリックな値を取得します。関数 xticks を使用して、$$x$$ 軸の目盛の位置を設定します。arrayfun を使用して latex を S に適用した後に、$ を連結して、$$x$$ 軸の LaTeX ラベルを作成します。関数 xticklabels を使用して、このラベルを表示します。

以上の手順を、$$y$$ 軸について繰り返します。latex インタープリターを使用して $$x$$ 軸と $$y$$ 軸のラベルおよびタイトルを設定します。

syms x y
f = y*sin(x)-x*cos(y);
fsurf(f,[-2*pi 2*pi])
a = gca;
a.TickLabelInterpreter = "latex";

S = sym(a.XLim(1):pi/2:a.XLim(2));
S = sym(round(S/pi*2)*pi/2);
xticks(double(S));
labels = "$" + arrayfun(@latex,S,UniformOutput=false) + "$";
xticklabels(labels);

S = sym(a.YLim(1):pi/2:a.YLim(2));
S = sym(round(S/pi*2)*pi/2);
yticks(double(S))
labels = "$" + arrayfun(@latex,S,UniformOutput=false) + "$";
yticklabels(labels);

xlabel("$x$",Interpreter="latex");
ylabel("$y$",Interpreter="latex");
zlabel("$z$",Interpreter="latex");
titletext = "$" + latex(f) + "$ for $x$ and $y$ in $[-2\pi,2\pi]$";
title(titletext,Interpreter="latex")

入力引数

S — 入力

シンボリック数 | シンボリック変数 | シンボリック ベクトル | シンボリック配列 | シンボリック関数 | シンボリック式 | シンボリック行列変数 | シンボリック行列関数

入力。シンボリック数、シンボリック変数、シンボリック ベクトル、シンボリック配列、シンボリック関数、シンボリック式、シンボリック行列変数、またはシンボリック行列関数として指定します。

データ型: sym | symfun | symmatrix | symfunmatrix

バージョン履歴

R2006a より前に導入

R2022a: シンボリック行列関数の LaTeX 形式の生成

関数 latex は symfunmatrix 型の入力引数を受け入れます。例については、シンボリック行列関数の LaTeX 形式を参照してください。

R2021b: シンボリック行列変数の LaTeX 形式の生成

関数 latex は symmatrix 型の入力引数を受け入れます。例については、シンボリック行列変数の LaTeX 形式を参照してください。

参考

ccode | displayFormula | fortran | texlabel | mathml | sympref

トピック

• ライブ エディターにおけるシンボリック出力のコピーと貼り付け