陰関数表面の接平面と法線

R2021b 以降

この例では、陰関数表面の接平面と法線を求める方法を示します。この例では、コンパクトな数学的表記のために、シンボリック行列変数 (symmatrixデータ型) を使用します。

表面は、球体 $x^{2} + y^{2} + z^{2} = R^{2}$ のように暗黙的に定義できます。一般に、暗黙的に定義された曲面は、 $f (x, y, z) = k$ という方程式で表されます。この例では、半径が $R = \sqrt{14}$ の球体の接平面と法線を求めます。

シンボリック行列変数 $r$ を作成して、 $⟨ x, y, z ⟩$ 座標を表します。球面関数を $f (r) = r \cdot r$ として定義します。

clear; close all; clc
syms r [1 3] matrix
f = r*r.'

f =  $r r^{T}$

陰的方程式 $f (r) = 14$ は、球体を表します。symmatrix2symを使用して、方程式を syms データ型に変換します。関数fimplicit3を使用して方程式をプロットします。

feqn = symmatrix2sym(f == 14)

feqn =  ${r_{1, 1}}^{2} + {r_{1, 2}}^{2} + {r_{1, 3}}^{2} = 14$

fimplicit3(feqn)
axis equal
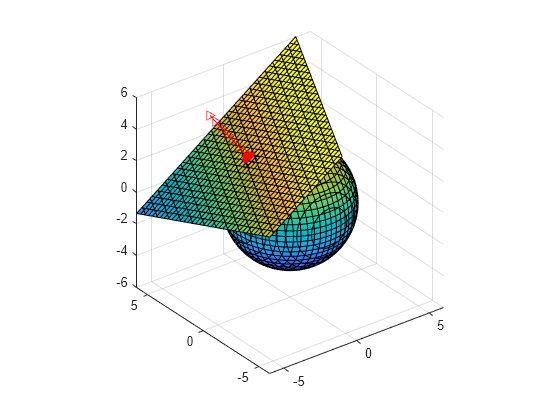
axis([-6 6 -6 6 -6 6])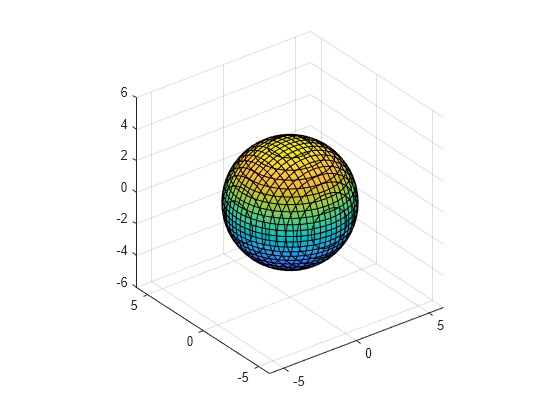

次に、点 $r_{0} = ⟨ x_{0}, y_{0}, z_{0} ⟩$ における接平面と法線を求めます。

$f$ の勾配ベクトルが $\nabla f (r) = ⟨ f_{x} (r), f_{y} (r), f_{z} (r) ⟩$ であることを思い出してください。このとき、点 $r_{0}$ における接平面の方程式は、 $f_{x} (r_{0}) (x - x_{0}) + f_{y} (r_{0}) (y - y_{0}) + f_{z} (r_{0}) (z - z_{0}) = 0$ で与えられます。コンパクトな数学的表記では、接平面の方程式を $\nabla f (r_{0}) \cdot (r - r_{0}) = 0$ のように記述できます。

関数gradientを使用して、 $f (r)$ の勾配を求めます。結果が 3 行 1 列のシンボリック行列変数となることに注意してください。

fgrad = gradient(f,r)

fgrad =  $2 r^{T}$

size(fgrad)

ans = 1×2

     3     1

接平面の方程式を定義します。関数subsを使用して、点 $r_{0} = ⟨ 1, - 2, 3 ⟩$ における勾配を評価します。

r0 = [-2,1,3];
fplane = (r-r0)*subs(fgrad,r,r0)

fplane = 
 $\begin{array}{l} 2 (- Σ_{1} + r) {Σ_{1}}^{T} \\ where \\ Σ_{1} = (\begin{array}{c} - 2 & 1 & 3 \end{array}) \end{array}$

plot3を使用して点 $r_{0}$ をプロットし、fimplicit3 を使用して接平面をプロットします。

hold on
plot3(r0(1),r0(2),r0(3),'ro',MarkerSize = 10,MarkerFaceColor = 'r')
fimplicit3(symmatrix2sym(fplane == 0))

点 $r_{0}$ における法線の方程式は、 $n (t) = ⟨ x_{0}, y_{0}, z_{0} ⟩ + t ⟨ f_{x} (r_{0}), f_{y} (r_{0}), f_{z} (r_{0}) ⟩$ で与えられます。コンパクトな数学的表記では、この方程式を $n (t) = r_{0} + t \nabla f (r_{0})$ のように記述できます。

法線の方程式を定義します。

syms t
n = r0 + t*subs(fgrad,r,r0).'

n = 
 $\begin{array}{l} Σ_{1} + 2 t Σ_{1} \\ where \\ Σ_{1} = (\begin{array}{c} - 2 & 1 & 3 \end{array}) \end{array}$

symmatrix2sym を使用して、法線の方程式を syms データ型に変換します。n にインデックスを付けて、法線のパラメトリック曲線 $x (t)$ 、 $y (t)$ 、および $z (t)$ を抽出します。fplot3を使用して法線をプロットします。

n = symmatrix2sym(n)

n =  $(\begin{array}{c} - 4 t - 2 & 2 t + 1 & 6 t + 3 \end{array})$

fplot3(n(1),n(2),n(3),[0 1],'r->')