cell2sym
cell 配列をシンボリック配列に変換
説明
S = cell2sym(C)C をシンボリック配列 S に変換します。C の要素はシンボリック オブジェクトに変換可能でなければなりません。
入力 cell 配列 C の各要素がスカラーの場合、size(S) = size(C) であり、すべてのインデックス k について S(k) = sym(C(k)) となります。cell 配列 C に非スカラー要素が含まれる場合、C の内容は N 次元の四角形への連結に対応していなければなりません。それ以外の場合、結果は定義されません。たとえば、同じ列の cell の内容は、同じ列数でなければなりません。ただし、行数は必ずしも同じにする必要はありません。図を参照してください。
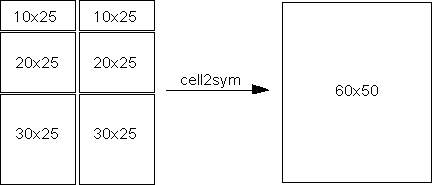
例
入力引数
出力引数
バージョン履歴
R2016a で導入