このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

airy

エアリー関数

構文

airy(x)

airy(0,x)

airy(1,x)

airy(2,x)

airy(3,x)

airy(n,x)

airy(___,1)

説明

airy(x) は、第 1 種 エアリー関数 Ai(x) を、x の各要素について返します。

airy(0,x) は、airy(x) と同じ結果になります。

airy(1,x) は、Ai(x) の導関数を返します。

airy(2,x) は、第 2 種エアリー関数 Bi(x) を返します。

airy(3,x) は、Bi(x) の導関数を返します。

airy(n,x) は、ベクトル n の値を使用して、ベクトル x の要素の対応するエアリー関数を返します。n と x は同じサイズでなければなりません。

airy(___,1) は、MATLAB^® の関数 airy の構文に従ってスケーリングされたエアリー関数を返します。

例

第 1 種エアリー関数を求める

airy を使用して、数値入力またはシンボリック入力に対する第 1 種エアリー関数 Ai(x) を求めます。vpa を使用して、シンボリック厳密解の出力を近似します。

1.5 における第 1 種エアリー関数 Ai(x) を求めます。入力は double でシンボリックではないため、結果は double になります。

airy(1.5)

ans =
    0.0717

sym を使用してベクトル v をシンボリック型に変換し、v の値のエアリー関数をシンボリックに求めます。入力はシンボリックであるため、airy はシンボリック厳密解の結果を返します。ほとんどのシンボリックな入力に対するシンボリック厳密解の結果は、未解決の関数呼び出しになります。

v = sym([-1 0 25.1 1+1i]);
vAiry = airy(v)

vAiry =
[ airy(0, -1), 3^(1/3)/(3*gamma(2/3)), airy(0, 251/10), airy(0, 1 + 1i)]

vpa を使用して、シンボリック厳密解の結果を数値的に近似します。

vpa(vAiry)

ans =
[ 0.53556088329235211879951656563887, 0.35502805388781723926006318600418,...
 4.9152763177499054787371976959487e-38,...
 0.060458308371838149196532978116646 - 0.15188956587718140235494791259223i]

シンボリック入力 x^2 のエアリー関数 Ai(x) を求めます。シンボリック式に対して、airy では未解決の呼び出しが返されます。

syms x
airy(x^2)

ans =
airy(0, x^2)

第 2 種エアリー関数を求める

最初の引数に 2 を指定して、シンボリック入力 [-3 4 1+1i x^2] の第 2 種エアリー関数 Bi(x) を求めます。入力はシンボリックであるため、airy はシンボリック厳密解の結果を返します。ほとんどのシンボリックな入力に対するシンボリック厳密解の結果は、未解決の関数呼び出しになります。

v = sym([-3 4 1+1i x^2]);
vAiry = airy(2, v)

vAiry =
[ airy(2, -3), airy(2, 4), airy(2, 1 + 1i), airy(2, x^2)]

第 1 種エアリー関数を求めるの例で説明されているように、airy(x) に類似した構文 airy(2,x) を使用します。

エアリー関数のプロット

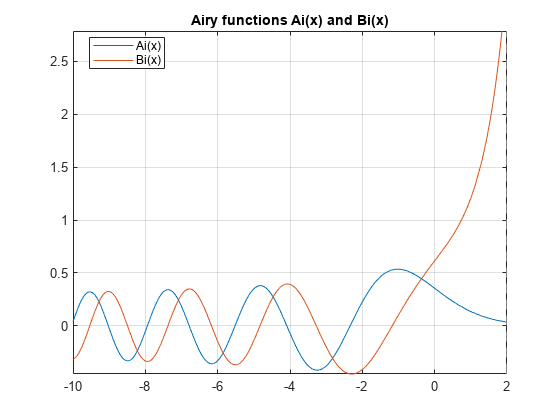
fplot を使用して、エアリー関数 $$Ai(x)$$ と $$Bi(x)$$ を [-10 2] の区間でプロットします。

syms x
fplot(airy(x), [-10 2])
hold on
fplot(airy(2,x), [-10 2])
legend('Ai(x)','Bi(x)','Location','Best')
title('Airy functions Ai(x) and Bi(x)')
grid on
hold off

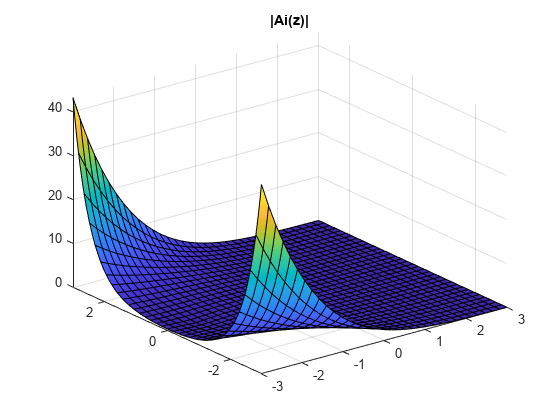
複素平面上に $$Ai(z)$$ の絶対値をプロットします。

syms y
z = x + 1i*y;
fsurf(abs(airy(z)),[-3 3 -3 3])
title('|Ai(z)|')

エアリー関数の導関数を求める

airy の最初の引数に 1 を指定して、0 における第 1 種エアリー関数の導関数 Ai′(x) を求めます。次に、vpa を使用して、導関数を数値的に近似します。

dAi = airy(1, sym(0))
dAi_vpa = vpa(dAi)

dAi =
-(3^(1/6)*gamma(2/3))/(2*pi)
dAi_vpa =
-0.2588194037928067984051835601892

最初の引数に 3 を指定して、x における第 2 種エアリー関数の導関数 Bi′(x) を求めます。次に、subs を使用して x への代入を行い、vpa を呼び出して、x = 5 における導関数を求めます。

syms x
dBi = airy(3, x)
dBi_vpa = vpa(subs(dBi, x, 5))

dBi =
airy(3, x)
dBi_vpa =
1435.8190802179825186717212380046

エアリー関数のエアリー微分方程式の求解

エアリー関数 Ai(x) および Bi(x) が微分方程式

$$\frac{{\partial }^{2}y}{\partial x^2}-xy=0.$$

の解であることを示します。

syms y(x)
dsolve(diff(y, 2) - x*y == 0)

ans =
C1*airy(0, x) + C2*airy(2, x)

エアリー関数の微分

airy を含む式を微分します。

syms x y
diff(airy(x^2))
diff(diff(airy(3, x^2 + x*y -y^2), x), y)

ans =
2*x*airy(1, x^2)
 
ans =
airy(2, x^2 + x*y - y^2)*(x^2 + x*y - y^2) +...
airy(2, x^2 + x*y - y^2)*(x - 2*y)*(2*x + y) +...
airy(3, x^2 + x*y - y^2)*(x - 2*y)*(2*x + y)*(x^2 + x*y - y^2)
 

テイラー級数を使用したエアリー関数の展開

taylor を使用して、エアリー関数 Ai(x) および Bi(x) のテイラー級数展開を求めます。

aiTaylor = taylor(airy(x))
biTaylor = taylor(airy(2, x))

aiTaylor =
- (3^(1/6)*gamma(2/3)*x^4)/(24*pi) + (3^(1/3)*x^3)/(18*gamma(2/3))...
 - (3^(1/6)*gamma(2/3)*x)/(2*pi) + 3^(1/3)/(3*gamma(2/3))
biTaylor =
(3^(2/3)*gamma(2/3)*x^4)/(24*pi) + (3^(5/6)*x^3)/(18*gamma(2/3))...
 + (3^(2/3)*gamma(2/3)*x)/(2*pi) + 3^(5/6)/(3*gamma(2/3))

エアリー関数のフーリエ変換

fourier を使用して、エアリー関数 Ai(x) のフーリエ変換を求めます。

syms x
aiFourier = fourier(airy(x))

aiFourier =
exp((w^3*1i)/3)

エアリー関数の数値根

vpasolve を使用して、エアリー関数 Ai(x) の根を数値的に求めます。

syms x
vpasolve(airy(x) == 0, x)

ans =
 -226.99630507523600716771890962744

区間 [-5 -3] における根を求めます。

vpasolve(airy(x) == 0, x, [-5 -3])

ans =
-4.0879494441309706166369887014574

入力引数

x — 入力

数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック変数 | シンボリック ベクトル | シンボリック行列 | シンボリック多次元配列 | シンボリック関数 | シンボリック式

入力。数値、ベクトル、行列または多次元配列、あるいはシンボリック数、変数、ベクトル、行列、多次元配列、関数または式として指定します。

n — エアリー関数の種類

0 (既定値) | 数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック変数 | シンボリック ベクトル | シンボリック行列 | シンボリック多次元配列

エアリー関数の種類。数値、ベクトル、行列または多次元配列、あるいはシンボリック数、変数、ベクトル、行列または多次元配列として指定します。入力値は 0、1、2 または 3 でなければなりません。これらの入力値はエアリー関数を以下のように指定します。

n	戻り値
0 (既定値)	エアリー関数 Ai(x)。これは airy(x) と同じです。
1	エアリー関数の導関数 Ai’(x)。
2	第 2 種のエアリー関数 Bi(x)。
3	第 2 種のエアリー関数の導関数 Bi’(x)。

詳細

エアリー関数

エアリー関数 Ai(x) および Bi(x) は、次の微分方程式の 2 つの線形独立解です。

$$\frac{{\partial }^{2}y}{\partial x^2}-xy=0.$$

Ai(x) は第 1 種エアリー関数と呼ばれます。Bi(x) は第 2 種エアリー関数と呼ばれます。

スケーリングされたエアリー関数

第 1 種エアリー関数 Ai(x) は、次のようにスケーリングされます。

$$e^{\left(\frac{2}{3}{x}^{\left(3/2\right)}\right)}\text{Ai}\left(x\right).$$

導関数 Ai’(x) は、同じ係数でスケーリングされます。

第 2 種エアリー関数 Bi(x) は、次のようにスケーリングされます。

$$e^{-\left|\frac{2}{3}\text{Re}\left(x^{\left(3/2\right)}\right)\right|}\text{Bi}\left(x\right).$$

導関数 Bi’(x) は、同じ係数でスケーリングされます。

ヒント

• シンボリック オブジェクトではない入力について airy を呼び出すと、MATLAB の関数 airy が呼び出されます。

• airy(n, x) を呼び出す際、少なくとも一方の引数がスカラーであるか、または両方の引数が同じサイズのベクトルまたは行列でなければなりません。一方の引数がスカラーであり、もう一方の引数がベクトルまたは行列である場合、スカラーは airy(n,x) によってすべての要素がそのスカラーと等しい、もう一方の引数と同じサイズのベクトルまたは行列に拡張されます。

• airy は、0 における特別な厳密値を返します。

バージョン履歴

R2012a で導入

参考

besseli | besselj | besselk | bessely