slicesample
スライス サンプラー
構文
説明
rnd = slicesample(___,Name,Value)
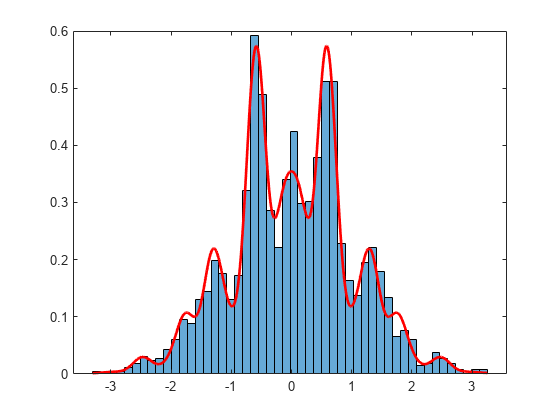
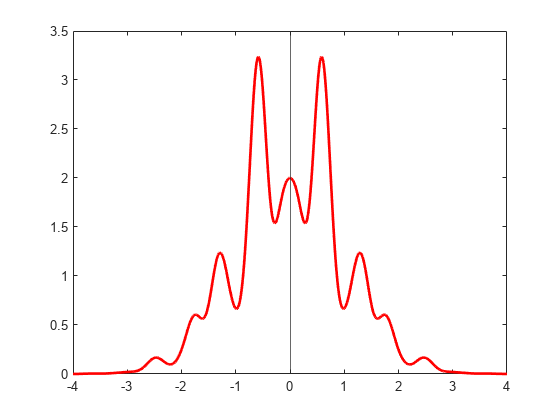
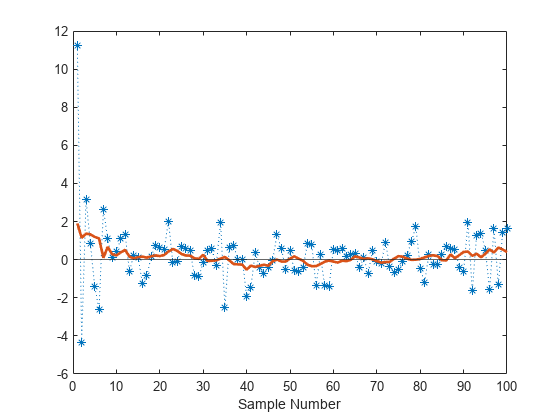
例
入力引数
名前と値の引数
出力引数
ヒント
数値的なオーバーフローやアンダーフローのエラーが発生する可能性がある密度関数には、
pdfの代わりにlogpdfを使用します。thinとburninの適切な値を判断するための明確なガイドラインはありません。thinとburninの開始値を指定した後、標本の独立性と類似性がターゲットの密度関数に応じた必要な状態になるまで、必要に応じてそれらを増やしていきます。標本の生成時に関数評価の回数が最大数の 200 を超えてステップアウト手順 (アルゴリズムを参照) が失敗する場合は、必要に応じて
widthを別の値にして試してみます。widthが小さすぎると、スライスの範囲を特定するためにアルゴリズムで過剰な数の関数評価が実装される可能性があります。widthが大きすぎると、幅を適切なサイズに縮小するようにアルゴリズムで試行され、結果として関数評価の数が多くなることがあります。標本ごとの関数評価の平均回数は出力引数nevalで返されます。
アルゴリズム
スライス サンプリングは、比例定数までしかわかっていないときに、任意の密度関数を使用して分布から標本を抽出するマルコフ連鎖モンテカルロ (MCMC) アルゴリズムです。このような状況としては、正規化定数が未知である複雑なベイズ事後分布からサンプリングしなければならない場合などがあります。このアルゴリズムでは、独立した標本は生成されず、定常分布が対象の分布であるマルコフ連鎖が生成されます。
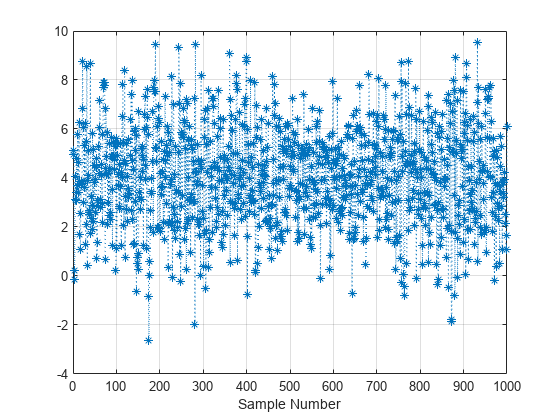
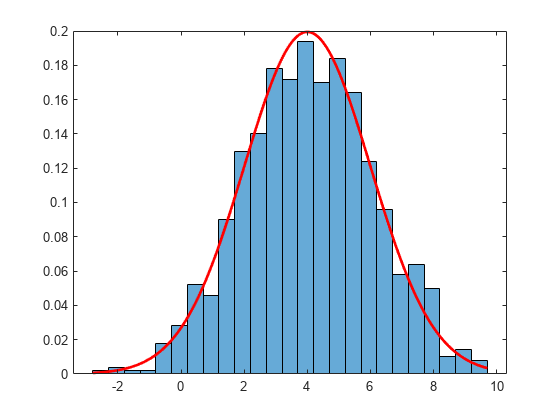
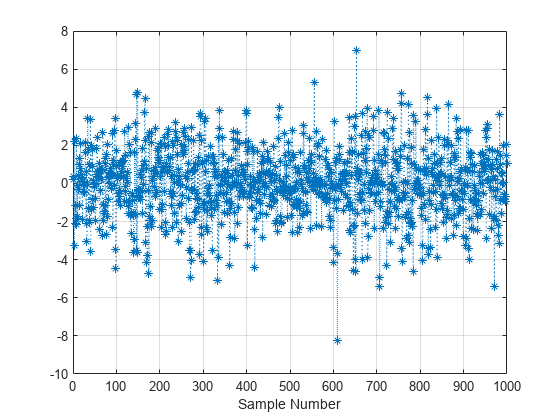
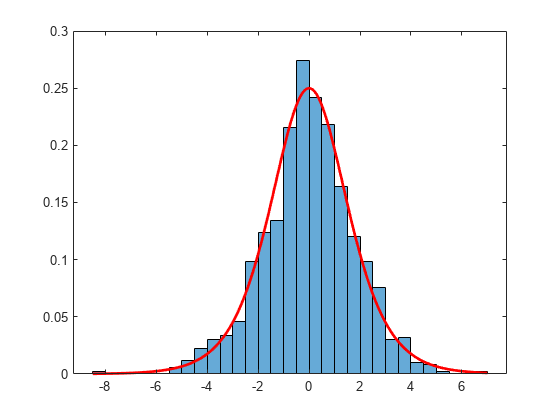
関数 slicesample は、垂直方向と水平方向のステップの列を使って、密度関数の下の領域から標本を抽出します。はじめに、0 から指定された初期値 x の密度関数 f(x) の値までの間で、無作為に高さを選択します。次に、選択された高さよりも密度関数が大きくなるすべての x の値を含む水平方向の "スライス" からサンプリングすることによって、新しい x の値を無作為に選択します。関数 slicesample は、多変量分布の場合にも同様のスライス サンプリング アルゴリズムを使用します。
ターゲットの密度関数に比例する密度関数 f(x) を選択し、以下を実行して乱数のマルコフ連鎖を生成します。
f(x) の定義域内にある初期値 x(t) を選択します。
(0, f(x(t))) から実数 y を等間隔に抽出することで、水平方向の "スライス" を S = {x: y < f(x)} として定義します。
すべてまたはほとんどの "スライス" S を含む x(t) 周辺の区間 I = (L, R) を検出します。
この区間内から新たな点 x(t + 1) を抽出します。
t を 1 ずつインクリメントし、目的とする標本数が得られるまで手順 2 から 4 を繰り返します。
slicesample では、Neal のスライス サンプリング アルゴリズム ([1]) を使用しています。数値安定性のために、slicesample は関数 pdf の対数に対して演算を行います (引数 logpdf が指定されている場合は除く)。slicesample は、スライス S を含む区間 I を見つけるために Neal の "ステップアウト" と "ステップイン" の手法を使用します。各標本の生成時にステップアウトとステップインの反復がそれぞれ最大 200 回まで試行されます。
連鎖内の近接点は、独立した値の標本からよりも互いに接近した値になる傾向があります。多くの目的で、点のセット全体を対象の分布からの標本として使用できます。ただし、この種の系列相関が問題となる場合は、名前と値の引数 burnin および thin を使用して相関を減らすことができます。
代替機能
slicesampleは、特に中次元と高次元の密度関数について、混合が遅く定常分布に収束するまで時間がかかるマルコフ連鎖を生成する可能性があります。このような場合にサンプリングを高速化するには、勾配に基づくハミルトニアン モンテカルロ (HMC) サンプラーhmcSamplerを使用します。マルコフ連鎖サンプラーを使用する標本分布の表現を参照してください。
参照
[1] Neal, Radford M. "Slice Sampling." The Annals of Statistics Vol. 31, No. 3, pp. 705–767, 2003. Available at https://doi.org/10.1214/aos/1056562461.
バージョン履歴
R2006a で導入