機械学習を使用したバッテリーの SOC の予測

この例では次を使用します。

この例では、ガウス過程回帰 (GPR) モデルに学習させて、自動車エンジニアリングでバッテリーの SOC を予測する方法を示します。

バッテリーの充電状態 (SOC) は、電気バッテリーの充電レベルを容量に対する割合として測定したものです。SOC は車両のエネルギーマネジメントシステムに不可欠な情報で、信頼性に優れた手頃な電動車 (xEV) を実現するには、SOC を正確に推定する必要があります。しかし、リチウムイオンバッテリーの温度、健全性、および SOC 依存動作は非線形であるため、SOC の推定は自動車エンジニアリングの大きな課題となっています。この問題に対する従来の電気化学モデルなどのアプローチでは、通常、バッテリーの組成や物理的応答についての正確なパラメーターと知識が必要になります。一方、機械学習モデルの使用は、データ駆動型のアプローチであり、バッテリーやその非線形動作についての必要な知識が最小限で済みます [1]。

この例では、電圧、電流、温度、平均電圧と平均電流 (過去 500 秒間) などのバッテリーのさまざまな特徴量を表す時系列データに基づいて、ガウス過程回帰モデルに学習させて、車両のリチウムイオンバッテリーの SOC を予測します。

回帰モデルに学習をさせた後、そのモデルを使用して Simulink® モデルを作成し、その Simulink モデルから展開用に HDL コードを生成できます。詳細については、ニューラルネットワーク回帰モデルの FPGA/ASIC プラットフォームへの展開を参照してください。

データの読み込み

[1] の前処理済みデータセット LG_HG2_Prepared_Dataset_McMasterUniversity_Jan_2020 のサブセットである batterySOC データセットを読み込みます。オプションのセクションであるデータのダウンロードと準備では、データセットをダウンロードし、サブセットを作成して batterySOC.mat ファイルに格納するための準備を行う方法を示しています。

load("batterySOC.mat")

データセットには、1 つの学習データの table (trainData) と 4 つのテストデータの table (testDataN10deg、testData0deg、testData10deg および testData25deg) があります。学習データは、4 つの異なる周囲温度 (摂氏 –10 度、0 度、10 度、25 度) における走行サイクル中にバッテリーが電気自動車に電力供給していた際に収集された実験データの単一のシーケンスです。テストデータは実験データの 4 つのシーケンスで構成され、各シーケンスは前述と同じ 4 つの温度のいずれかで収集されています。テストデータセットが格納されている cell 配列を作成します。

testData = cell(4,1);
testData{1} = testDataN10deg;
testData{2} = testData0deg;
testData{3} = testData10deg;
testData{4} = testData25deg;
testDataName = ["-10^{\circ}C","0^{\circ}C", ...
    "10^{\circ}C","25^{\circ}C"];

学習とテストの各 table は、前処理済みデータ LG_HG2_Prepared_Dataset_McMasterUniversity_Jan_2020 のサブセットで、100 秒ごとにデータ点が設定されるようにサンプリングされています。学習データセットの最初の数行をプレビューします。

head(trainData)

    Voltage    Current    Temperature    AverageVoltage    AverageCurrent      SOC  
    _______    _______    ___________    ______________    ______________    _______

    0.38515    0.75102       0.3031         0.38515           0.75102        0.20642
    0.38546    0.75102      0.45607          0.3853           0.75102        0.20642
     0.3855    0.75102      0.62209         0.38537           0.75102        0.20642
    0.38565    0.75102      0.77026         0.38544           0.75102        0.20642
    0.38643    0.75102      0.84667         0.38564           0.75102        0.20642
    0.38778    0.75102      0.85707         0.38599           0.75102        0.20642
    0.38915    0.75102      0.85474         0.38666           0.75102        0.20642
    0.39024    0.75102      0.87646         0.38746           0.75102        0.20642

学習とテストの各 table には、Voltage、Current、Temperature、AverageVoltage、AverageTemperature および SOC の 6 つの変数が含まれています。学習データとテストデータの変数値をプロットします。プロットする変数を選択します。

variableToPlot = "SOC";
figure
t = tiledlayout(3,2);
nexttile(1,[1,2])
trainDataT = (0:(size(trainData,1)-1))'*100;
plot(trainDataT,trainData.(variableToPlot))
title("Training Data")
for i = 1 : 4
    nexttile
    currentTestData = testData{i};
    currentTestDataT = (0:(size(currentTestData,1)-1))'*100;
    plot(currentTestDataT,currentTestData.(variableToPlot))
    title(join(["Test Data at",testDataName(i)]))
end
linkaxes(t.Children,"y")
xlabel(t,"Time (seconds)")
ylabel(t,variableToPlot)

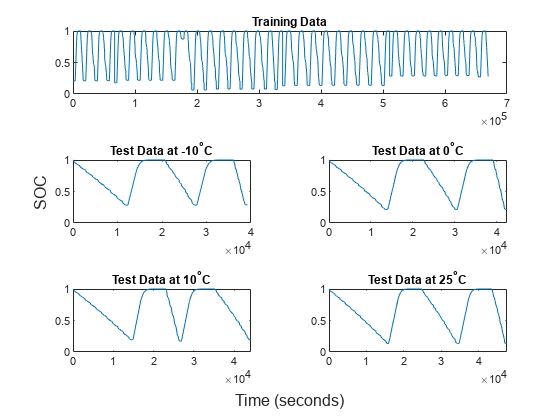
6 つの変数はすべて [0,1] の範囲内にあります。満充電のバッテリーの SOC 値は 1 で、完全に放電済みのバッテリーの SOC 値は 0 です。したがって、SOC 値は [0,1] の範囲になければなりません。

ガウス過程回帰モデルの学習

関数 fitrgp を使用して GPR モデルに学習させます。名前と値の引数 OptimizeHyperparameters を ["BasisFunction","KernelFunction","Standardize"] として指定します。この関数は、指定されたハイパーパラメーターに最適な値を求めてから、モデルを当てはめます。再現性を得るために、乱数シードを設定し、expected-improvement-plus の獲得関数を使用します。また、ベイズ最適化を並列実行するよう UseParallel=true を指定します。並列計算には Parallel Computing Toolbox™ が必要です。

rng("default")
Mdl = fitrgp(trainData,"SOC", ...
    OptimizeHyperparameters=["BasisFunction","KernelFunction","Standardize"], ...
    HyperparameterOptimizationOptions= ...
    struct(AcquisitionFunctionName="expected-improvement-plus",UseParallel=true))

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to the parallel pool (number of workers: 6).
Copying objective function to workers...
Done copying objective function to workers.
|==============================================================================================================================|
| Iter | Active  | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   | BasisFunction| KernelFuncti-|  Standardize |
|      | workers | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              | on           |              |
|==============================================================================================================================|
|    1 |       6 | Best   |  0.00051935 |      98.995 |  0.00051935 |  0.00051935 |     constant |     matern52 |        false |
|    2 |       6 | Accept |  0.00054243 |      112.15 |  0.00051935 |  0.00052044 | pureQuadrati |     matern52 |        false |
|    3 |       6 | Accept |  0.00052242 |      98.911 |  0.00051935 |  0.00052111 |     constant |     matern52 |        false |
|    4 |       6 | Accept |  0.00052343 |      127.13 |  0.00051935 |   0.0005211 | pureQuadrati |  exponential |         true |
|    5 |       6 | Accept |  0.00058425 |      249.88 |  0.00051935 |  0.00052097 |         none | rationalquad |         true |
|    6 |       6 | Best   |  0.00050934 |      105.61 |  0.00050934 |  0.00050952 |     constant |     matern32 |        false |
|    7 |       6 | Accept |  0.00052931 |      339.37 |  0.00050934 |  0.00050954 |     constant |  ardmatern32 |         true |
|    8 |       6 | Accept |  0.00053765 |      94.526 |  0.00050934 |  0.00050958 |         none |     matern52 |        false |
|    9 |       6 | Accept |  0.00061936 |      355.38 |  0.00050934 |  0.00050948 |     constant | ardsquaredex |         true |
|   10 |       6 | Accept |  0.00057228 |      382.03 |  0.00050934 |   0.0005095 |         none |  ardmatern32 |        false |
|   11 |       6 | Accept |  0.00053971 |      99.533 |  0.00050934 |  0.00050951 |     constant |     matern32 |         true |
|   12 |       6 | Accept |  0.00051496 |      91.813 |  0.00050934 |   0.0005095 |         none |     matern32 |        false |
|   13 |       6 | Accept |  0.00057599 |      97.529 |  0.00050934 |  0.00050951 |     constant |     matern52 |         true |
|   14 |       6 | Best   |  0.00040178 |      109.22 |  0.00040178 |  0.00040204 |     constant |  exponential |        false |
|   15 |       6 | Accept |  0.00051895 |      226.34 |  0.00040178 |  0.00040206 |     constant | rationalquad |        false |
|   16 |       6 | Accept |  0.00054575 |      105.36 |  0.00040178 |  0.00040208 | pureQuadrati |     matern32 |         true |
|   17 |       6 | Accept |  0.00053792 |      88.646 |  0.00040178 |   0.0004021 |         none |     matern32 |         true |
|   18 |       6 | Accept |  0.00041535 |      115.14 |  0.00040178 |    0.000402 | pureQuadrati |  exponential |        false |
|   19 |       6 | Best   |  0.00039856 |      94.383 |  0.00039856 |  0.00039873 |         none |  exponential |        false |
|   20 |       6 | Accept |  0.00040507 |      106.15 |  0.00039856 |  0.00039874 |     constant |  exponential |        false |
|==============================================================================================================================|
| Iter | Active  | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   | BasisFunction| KernelFuncti-|  Standardize |
|      | workers | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              | on           |              |
|==============================================================================================================================|
|   21 |       6 | Accept |  0.00040581 |      102.97 |  0.00039856 |  0.00039873 |     constant |  exponential |        false |
|   22 |       6 | Accept |  0.00040278 |      108.56 |  0.00039856 |   0.0003987 |     constant |  exponential |        false |
|   23 |       6 | Accept |  0.00040521 |      93.324 |  0.00039856 |  0.00040202 |         none |  exponential |        false |
|   24 |       6 | Accept |  0.00040458 |      88.379 |  0.00039856 |  0.00040287 |         none |  exponential |        false |
|   25 |       6 | Accept |  0.00040195 |      88.728 |  0.00039856 |  0.00040263 |         none |  exponential |        false |
|   26 |       6 | Accept |  0.00041476 |      99.863 |  0.00039856 |  0.00040262 |       linear |  exponential |        false |
|   27 |       6 | Accept |  0.00042907 |      96.641 |  0.00039856 |  0.00040262 |         none |  exponential |         true |
|   28 |       6 | Accept |  0.00052144 |      100.62 |  0.00039856 |  0.00040262 | pureQuadrati |     matern32 |        false |
|   29 |       6 | Accept |  0.00062455 |      293.96 |  0.00039856 |  0.00040262 |     constant | ardsquaredex |        false |
|   30 |       6 | Accept |  0.00044598 |       98.27 |  0.00039856 |  0.00040262 |       linear |  exponential |         true |

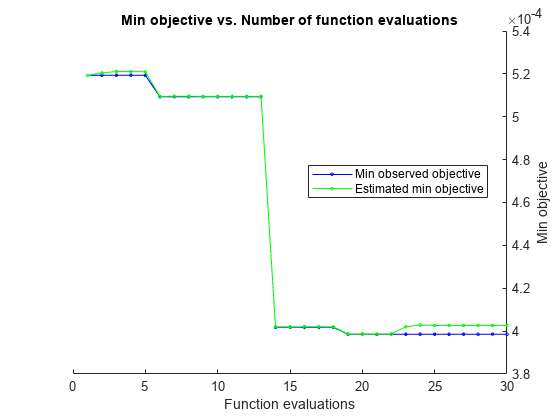
Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 848.1224 seconds
Total objective function evaluation time: 4269.4267

Best observed feasible point:
    BasisFunction    KernelFunction    Standardize
    _____________    ______________    ___________

        none          exponential         false   

Observed objective function value = 0.00039856
Estimated objective function value = 0.00040262
Function evaluation time = 94.3834

Best estimated feasible point (according to models):
    BasisFunction    KernelFunction    Standardize
    _____________    ______________    ___________

        none          exponential         false   

Estimated objective function value = 0.00040262
Estimated function evaluation time = 91.1934

Mdl = 
  RegressionGP
                       PredictorNames: {'Voltage'  'Current'  'Temperature'  'AverageVoltage'  'AverageCurrent'}
                         ResponseName: 'SOC'
                CategoricalPredictors: []
                    ResponseTransform: 'none'
                      NumObservations: 6702
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]
                       KernelFunction: 'Exponential'
                    KernelInformation: [1×1 struct]
                        BasisFunction: 'None'
                                 Beta: [0×1 double]
                                Sigma: 0.0176
                    PredictorLocation: []
                       PredictorScale: []
                                Alpha: [6702×1 double]
                     ActiveSetVectors: [6702×5 double]
                        PredictMethod: 'Exact'
                        ActiveSetSize: 2000
                            FitMethod: 'SD'
                      ActiveSetMethod: 'Random'
                    IsActiveSetVector: [6702×1 logical]
                        LogLikelihood: 4.5248e+03
                     ActiveSetHistory: [1×1 struct]
                       BCDInformation: []


  Properties, Methods

Mdl は RegressionGP モデルオブジェクトです。RegressionGP の関数 predict および loss を使用して、予測 SOC 値と平均二乗誤差 (MSE) をそれぞれ計算できます。バッテリーの SOC 値は [0,1] の範囲になければならないことを思い出してください。ただし、GPR モデルの関数 predict は、この範囲からわずかに外れる値を返す可能性があります。値がこの範囲に確実に留まるようにするには、予測値に関数 min および max を適用します。また、GPR モデルの関数 loss は、関数 predict によって返された予測を使用して平均二乗誤差 (MSE) を計算します。代わりに、[0,1] の範囲にトリミングされた予測値を使用して誤差を計算するカスタム損失関数を定義できます。

ResponseTransform をサポートする別のタイプの回帰モデルを使用する場合は、モデルの ResponseTransform プロパティを @(y) min(max(y,0),1) として指定して、関数 predict および loss を使用できます。RegressionGP では ResponseTransform はサポートされていません。

または、ロジット変換を使用して SOC 値を無制限の範囲に変換できます。その後、変換したデータを使用して回帰モデルに学習させ、逆ロジット変換を使用して予測値を制限された範囲に戻すことができます。

回帰モデルのテスト

学習データセットとテストデータセットの予測 SOC 値と実際の SOC 値をプロットします。関数 min および max を使用して、予測値を [0,1] の範囲内に維持します。

figure
t = tiledlayout(3,2);
nexttile(1,[1,2])
plot(trainDataT,trainData.SOC)
hold on
plot(trainDataT,min(max(resubPredict(Mdl),0),1))
hold off
ylim([0,1])
legend(["True SOC","Predicted SOC"], ...
    Location="northoutside",Orientation="horizontal")
title("Training Data")

predictedSOC = cell(4,1);
for i = 1 : 4
    nexttile
    currentTestData = testData{i};
    currentTestDataT = (0:(size(currentTestData,1)-1))'*100;
    predictedSOC{i} = min(max(predict(Mdl,currentTestData),0),1);
    plot(currentTestDataT,currentTestData.SOC)
    hold on
    plot(currentTestDataT,predictedSOC{i})
    hold off
    ylim([0,1])
    title(join(["Test Data at",testDataName(i)]))
end

xlabel(t,"Time (seconds)")
ylabel(t,"Battery SOC")

各周囲温度について予測 SOC とターゲット SOC の間の平方根平均二乗誤差 (RMSE) と最大絶対誤差を計算します。トリミングされた予測値に基づいて損失値を計算するカスタム損失関数を指定します。

testRMSE = NaN(4,1);
testMaxAbsError = NaN(4,1);
lossFun_RMSE = @(y,ypred,w) sqrt(mean((y-min(max(ypred,0),1)).^2));
lossFun_MaxAbsError = @(y,ypred,w) max(abs(y-min(max(ypred,0),1)));
for i = 1: 4
    testRMSE(i) = loss(Mdl,testData{i},LossFun=lossFun_RMSE);
    testMaxAbsError(i) = loss(Mdl,testData{i},LossFun=lossFun_MaxAbsError);
end

RMSE と最大絶対誤差の値をプロットします。

figure
tiledlayout(2,1)
nexttile
bar(testRMSE)
xticklabels(testDataName)
xlabel("Ambient Temperature")
ylabel("RMSE")
nexttile
bar(testMaxAbsError)
xticklabels(testDataName)
xlabel("Ambient Temperature")
ylabel("Maximum Absolute Error")

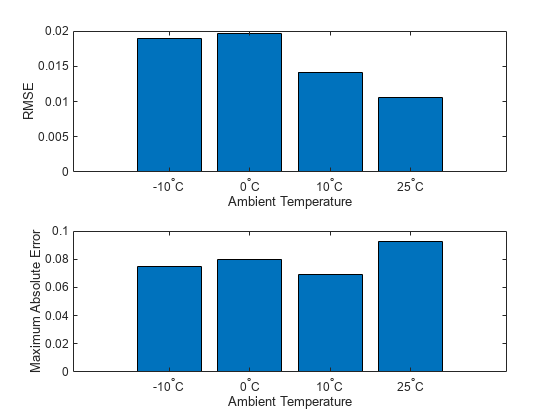
Figure contains 2 axes objects. Axes object 1 contains an object of type bar. Axes object 2 contains an object of type bar.

RMSE と最大絶対誤差のプロットの値が小さいほど、対応する温度の予測の精度が高いことを示します。同じプロットの値が大きいほど、対応する温度の予測の精度が低いことを示します。

データのダウンロードと準備 (オプション)

前述のように、この例では、[1] の前処理済みデータセット LG_HG2_Prepared_Dataset_McMasterUniversity_Jan_2020 のサブセットを使用します。このサブセットを提供されているファイル batterySOC.mat から読み込むか、このセクションで説明されているようにデータセットをダウンロードして前処理できます。

データセット LG_HG2_Prepared_Dataset_McMasterUniversity_Jan_2020 の各ファイルには、5 つの予測子 (電圧、電流、温度、平均電圧、および平均電流) の時系列 X と 1 つのターゲット (SOC) の時系列 Y が含まれています。各ファイルは、異なる周囲温度で収集されたデータを表します。

データセットをダウンロードする URL を指定します。または、このデータセットを https://data.mendeley.com/datasets/cp3473x7xv/3 から手動でダウンロードできます。

url = "https://data.mendeley.com/public-files/datasets/cp3473x7xv/files/ad7ac5c9-2b9e-458a-a91f-6f3da449bdfb/file_downloaded";

downloadFolder を ZIP ファイルのダウンロード先に設定し、outputFolder を ZIP ファイルの解凍先に設定します。

downloadFolder = tempdir;
outputFolder = fullfile(downloadFolder,"LGHG2@n10C_to_25degC");

データセット LG_HG2_Prepared_Dataset_McMasterUniversity_Jan_2020 をダウンロードして解凍します。

if ~exist(outputFolder,"dir")
    fprintf("Downloading LGHG2@n10C_to_25degC.zip (56 MB) ... ")
    filename = fullfile(downloadFolder,"LGHG2@n10C_to_25degC.zip");
    websave(filename,url);
    unzip(filename,outputFolder)
end

学習データとテストデータの両方のファイルデータストアを作成し、読み取り関数を関数 load として指定します。関数 load は、データを MAT ファイルからデータストアに読み込みます。

folderTrain = fullfile(outputFolder,"Train");
folderTest = fullfile(outputFolder,"Test");
fdsTrain = fileDatastore(folderTrain,ReadFcn=@load);
fdsTest = fileDatastore(folderTest,ReadFcn=@load);

データストア内のすべてのデータを読み取ります。

trainDataFull = read(fdsTrain);
testDataFull = readall(fdsTest);
testDataFullN10deg = testDataFull{1};
testDataFull0deg   = testDataFull{2};
testDataFull10deg  = testDataFull{3};
testDataFull25deg  = testDataFull{4};

100 秒ごとに 1 つのデータ点が設定されるようにデータセットをリサンプリングし、補助関数 helperMovingAverage を使用して移動平均を計算します。この関数のコードは、この例の終わりで示します。

idx0 = 1:184257;
idx10 = 184258:337973;
idx25 = 337974:510530;
idxN10 = 510531:669956;
trainData0deg   = helperMovingAverage(array2table([trainDataFull.X(:,idx0);   trainDataFull.Y(idx0)]'));
trainData10deg  = helperMovingAverage(array2table([trainDataFull.X(:,idx10);  trainDataFull.Y(idx10)]'));
trainData25deg  = helperMovingAverage(array2table([trainDataFull.X(:,idx25);  trainDataFull.Y(idx25)]'));
trainDataN10deg = helperMovingAverage(array2table([trainDataFull.X(:,idxN10); trainDataFull.Y(idxN10)]'));
trainData = [trainData0deg; trainData10deg; trainData25deg; trainDataN10deg];

testDataN10deg = helperMovingAverage(array2table([testDataFullN10deg.X; testDataFullN10deg.Y]'));
testData0deg   = helperMovingAverage(array2table([testDataFull0deg.X;   testDataFull0deg.Y]'));
testData10deg  = helperMovingAverage(array2table([testDataFull10deg.X;  testDataFull10deg.Y]'));
testData25deg  = helperMovingAverage(array2table([testDataFull25deg.X;  testDataFull25deg.Y]'));

batterySOC.mat ファイルには、変数 trainData、testDataN10deg、testData0deg、testData10deg、testData25deg が含まれています。

補助関数

次のコードは、補助関数 helperMovingAverage を作成します。

function newTbl = helperMovingAverage(tbl)

newTbl = tbl(1:100:end,[1:3,end]);
variableNames = ["Voltage","Current","Temperature","SOC"];
newTbl.Properties.VariableNames = variableNames;

n = size(newTbl,1);
newTbl.AverageVoltage = NaN(n,1);
newTbl.AverageCurrent = NaN(n,1);

for i = 1 : n
    newTbl.AverageVoltage(i) = mean(newTbl.Voltage(max(1,i-5):i));
    newTbl.AverageCurrent(i) = mean(newTbl.Current(max(1,i-5):i));
end

newTbl = movevars(newTbl,"SOC",After="AverageCurrent");
end

参考文献

[1] Kollmeyer, Phillip; Vidal, Carlos; Naguib, Mina; Skells, Michael (2020), "LG 18650HG2 Li-ion Battery Data and Example Deep Neural Network xEV SOC Estimator Script", Mendeley, Data, V3, https://doi.org/10.17632/CP3473X7XV.3.

参考

fitrgp | predict