polyconf

多項式信頼区間

構文

Y = polyconf(p,X)
[Y,DELTA] = polyconf(p,X,S)
[Y,DELTA] = polyconf(p,X,S,param1,val1,param2,val2,...)


説明

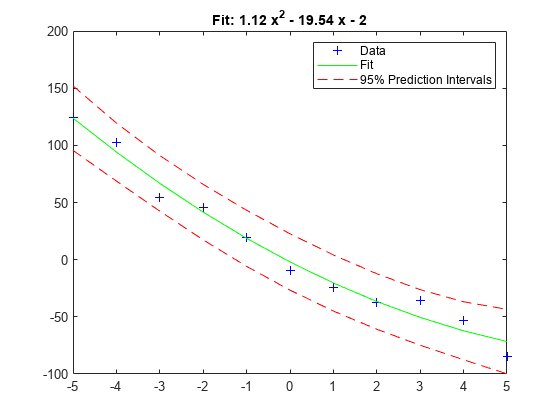
Y = polyconf(p,X) は、X の値における多項式 p を評価します。p は、降べきの順の係数のベクトルです。

[Y,DELTA] = polyconf(p,X,S) は、polyfit の出力 p および S を使用して、X の値の新しい観測値に対する 95% の予測区間 Y ± DELTA を生成します。

[Y,DELTA] = polyconf(p,X,S,param1,val1,param2,val2,...) は、以下のリストから選択されたオプションのパラメーターの名前と値のペアを指定します。

パラメーター	値
'alpha'	100*(1-alpha)% の信頼水準を指定する 0 ～ 1 の範囲の値。既定の設定は 0.05 です。
'mu'	センタリングとスケーリングのパラメーターを含む 2 要素のベクトル。このオプションを指定すると、polyconf は X の代わりに (X-mu(1))/mu(2) を使用します。
'predopt'	X の値における新しい観測値の予測区間を計算するための 'observation' (既定値)、または X の値において評価される近似の信頼区間を計算するための 'curve' のどちらか。以下を参照。
'simopt'	非同時区間に対する 'off' (既定値) または同時区間に対する 'on' のどちらか。以下を参照。

'predopt' および 'simopt' パラメーターの値は、次の関数で表現できます。

• p(x) — 近似により予測される未知の平均関数

• l(x) — 信頼限界の下限

• u(x) — 信頼限界の上限

x_n+1 で新しい観測 y_n+1 を行うとします。

y_n+1(x_n+1) = p(x_n+1) + ε_n+1

既定の設定では、区間 [l_n+1(x_n+1), u_n+1(x_n+1)] は y_n+1(x_n+1) に対する 95% 信頼限界です。

'predopt' および 'simopt' パラメーターの次の組み合わせを使用すると、他の区間を指定できます。

'simopt'	'predopt'	限界区間量
'off'	'observation'	yn+1(xn+1) (既定値)
'off'	'curve'	p(xn+1)
'on'	'observation'	すべての x に対する yn+1(x)
'on'	'curve'	すべての x に対する p(x)

一般的に、'observation' 区間は新しい応答値の予測に不確実性が追加されるため (曲線プラス確率的誤差)、'curve' 区間よりも広くなります。同様に、同時区間はすべての予測子 x に対する区間値の不確かさが加わるため、非同時区間よりも広くなります。

例

多項式近似と予測区間のプロット

多項式を標本データ セットに近似し、95% の予測区間と、近似した多項式の平方根を推定します。データと推定値をプロットし、補助関数 polystr を使用して、近似した多項式を表示します。このコードはこの例の終わりで示します。

標本データ点 (x,y) を 2 次のトレンドと共に生成します。

rng('default') % For reproducibility
x = -5:5;
y = x.^2 - 20*x - 3 + 5*randn(size(x));

polyfitを使用して、2 次多項式をデータに近似します。

degree = 2; % Degree of the fit
[p,S] = polyfit(x,y,degree);

polyconf を使用して、95% の予測区間を推定します。

alpha = 0.05; % Significance level
[yfit,delta] = polyconf(p,x,S,'alpha',alpha);

データ、近似した多項式、および予測区間をプロットします。補助関数 polystr を使用して、近似した多項式を表示します。

plot(x,y,'b+')
hold on
plot(x,yfit,'g-')
plot(x,yfit-delta,'r--',x,yfit+delta,'r--')
legend('Data','Fit','95% Prediction Intervals')
title(['Fit: ',texlabel(polystr(round(p,2)))])
hold off

多項式 p の平方根を求めます。

r = roots(p)

r = 2×1

   17.5152
   -0.1017

平方根は実数値であるため、この値もプロットすることができます。平方根も含めて、x 区間の近似値と予測区間を推定します。次に、平方根と推定値をプロットします。

if isreal(r)
    xmin = min([r(:);x(:)]);
    xrange = range([r(:);x(:)]);
    xExtended = linspace(xmin - 0.1*xrange, xmin + 1.1*xrange,1000);
    [yfitExtended,deltaExtended] = polyconf(p,xExtended,S,'alpha',alpha);

    plot(x,y,'b+')
    hold on
    plot(xExtended,yfitExtended,'g-')
    plot(r,zeros(size(r)),'ko')
    plot(xExtended,yfitExtended-deltaExtended,'r--')
    plot(xExtended,yfitExtended+deltaExtended,'r--')
    plot(xExtended,zeros(size(xExtended)),'k-')
    legend('Data','Fit','Roots of Fit','95% Prediction Intervals')
    title(['Fit: ',texlabel(polystr(round(p,2)))])
    axis tight
    hold off
end

または、対話形式の多項式近似にpolytoolを使用することができます。

polytool(x,y,degree,alpha)

補助関数

補助関数 polystr は polystr.m ファイルで定義されます。

type polystr.m % Display contents of polystr.m file

function s = polystr(p)
% POLYSTR Converts a vector of polynomial coefficients to a character string.
% S is the string representation of P.

if all(p == 0) % All coefficients are 0.
    s = '0';
else
    d = length(p) - 1; % Degree of polynomial.
    s = []; % Initialize s.
    for a = p
        if a ~= 0 % Coefficient is nonzero.
            if ~isempty(s) % String is not empty.
                if a > 0
                    s = [s ' + ']; % Add next term.
                else
                    s = [s ' - ']; % Subtract next term.
                    a = -a; % Value to subtract.
                end
            end
            if a ~= 1 || d == 0 % Add coefficient if it is ~=1 or polynomial is constant.
                s = [s num2str(a)];
                if d > 0 % For nonconstant polynomials, add *.
                    s = [s '*'];
                end
            end
            if d >= 2 % For terms of degree > 1, add power of x.
                s = [s 'x^' int2str(d)];
            elseif d == 1 % No power on x term.
                s = [s 'x'];
            end
        end
        d = d - 1; % Increment loop: Add term of next lowest degree.
    end
end
end

バージョン履歴

R2006a より前に導入

参考

polyfit | polyval | polytool