plotProfileLikelihood
Syntax
Description
plotProfileLikelihood(
specifies additional options using one or more name-value arguments. For example, you can
specify the significance level for the confidence interval and the values for the
coefficient of interest.mdl,coef,Name=Value)
Examples
Load a table of standardized variables generated from the carbig data set.
load standardizedcar.matThe table tbl contains the variables Horsepower, Weight, and MPG, which represent car horsepower, weight, and miles per gallon, respectively.
Fit a nonlinear model to the data using Horsepower and Weight as predictors, and MPG as the response.
modelfun = @(b,x) exp(b(1)*x(:,1))+b(2)*x(:,2)+b(3); beta0 = [0.01 2 -1]; mdl = fitnlm(tbl,modelfun,beta0)
mdl =
Nonlinear regression model:
MPG ~ exp(b1*Horsepower) + b2*Weight + b3
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ ___________
b1 -0.57016 0.045819 -12.444 3.7322e-30
b2 -0.39274 0.043737 -8.9797 1.1804e-17
b3 -1.1417 0.034105 -33.476 1.3291e-116
Number of observations: 392, Error degrees of freedom: 389
Root Mean Squared Error: 0.516
R-Squared: 0.735, Adjusted R-Squared 0.733
F-statistic vs. constant model: 539, p-value = 8.27e-113
mdl contains a fitted nonlinear regression model. The coefficient b1 is a nonlinear coefficient because it is inside the exponential term in the model function.
Plot the profile loglikelihood, coefficient estimate, Wald approximation, and Wald and likelihood-ratio confidence intervals for b1.
plotProfileLikelihood(mdl,"b1")
The plot shows that the maximum likelihood estimate for b1 appears at the peak of the profile loglikelihood, confirming it is the maximum likelihood estimate. The likelihood-ratio confidence interval is slightly wider than the Wald interval, and is also asymmetric. However, the closeness of the two intervals suggests that the assumptions of the Wald approximation hold true for this model.
Load a table of standardized variables generated from the carbig data set.
load standardizedcar.matThe table tbl contains the variables Horsepower, Weight, and MPG, which represent car horsepower, weight, and miles per gallon, respectively.
Fit a nonlinear model to the data using car Horsepower and Weight as predictors, and MPG as the response.
modelfun = @(b,x) exp(b(1)*x(:,1))+b(2)*x(:,2)+b(3); beta0 = [0.01 2 -1]; mdl = fitnlm(tbl,modelfun,beta0)
mdl =
Nonlinear regression model:
MPG ~ exp(b1*Horsepower) + b2*Weight + b3
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ ___________
b1 -0.57016 0.045819 -12.444 3.7322e-30
b2 -0.39274 0.043737 -8.9797 1.1804e-17
b3 -1.1417 0.034105 -33.476 1.3291e-116
Number of observations: 392, Error degrees of freedom: 389
Root Mean Squared Error: 0.516
R-Squared: 0.735, Adjusted R-Squared 0.733
F-statistic vs. constant model: 539, p-value = 8.27e-113
mdl contains a fitted nonlinear regression model.
Plot the profile loglikelihoods for the coefficients without plotting the likelihood-ratio confidence intervals.
tiledlayout(3,1) nexttile plotProfileLikelihood(mdl,"b1",ShowInterval=0) nexttile plotProfileLikelihood(mdl,"b2",ShowInterval=0) nexttile plotProfileLikelihood(mdl,"b3",ShowInterval=0)

The plots show that the profile loglikelihoods are smooth and appear quadratic in nature. Near the coefficient estimates, the Wald intervals are quadratic estimations of the loglikelihood function, so they follow the profile loglikelihood closely.
Load a table of standardized variables generated from the carbig data set.
load standardizedcar.matThe table tbl contains the variables Horsepower, Weight, and MPG, which represent car horsepower, weight, and miles per gallon, respectively.
Fit a nonlinear model to the data using Horsepower and Weight as predictors, and MPG as the response.
modelfun = @(b,x) exp(b(1)*x(:,1))+b(2)*x(:,2)+b(3); beta0 = [0.01 2 -1]; mdl = fitnlm(tbl,modelfun,beta0)
mdl =
Nonlinear regression model:
MPG ~ exp(b1*Horsepower) + b2*Weight + b3
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ ___________
b1 -0.57016 0.045819 -12.444 3.7322e-30
b2 -0.39274 0.043737 -8.9797 1.1804e-17
b3 -1.1417 0.034105 -33.476 1.3291e-116
Number of observations: 392, Error degrees of freedom: 389
Root Mean Squared Error: 0.516
R-Squared: 0.735, Adjusted R-Squared 0.733
F-statistic vs. constant model: 539, p-value = 8.27e-113
mdl contains a fitted nonlinear regression model.
Generate an array of Line objects representing the coefficient estimate, profile loglikelihood, Wald approximation, and 99% Wald and likelihood-ratio confidence intervals for the coefficient b2.
H = plotProfileLikelihood(mdl,"b2",Alpha=0.01)H =
1×5 Line array:
Line Line Line Line Line
H contains five Line objects.
Plot the coefficient estimate in green, the profile loglikelihood and likelihood-ratio interval in black, and the Wald approximation and confidence interval in magenta.
H(1).MarkerFaceColor="g"; % Confidence estimate H(1).MarkerEdgeColor="g"; H(2).Color = "k"; % Profile loglikelihood H(3).Color = "k"; % Likelihood-ratio confidence interval H(4).Color = "m"; % Wald approximation H(5).Color = "m"; % Wald confidence interval
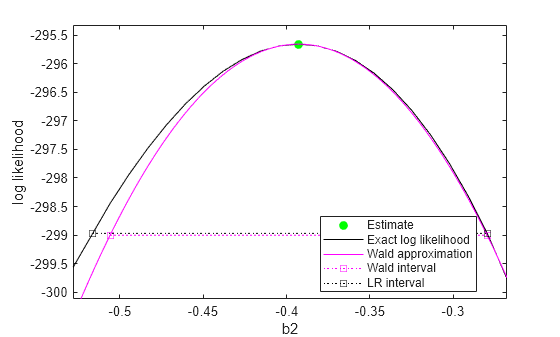
The plot shows that the maximum likelihood estimate for b2 appears at the peak of the profile loglikelihood, confirming it is the maximum likelihood estimate. The likelihood-ratio confidence interval is slightly wider than the Wald interval, and is also asymmetric. However, the closeness of the two intervals suggests that the assumptions of the Wald approximation hold true for this model.
Input Arguments
Nonlinear regression model, specified as a NonLinearModel object created using fitnlm.
Coefficient of interest, specified as a string, character array, or index. Coefficients not
specified in coef are called nuisance coefficients. For each value
of the coefficient of interest, plotProfileLikelihood calculates values for
the nuisance coefficients. For more information, see Profile Loglikelihood.
Example: "b1"
Example: 3
Data Types: single | double | char | string
Target axes, specified as an Axes object. If you do not specify the
axes, then plotProfileLikelihood uses the current axes (gca).
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: plotProfileLikelihood(mdl,"b2",ShowInterval=false,ShowWald=false)
plots only the profile loglikelihood values and the estimate for the coefficient
b2.
Significance level for the confidence intervals, specified as a numeric value in the range [0,1]. The confidence level of CI is equal to 100(1 – alpha)%. Alpha is the probability that the confidence interval does not contain the true value.
Example: Alpha=0.01
Data Types: single | double
Values for the coefficient of interest, specified as a numeric scalar or vector. When you do
not specify CoefficientValues,
plotProfileLikelihood selects values for
coef that cover a typical
confidence interval.
Example: CoefficientValues=[0:0.02:1]
Data Types: single | double
Scale for the loglikelihood values, specified as "linear" or
"log".
When
Scaleis"linear", the function selects values for the coefficient of interest that lie on a Euclidean grid.When
Scaleis"log", the function selects values for the coefficient of interest that lie on a logarithmic grid. You can specifyScaleas"log"only for positive coefficients.
Example: Scale="log"
Data Types: string | char
Flag to show the likelihood-ratio confidence interval in the plot, specified as a
numeric or logical 1 (true) or
0 (false).
Example: ShowInterval=false
Data Types: logical
Flag to show the Wald approximation and confidence interval, specified as a
numeric or logical 1 (true) or
0 (false).
Example:
ShowWald=false
Data Types: logical
Output Arguments
Profile loglikelihood plot lines, returned as a vector of Line
objects. You can modify the properties of the Line objects to customize
the profile plot. The elements of H, in order, are:
Estimate for
coefLoglikelihood profile
Likelihood-ratio confidence interval
Wald approximation
Wald confidence interval
For a complete list of Line properties, see Line Properties.
More About
The profile loglikelihood describes the maximum possible likelihood for a set of nuisance coefficients, given a fixed value of the coefficient of interest. The coefficient of interest is a coefficient that you want to vary, and the nuisance coefficients are the other coefficients in the model formula.
The profile loglikelihood is described by the equation
which contains these variables and terms:
— Coefficient of interest
— Profile loglikelihood function
— Nuisance coefficients
— Predictor input data
— Response input data
— Loglikelihood function for theta given and
Version History
Introduced in R2025a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)