linkage
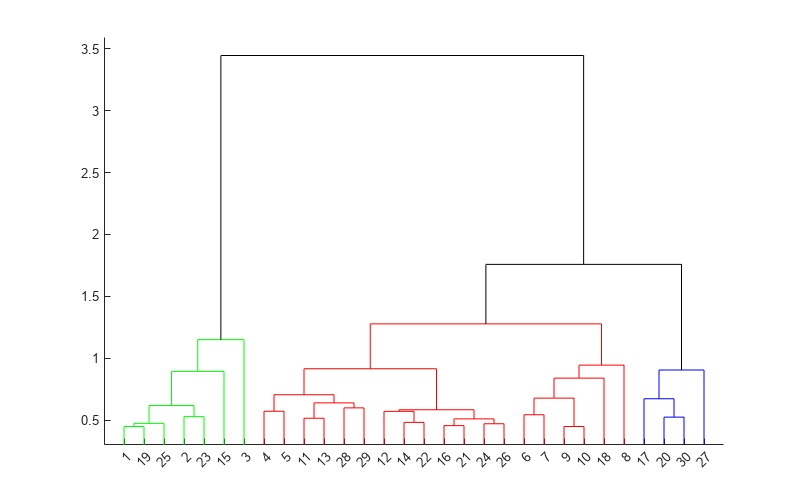
凝集型の階層クラスター ツリー
構文
説明
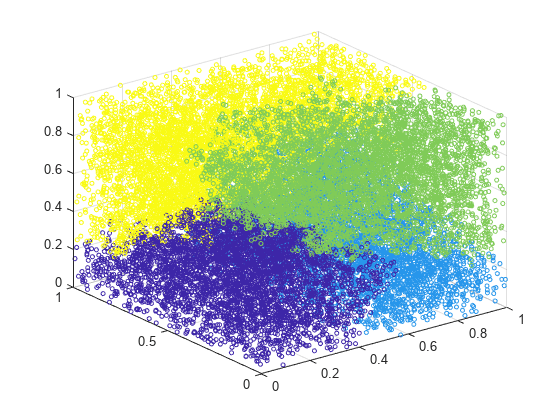
例
入力引数
出力引数
詳細
ヒント
linkage(y)が距離行列のベクトル表現である場合、yの計算速度が低下する可能性があります。'centroid'、'median'、および'ward'メソッドの場合、linkageはyがユークリッド距離かどうかを確認します。時間のかかるチェックを回避するには、yではなくXを渡してください。'centroid'および'median'メソッドは、単調ではないクラスター ツリーを作成できます。このようになるのは、2 つのクラスター r および s の結合から 3 番目のクラスターまでの距離が r と s の間の距離より小さい場合です。この場合、既定の方向に描画したデンドログラムでは、葉からルート ノードへのパスは下向きになります。これを回避するには、別の方法を使用してください。次の図に非単調のクラスター ツリーを示します。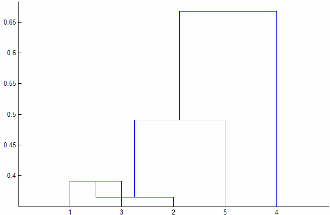
この場合、クラスター 1 とクラスター 3 が結合され新しいクラスターになっていて、この新しいクラスターとクラスター 2 の間の距離はクラスター 1 とクラスター 3 の間の距離よりも短くなっています。これは、非単調なツリーになります。
ツリーを表示する関数
dendrogram、クラスターに点を割り当てる関数cluster、不整合の程度を計算する関数inconsistentおよびコーフェン相関係数を計算する関数cophenetなどを含む、その他の関数に出力Zを提供することができます。
バージョン履歴
R2006a より前に導入
参考
cluster | clusterdata | cophenet | dendrogram | inconsistent | kmeans | pdist | silhouette | squareform