residuals

クラス: GeneralizedLinearMixedModel

当てはめた一般化線形混合効果モデルの残差

構文

r = residuals(glme)

r = residuals(glme,Name,Value)

説明

r = residuals(glme) は、当てはめた一般化線形混合効果モデル glme から条件付きの生の残差を返します。

r = residuals(glme,Name,Value) は、1 つ以上の Name,Value のペアの引数で指定された追加オプションを使用して残差を返します。たとえば、モデルにピアソン残差を返す指定ができます。

入力引数

glme — 一般化線形混合効果モデル

GeneralizedLinearMixedModel オブジェクト

一般化線形混合効果モデル。GeneralizedLinearMixedModel オブジェクトとして指定します。このオブジェクトのプロパティとメソッドについては、GeneralizedLinearMixedModel を参照してください。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

Conditional — 条件付き残差のインジケーター

true (既定値) | false

条件付き残差のインジケーター。'Conditional' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

値	説明
true	固定効果と変量効果の両方からの寄与 (条件付き)
false	固定効果のみからの寄与 (限界)

条件付き残差には、固定効果および変量効果両方の予測子からの寄与が含まれます。限界残差には、固定効果からのみの寄与が含まれます。限界残差の値を得るため、residuals は、変量効果の経験的ベイズの予測子ベクトル b を 0 に設定して、応答の条件付きの平均を計算します。

例: 'Conditional',false

ResidualType — 残差タイプ

'raw' (既定値) | 'Pearson'

残差タイプ。'ResidualType' と、次のいずれかで構成されるコンマ区切りのペアとして指定します。

残差タイプ	条件	限界
'raw'	$$r_{ci}=y_i-g^{-1}\left(x_i^T\widehat{\beta }+z_i^T\widehat{b}+{\delta }_i\right)$$	$$r_{mi}=y_i-g^{-1}\left(x_i^T\widehat{\beta }+{\delta }_i\right)$$
'Pearson'	$$r_{ci}^{pearson}=\frac{r_{ci}}{\sqrt{\frac{\widehat{{\sigma }^2}}{w_i}{v}_i\left({\mu }_i\left(\widehat{\beta },\widehat{b}\right)\right)}}$$	$$r_{mi}^{pearson}=\frac{r_{mi}}{\sqrt{\frac{\widehat{{\sigma }^2}}{w_i}{v}_i\left({\mu }_i\left(\widehat{\beta },0\right)\right)}}$$

以下の各方程式では、

• y_i は n 行 1 列の応答ベクトル y の i 番目の要素です。ここで、i = 1, ..., n です。

• g^-1 はモデルの逆リンク関数です。

• x_i^T は固定効果の計画行列 X の i 番目の行です。

• z_i^T は変量効果の計画行列 Z の i 番目の行です。

• δ_i は i 番目のオフセット値です。

• σ² は分散パラメーターです。

• w_i は i 番目の観測値の重みです。

• v_i は i 番目の観測値の分散項です。

• μ_i は i 番目の観測値の応答の平均です。

• $$\widehat{\beta }$$ と $$\widehat{b}$$ は β と b の推定値です。

一般化線形混合効果モデルの生の残差に、非定数の分散があります。ピアソン残差はほぼ一定の分散であると見込まれ、通常、解析に使用されます。

例: 'ResidualType','Pearson'

出力引数

r — 残差

n 行 1 列のベクトル

n 行 1 列のベクトルとして返される、当てはめた一般化線形混合モデル glme の残差。ここで、n は観測値の数です。

例

残差と当てはめた値の比較のプロット

標本データを読み込みます。

load mfr

このシミュレーションされたデータは、世界中で 50 の工場を操業している製造企業から取得しており、各工場が完成品の生産のためにバッチ処理を実行しています。同社は各バッチの欠陥数を減少させるために新たな製造プロセスを開発しました。新しいプロセスの効果をテストするため、同社は実験に参加させる 20 工場を無作為に選びました。10 工場では新プロセスを実施しますが、残りの 10 工場では旧プロセスの実行を続けます。各 20 工場で、同社は 5 つのバッチ (合計 100 バッチ) を実行し以下のデータを記録しました。

• 新しいプロセスがバッチに使用されたかどうかを示すフラグ (newprocess)

• 各バッチの処理時間。時間単位 (time)

• バッチの温度。摂氏 (temp)

• バッチで使用する化学薬品の供給業者 (A、B または C) を示すカテゴリカル変数 (supplier)

• バッチ内の欠陥数 (defects)

またデータに含まれる time_dev と temp_dev は、摂氏 20 度で 3 時間の標準プロセスから得られる時間と温度の絶対偏差をそれぞれ表します。

固定効果予測子として newprocess、time_dev、temp_dev および supplier を使用して一般化線形混合効果モデルを当てはめます。工場特有の変動に起因して品質に差がある可能性を考慮するために、factory 別にグループ化された切片の変量効果項を含めます。応答変数 defects はポアソン分布であり、このモデルの適切なリンク関数は対数です。係数の予測にラプラス近似メソッドを使用します。ダミー変数エンコードを 'effects' として指定すると、ダミー変数の係数の合計が 0 になります。

欠陥数はポアソン分布を使用してモデル化できます

$${\text{defects}}_{ij}\sim \text{Poisson}({\mu }_{ij})$$

これは一般化線形混合効果モデルに対応します

$$\log ({\mu }_{ij})={\beta }_0+{\beta }_1{\text{newprocess}}_{ij}+{\beta }_2{\text{time}\text{\_}\text{dev}}_{ij}+{\beta }_3{\text{temp}\text{\_}\text{dev}}_{ij}+{\beta }_4{\text{supplier}\text{\_}\text{C}}_{ij}+{\beta }_5{\text{supplier}\text{\_}\text{B}}_{ij}+b_i,$$

ここで

• $${\text{defects}}_{ij}$$ は、バッチ $$j$$ 処理中の工場 $$i$$ で実行されたバッチで観測された欠陥数です。

• $${\mu }_{ij}$$ は、バッチ $$j$$ ($$j=1,2,...,5$$) 処理中の工場 $$i$$ ($$i=1,2,...,20$$) に対応する欠陥の平均数です。

• $${\text{newprocess}}_{ij}$$、$${\text{time}\text{\_}\text{dev}}_{ij}$$ および $${\text{temp}\text{\_}\text{dev}}_{ij}$$ は、バッチ $$j$$ 処理中の工場 $$i$$ に対応する各変数の測定値です。たとえば $${\text{newprocess}}_{ij}$$ は、工場 $$i$$ で実行されたバッチ $$j$$ 処理中に新プロセスが使用されたかどうかを示します。

• $${\text{supplier}\text{\_}\text{C}}_{ij}$$ および $${\text{supplier}\text{\_}\text{B}}_{ij}$$ はエフェクト (ゼロサム) コーディングを使用するダミー変数であり、バッチ $$j$$ 処理中に工場 $$i$$ で実行されたバッチに対して、それぞれ会社 C または B が加工化学薬品を供給したかどうかを示します。

• $$b_i\sim N(0,{\sigma }_b^2)$$ は、工場特有の品質変動に相当する、各工場 $$i$$ の変量効果の切片です。

glme = fitglme(mfr,'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',...
    'Distribution','Poisson','Link','log','FitMethod','Laplace','DummyVarCoding','effects');

条件付きピアソン残差とモデルの条件付きの当てはめた値を生成します。

r = residuals(glme,'ResidualType','Pearson');
mufit = fitted(glme);

ピアソン残差の最初の 10 行を表示します。

r(1:10)

ans = 10×1

    0.4530
    0.4339
    0.3833
   -0.2653
    0.2811
   -0.0935
   -0.2984
   -0.2509
    1.5547
   -0.3027

ピアソン残差と当てはめた値をプロットして残差間の非定数分散の兆候 (不均一分散) を確認します。

figure
scatter(mufit,r)
title('Residuals versus Fitted Values')
xlabel('Fitted Values')
ylabel('Residuals')

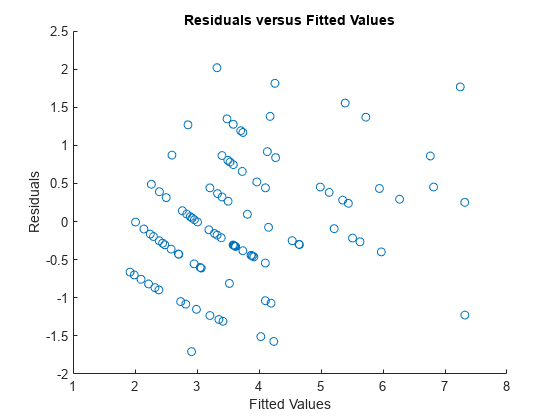
このプロットは当てはめた値において体系的な依存性を示さず、残差間でも非定数分散の兆候がありません。

参考

GeneralizedLinearMixedModel | fitted | response | designMatrix