predict

近傍成分分析 (NCA) 回帰モデルの使用による応答の予測

構文

ypred = predict(mdl,X)

説明

ypred = predict(mdl,X) は、モデル mdl を使用して、X の行に対応する予測応答値 ypred を計算します。

例

loss と predict の使用による回帰用の NCA モデルの調整

標本データを読み込みます。

住宅データ [1] を UCI Machine Learning Repository [2] からダウンロードします。このデータセットには、506 個の観測値が含まれています。最初の 13 列には予測子の値が、最後の列には応答値が含まれています。目標は、ボストン郊外にある持ち家の数の中央値を 13 個の予測子の関数として予測することです。

データを読み込み、応答ベクトルと予測子行列を定義します。

load('housing.data');
X = housing(:,1:13);
y = housing(:,end);

層化区分のグループ化変数として 4 番目の予測子を使用して、データを学習セットとテスト セットに分割します。これにより、各グループから同じ量の観測値が各分割に含まれることが保証されます。

rng(1) % For reproducibility
cvp = cvpartition(X(:,4),'Holdout',56);
Xtrain = X(cvp.training,:);
ytrain = y(cvp.training,:);
Xtest  = X(cvp.test,:);
ytest  = y(cvp.test,:);

cvpartition は、56 個の観測値をテスト セットに、残りのデータを学習セットに無作為に割り当てます。

既定設定の使用による特徴選択の実行

回帰用の NCA モデルを使用して特徴選択を実行します。予測子の値を標準化します。

nca = fsrnca(Xtrain,ytrain,'Standardize',1);

特徴量の重みをプロットします。

figure()
plot(nca.FeatureWeights,'ro')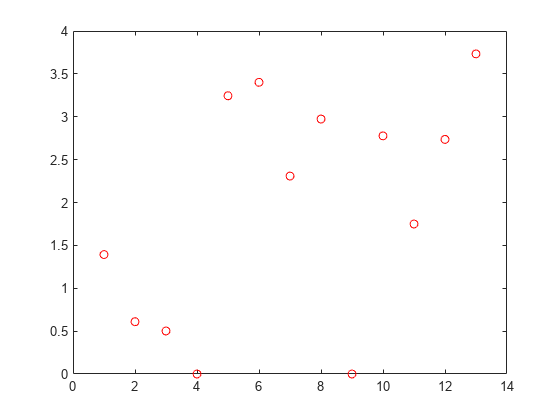

無関係な特徴量の重みはゼロに近くなると考えられます。fsrnca は、2 つの特徴量が無関係であると特定しています。

回帰損失を計算します。

L = loss(nca,Xtest,ytest,'LossFunction','mad')

L = 2.5394

テスト セットについて予測される応答値を計算し、実際の応答に対してプロットします。

ypred = predict(nca,Xtest);
figure()
plot(ypred,ytest,'bo')
xlabel('Predicted response')
ylabel('Actual response')

実際の値に完全に一致すると、45°の直線になります。このプロットでは、予測された応答値と実際の応答値がこの直線の周辺に分布しているように見えます。通常は、$$\lambda$$ (正則化パラメーター) の値を調整すると、性能の改善に役立ちます。

10 分割交差検証の使用による正則化パラメーターの調整

$$\lambda$$ の調整とは、回帰損失が最小になる $$\lambda$$ の値を求めることを意味します。10 分割の交差検証を使用して $$\lambda$$ を調整する手順は次のようになります。

1.はじめに、データを 10 個の分割に分割します。各分割について、cvpartition はデータの 1/10 を学習セットとして、9/10 をテスト セットとして割り当てます。

n = length(ytrain);
cvp = cvpartition(Xtrain(:,4),'kfold',10);
numvalidsets = cvp.NumTestSets;

探索用の $$\lambda$$ の値を割り当てます。損失値を格納する配列を作成します。

lambdavals = linspace(0,2,30)*std(ytrain)/n;
lossvals = zeros(length(lambdavals),numvalidsets);

2.各分割の学習セットを使用して、$$\lambda$$ の各値について近傍成分分析 (NCA) モデルに学習させます。

3.選択された特徴量を使用して、ガウス過程回帰 (GPR) モデルを当てはめます。次に、この GPR モデルを使用して、分割内の対応するテスト セットの回帰損失を計算します。損失の値を記録します。

4.これを $$\lambda$$ の各値および各分割に対して繰り返します。

 for i = 1:length(lambdavals)
    for k = 1:numvalidsets
        X = Xtrain(cvp.training(k),:);
        y = ytrain(cvp.training(k),:);
        Xvalid  = Xtrain(cvp.test(k),:);
        yvalid  = ytrain(cvp.test(k),:);

        nca = fsrnca(X,y,'FitMethod','exact',...
             'Lambda',lambdavals(i),...
             'Standardize',1,'LossFunction','mad');

        % Select features using the feature weights and a relative
        % threshold.
        tol    = 1e-3;
        selidx = nca.FeatureWeights > tol*max(1,max(nca.FeatureWeights));

        % Fit a non-ARD GPR model using selected features.
        gpr = fitrgp(X(:,selidx),y,'Standardize',1,...
              'KernelFunction','squaredexponential','Verbose',0);


        lossvals(i,k) = loss(gpr,Xvalid(:,selidx),yvalid);

    end
 end

$$\lambda$$ の各値について、分割から得られる平均損失を計算します。平均損失と $$\lambda$$ の値をプロットします。

meanloss = mean(lossvals,2);
figure;
plot(lambdavals,meanloss,'ro-');
xlabel('Lambda');
ylabel('Loss (MSE)');
grid on;

損失値が最小になる $$\lambda$$ の値を求めます。

[~,idx] = min(meanloss);
bestlambda = lambdavals(idx)

bestlambda = 0.0251

最適な $$\lambda$$ 値を使用して回帰用の特徴選択を実行します。予測子の値を標準化します。

nca2 = fsrnca(Xtrain,ytrain,'Standardize',1,'Lambda',bestlambda,...
    'LossFunction','mad');

特徴量の重みをプロットします。

figure()
plot(nca.FeatureWeights,'ro')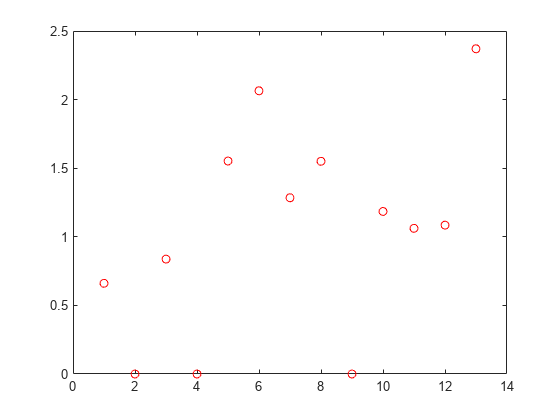

特徴量の選択には使用されなかったテスト データに対して新しい NCA モデルを使用して、損失を計算します。

L2 = loss(nca2,Xtest,ytest,'LossFunction','mad')

L2 = 2.0560

正則化パラメーターの調整は、関連がある特徴量を識別して損失を減らすために役立ちます。

予測された応答値とテスト セット内の実際の応答値をプロットします。

ypred = predict(nca2,Xtest);
figure;
plot(ypred,ytest,'bo');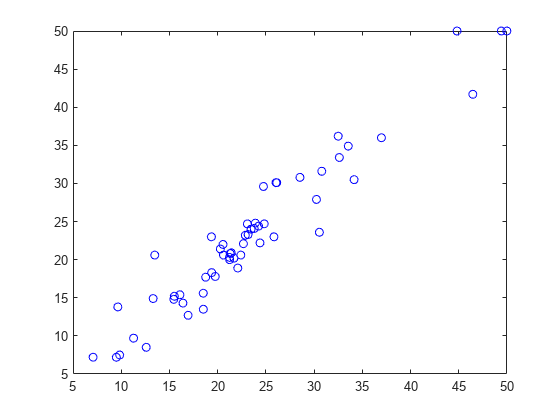

予測された応答値は、実際の値に十分近いように見えます。

参考文献

[1] Harrison, D. and D.L., Rubinfeld. "Hedonic prices and the demand for clean air." J. Environ. Economics & Management. Vol.5, 1978, pp. 81-102.

[2] Lichman, M. UCI Machine Learning Repository, Irvine, CA:University of California, School of Information and Computer Science, 2013. https://archive.ics.uci.edu.

入力引数

mdl — 回帰用の近傍成分分析モデル

FeatureSelectionNCARegression オブジェクト

回帰用の近傍成分分析モデル。FeatureSelectionNCARegression オブジェクトとして指定します。

X — 予測子変数の値

table | n 行 p 列の行列

予測子変数の値。table または n 行 p 列の行列として指定します。ここで、n は観測値の数、p は mdl の学習に使用した予測子変数の数です。既定では、X の各行は 1 つの観測値に対応し、各列は 1 つの変数に対応します。

数値行列の場合

• X の列に含まれている変数の順序は、mdl に学習させた予測子変数の順序と同じでなければなりません。

• table (たとえば Tbl) を使用して mdl に学習させる場合、Tbl に含まれている予測子変数が数値のみであれば、X を数値行列にすることができます。学習時に Tbl 内の数値予測子をカテゴリカルとして扱うには、fsrnca の名前と値の引数 CategoricalPredictors を使用してカテゴリカル予測子を指定します。Tbl に種類の異なる予測子変数 (数値と categorical データ型など) が混在し、X が数値行列である場合、predict でエラーがスローされます。

table の場合

• X には、モデルの学習に使用したすべての予測子が含まれていなければなりません。

• predict は、文字ベクトルの cell 配列ではない cell 配列や複数列の変数をサポートしません。

• table (たとえば Tbl) を使用して mdl に学習させる場合、X 内のすべての予測子変数の変数名およびデータ型が mdl に学習させた (mdl.PredictorNames に格納されている) 変数と同じでなければなりません。ただし、X の列の順序が Tbl の列の順序に対応する必要はありません。また、Tbl と X に追加の変数 (応答変数や観測値の重みなど) を含めることができますが、predict はこれらを無視します。

• 数値行列を使用して mdl に学習させる場合、mdl.PredictorNames 内の予測子名と X 内の対応する予測子変数名が同じでなければなりません。学習時に予測子の名前を指定するには、fsrnca の名前と値の引数 CategoricalPredictors を使用します。X 内の予測子変数はすべて数値ベクトルでなければなりません。X に追加の変数 (応答変数や観測値の重みなど) を含めることができますが、predict はこれらを無視します。

データ型: table | single | double

出力引数

ypred — 予測した応答の値

n 行 1 列のベクトル

予測した応答の値。n 行 1 列のベクトルとして返されます。ここで、n は観測値の数です。

バージョン履歴

R2016b で導入

参考

FeatureSelectionNCARegression | loss | fsrnca | refit | selectFeatures