predict

近傍成分分析 (NCA) 分類器の使用による応答の予測

構文

[labels,postprobs,classnames] = predict(mdl,X)

説明

[labels,postprobs,classnames] = predict(mdl,X) は、モデル mdl を使用して、X の行に対応する予測ラベル labels を計算します。

例

分類用の NCA モデルの調整

標本データを読み込みます。

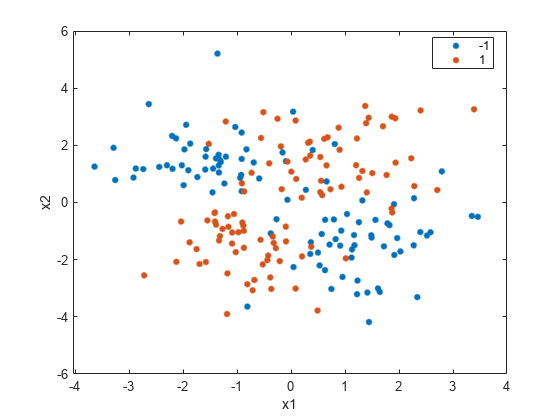
load("twodimclassdata.mat")

このデータ セットは、[1] で説明されている方法を使用してシミュレートしたものです。これは 2 次元の 2 クラス分類問題です。1 番目のクラス (クラス -1) のデータは、2 つの二変量正規分布 $$N({\mu }_1,\Sigma )$$ または $$N({\mu }_2,\Sigma )$$ から同じ確率で抽出されたものです。ここで、$${\mu }_1=[-0.75,-1.5]$$、$${\mu }_2=[0.75,1.5]$$ および $$\Sigma =I_2$$ です。同様に、2 番目のクラス (クラス 1) のデータは、2 つの二変量正規分布 $$N({\mu }_3,\Sigma )$$ または $$N({\mu }_4,\Sigma )$$ から同じ確率で抽出されたものです。ここで、$${\mu }_3=[1.5,-1.5]$$、$${\mu }_4=[-1.5,1.5]$$ および $$\Sigma =I_2$$ です。このデータ セットの作成に使用した正規分布のパラメーターにより、[1] で使用されているデータよりデータのクラスターが緊密になります。

クラス別にグループ化したデータの散布図を作成します。

gscatter(X(:,1),X(:,2),y)
xlabel("x1")
ylabel("x2")

100 個の無関係な特徴量を $$X$$ に追加します。はじめに、平均が 0、分散が 20 の正規分布からデータを生成します。

n = size(X,1);
rng("default")
XwithBadFeatures = [X,randn(n,100)*sqrt(20)];

すべての点が 0 と 1 の間になるようにデータを正規化します。

XwithBadFeatures = (XwithBadFeatures-min(XwithBadFeatures,[],1))./ ...
    range(XwithBadFeatures,1);
X = XwithBadFeatures;

既定値の Lambda (正則化パラメーター $$\lambda$$) を使用して近傍成分分析 (NCA) モデルをデータに当てはめます。LBFGS ソルバーを使用し、収束情報を表示します。

ncaMdl = fscnca(X,y,FitMethod="exact",Verbose=1, ...
    Solver="lbfgs");

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  9.519258e-03 |   1.494e-02 |   0.000e+00 |        |   4.015e+01 |   0.000e+00 |   YES  |
|        1 | -3.093574e-01 |   7.186e-03 |   4.018e+00 |    OK  |   8.956e+01 |   1.000e+00 |   YES  |
|        2 | -4.809455e-01 |   4.444e-03 |   7.123e+00 |    OK  |   9.943e+01 |   1.000e+00 |   YES  |
|        3 | -4.938877e-01 |   3.544e-03 |   1.464e+00 |    OK  |   9.366e+01 |   1.000e+00 |   YES  |
|        4 | -4.964759e-01 |   2.901e-03 |   6.084e-01 |    OK  |   1.554e+02 |   1.000e+00 |   YES  |
|        5 | -4.972077e-01 |   1.323e-03 |   6.129e-01 |    OK  |   1.195e+02 |   5.000e-01 |   YES  |
|        6 | -4.974743e-01 |   1.569e-04 |   2.155e-01 |    OK  |   1.003e+02 |   1.000e+00 |   YES  |
|        7 | -4.974868e-01 |   3.844e-05 |   4.161e-02 |    OK  |   9.835e+01 |   1.000e+00 |   YES  |
|        8 | -4.974874e-01 |   1.417e-05 |   1.073e-02 |    OK  |   1.043e+02 |   1.000e+00 |   YES  |
|        9 | -4.974874e-01 |   4.893e-06 |   1.781e-03 |    OK  |   1.530e+02 |   1.000e+00 |   YES  |
|       10 | -4.974874e-01 |   9.404e-08 |   8.947e-04 |    OK  |   1.670e+02 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 9.404e-08
              Two norm of the final step     = 8.947e-04, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 9.404e-08, TolFun = 1.000e-06
EXIT: Local minimum found.

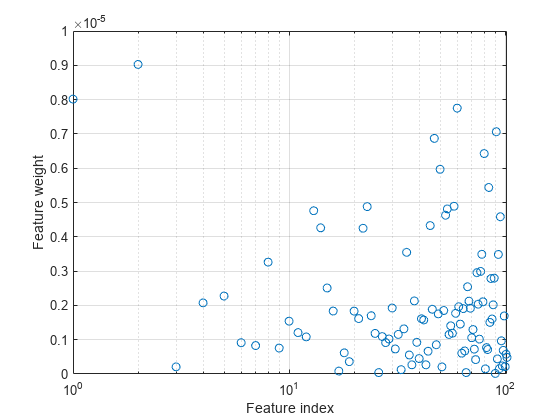
特徴量の重みをプロットします。無関係な特徴量の重みはゼロに非常に近いはずです。

semilogx(ncaMdl.FeatureWeights,"o")
xlabel("Feature index")
ylabel("Feature weight")    
grid on

NCA モデルを使用してクラスを予測し、混同行列を計算します。

ypred = predict(ncaMdl,X);
confusionchart(y,ypred)

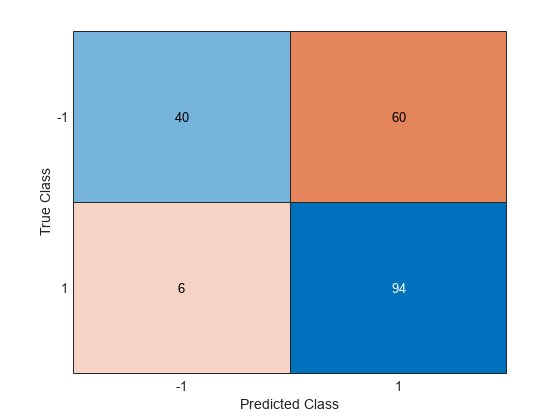
混同行列は、クラス –1 に属しているデータのうち 40 個がクラス –1 に属すという予測を示しています。クラス –1 のデータのうち 60 個は、クラス 1 に属すことが予測されています。同様に、クラス 1 のデータのうち 94 個はクラス 1 に、6 個はクラス –1 に属すことが予測されています。クラス -1 の予測精度が良くありません。

すべての重みがゼロに非常に近くなっています。これは、モデルに学習させるときに使用した $$\lambda$$ の値が大きすぎることを示します。$$\lambda \to \infty$$ では、すべての特徴量の重みがゼロに近づきます。したがって、関連がある特徴量を判別するには、ほとんどのケースで正則化パラメーターを調整することが重要です。

5 分割交差検証を使用して、fscnca を使用する特徴選択用に $$\lambda$$ を調整します。$$\lambda$$ の調整とは、分類損失が最小になる $$\lambda$$ の値を求めることを意味します。交差検証を使用して $$\lambda$$ を調整するため、以下を行います。

1.データを 5 つの分割に分割します。各分割について、cvpartition はデータの 4/5 を学習セットとして、1/5 をテスト セットとして割り当てます。さらに各分割について、クラスの比率がほぼ等しい層化区分を cvpartition で作成します。

cvp = cvpartition(y,"KFold",5);
numtestsets = cvp.NumTestSets;
lambdavalues = linspace(0,2,20)/length(y); 
lossvalues = zeros(length(lambdavalues),numtestsets);

2.各分割の学習セットを使用して、$$\lambda$$ の各値について近傍成分分析 (NCA) モデルに学習させます。

3.NCA モデルを使用して、分割内の対応するテスト セットの分類損失を計算します。損失の値を記録します。

4.このプロセスをすべての分割およびすべての $$\lambda$$ の値に対して繰り返します。

for i = 1:length(lambdavalues)                
    for k = 1:numtestsets
        
        % Extract the training set from the partition object
        Xtrain = X(cvp.training(k),:);
        ytrain = y(cvp.training(k),:);
        
        % Extract the test set from the partition object
        Xtest  = X(cvp.test(k),:);
        ytest  = y(cvp.test(k),:);
        
        % Train an NCA model for classification using the training set
        ncaMdl = fscnca(Xtrain,ytrain,FitMethod="exact", ...
            Solver="lbfgs",Lambda=lambdavalues(i));
        
        % Compute the classification loss for the test set using the NCA
        % model
        lossvalues(i,k) = loss(ncaMdl,Xtest,ytest, ...
            LossFunction="quadratic");   
   
    end                          
end

分割の平均損失値を $$\lambda$$ の値についてプロットします。最小の損失に対応する $$\lambda$$ の値が $$\lambda$$ のテスト済みの値の境界に位置する場合、$$\lambda$$ の値の範囲を再検討する必要があります。

plot(lambdavalues,mean(lossvalues,2),"o-")
xlabel("Lambda values")
ylabel("Loss values")
grid on

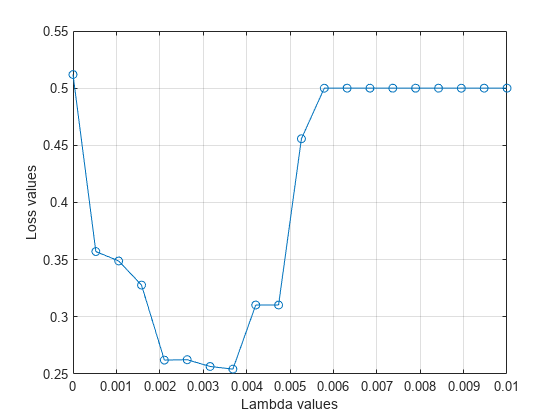
最小の平均損失に対応する $$\lambda$$ の値を求めます。

[~,idx] = min(mean(lossvalues,2)); % Find the index
bestlambda = lambdavalues(idx) % Find the best lambda value

bestlambda = 
0.0037

最適な $$\lambda$$ の値を使用して、すべてのデータに NCA モデルを当てはめます。LBFGS ソルバーを使用し、収束情報を表示します。

ncaMdl = fscnca(X,y,FitMethod="exact",Verbose=1, ...
    Solver="lbfgs",Lambda=bestlambda);

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 | -1.246913e-01 |   1.231e-02 |   0.000e+00 |        |   4.873e+01 |   0.000e+00 |   YES  |
|        1 | -3.411330e-01 |   5.717e-03 |   3.618e+00 |    OK  |   1.068e+02 |   1.000e+00 |   YES  |
|        2 | -5.226111e-01 |   3.763e-02 |   8.252e+00 |    OK  |   7.825e+01 |   1.000e+00 |   YES  |
|        3 | -5.817731e-01 |   8.496e-03 |   2.340e+00 |    OK  |   5.591e+01 |   5.000e-01 |   YES  |
|        4 | -6.132632e-01 |   6.863e-03 |   2.526e+00 |    OK  |   8.228e+01 |   1.000e+00 |   YES  |
|        5 | -6.135264e-01 |   9.373e-03 |   7.341e-01 |    OK  |   3.244e+01 |   1.000e+00 |   YES  |
|        6 | -6.147894e-01 |   1.182e-03 |   2.933e-01 |    OK  |   2.447e+01 |   1.000e+00 |   YES  |
|        7 | -6.148714e-01 |   6.392e-04 |   6.688e-02 |    OK  |   3.195e+01 |   1.000e+00 |   YES  |
|        8 | -6.149524e-01 |   6.521e-04 |   9.934e-02 |    OK  |   1.236e+02 |   1.000e+00 |   YES  |
|        9 | -6.149972e-01 |   1.154e-04 |   1.191e-01 |    OK  |   1.171e+02 |   1.000e+00 |   YES  |
|       10 | -6.149990e-01 |   2.922e-05 |   1.983e-02 |    OK  |   7.365e+01 |   1.000e+00 |   YES  |
|       11 | -6.149993e-01 |   1.556e-05 |   8.354e-03 |    OK  |   1.288e+02 |   1.000e+00 |   YES  |
|       12 | -6.149994e-01 |   1.147e-05 |   7.256e-03 |    OK  |   2.332e+02 |   1.000e+00 |   YES  |
|       13 | -6.149995e-01 |   1.040e-05 |   6.781e-03 |    OK  |   2.287e+02 |   1.000e+00 |   YES  |
|       14 | -6.149996e-01 |   9.015e-06 |   6.265e-03 |    OK  |   9.974e+01 |   1.000e+00 |   YES  |
|       15 | -6.149996e-01 |   7.763e-06 |   5.206e-03 |    OK  |   2.919e+02 |   1.000e+00 |   YES  |
|       16 | -6.149997e-01 |   8.374e-06 |   1.679e-02 |    OK  |   6.878e+02 |   1.000e+00 |   YES  |
|       17 | -6.149997e-01 |   9.387e-06 |   9.542e-03 |    OK  |   1.284e+02 |   5.000e-01 |   YES  |
|       18 | -6.149997e-01 |   3.250e-06 |   5.114e-03 |    OK  |   1.225e+02 |   1.000e+00 |   YES  |
|       19 | -6.149997e-01 |   1.574e-06 |   1.275e-03 |    OK  |   1.808e+02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       20 | -6.149997e-01 |   5.764e-07 |   6.765e-04 |    OK  |   2.905e+02 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 5.764e-07
              Two norm of the final step     = 6.765e-04, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 5.764e-07, TolFun = 1.000e-06
EXIT: Local minimum found.

特徴量の重みをプロットします。

semilogx(ncaMdl.FeatureWeights,"o")
xlabel("Feature index")
ylabel("Feature weight")    
grid on

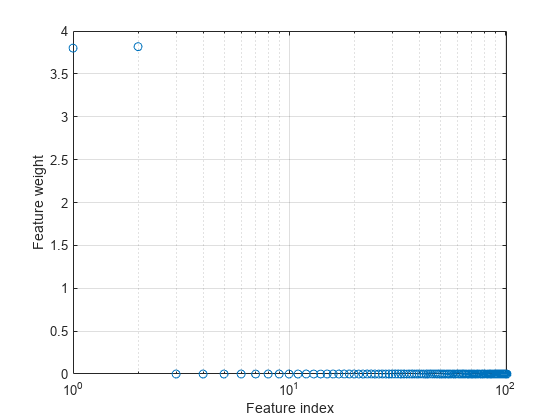
fscnca は、初めの 2 つの特徴量に関連があり残りはそうではないことを正しく判別します。初めの 2 つの特徴量は単独では情報を与えませんが、一緒にすると正確な分類モデルが得られます。

新しいモデルを使用してクラスを予測し、精度を計算します。

ypred = predict(ncaMdl,X);
confusionchart(y,ypred)

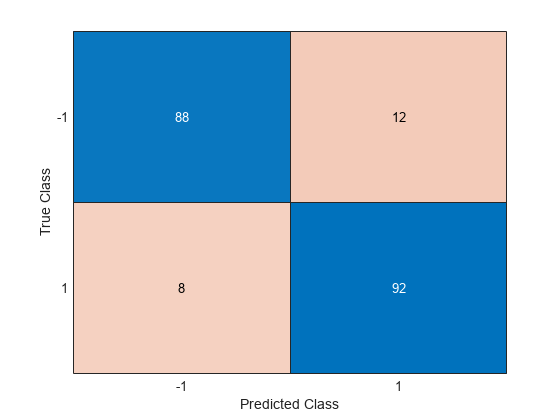
混同行列は、クラス -1 の予測精度が改善されたことを示しています。クラス –1 のデータのうち 88 個はクラス –1 に、12 個はクラス 1 に属すことが予測されています。また、クラス 1 のデータのうち 92 個はクラス 1 に、8 個はクラス –1 に属すことが予測されています。

参考文献

[1] Yang, W., K. Wang, W. Zuo."Neighborhood Component Feature Selection for High-Dimensional Data." Journal of Computers. Vol. 7, Number 1, January, 2012.

入力引数

mdl — 分類用の近傍成分分析モデル

FeatureSelectionNCAClassification オブジェクト

分類用の近傍成分分析モデル。FeatureSelectionNCAClassification オブジェクトとして指定します。

X — 予測子変数の値

table | n 行 p 列の行列

予測子変数の値。table または n 行 p 列の行列として指定します。ここで、n は観測値の数、p は mdl の学習に使用した予測子変数の数です。

既定では、X の各行は 1 つの観測値に対応し、各列は 1 つの変数に対応します。

数値行列の場合

• X の列に含まれている変数の順序は、mdl に学習させた予測子変数の順序と同じでなければなりません。

• table (たとえば Tbl) を使用して mdl に学習させる場合、Tbl に含まれている予測子変数が数値のみであれば、X を数値行列にすることができます。学習時に Tbl 内の数値予測子をカテゴリカルとして扱うには、fscnca の名前と値の引数 CategoricalPredictors を使用してカテゴリカル予測子を指定します。Tbl に種類の異なる予測子変数 (数値と categorical データ型など) が混在し、X が数値行列である場合、predict でエラーがスローされます。

table の場合

• predict は、文字ベクトルの cell 配列ではない cell 配列や複数列の変数をサポートしません。

• table (たとえば Tbl) を使用して mdl に学習させる場合、X 内のすべての予測子変数の変数名およびデータ型が mdl に学習させた (mdl.PredictorNames に格納されている) 変数と同じでなければなりません。ただし、X の列の順序が Tbl の列の順序に対応する必要はありません。また、Tbl と X に追加の変数 (応答変数や観測値の重みなど) を含めることができますが、predict はこれらを無視します。

• 数値行列を使用して mdl に学習させる場合、mdl.PredictorNames 内の予測子名と X 内の対応する予測子変数名が同じでなければなりません。学習時に予測子の名前を指定するには、fscnca の名前と値の引数 CategoricalPredictors を使用します。X 内の予測子変数はすべて数値ベクトルでなければなりません。X に追加の変数 (応答変数や観測値の重みなど) を含めることができますが、predict はこれらを無視します。

データ型: table | single | double

出力引数

labels — 予測クラス ラベル

categorical ベクトル | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列 | 文字配列

X の行に対応する予測クラス ラベル。長さ n の categorical ベクトル、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列、あるいは n 行の文字配列として返されます。n は観測値の個数です。labels は、学習に使用した ResponseName または Y と同じ型になります。

postprobs — 事後確率

n 行 c 列の行列

事後確率。n 行 c 列の行列として返されます。n は観測値の個数、c はクラスの個数です。事後確率 postprobs(i,:) は、クラス 1 ～ c における、X(i,:) 内の観測値のメンバーシップを表します。

classnames — クラス名

文字ベクトルの cell 配列

事後確率に対応するクラスの名前。文字ベクトルの cell 配列として返されます。各文字ベクトルは、postprobs の列に対応するクラスの名前です。

バージョン履歴

R2016b で導入

参考

FeatureSelectionNCAClassification | fscnca | loss | refit | selectFeatures