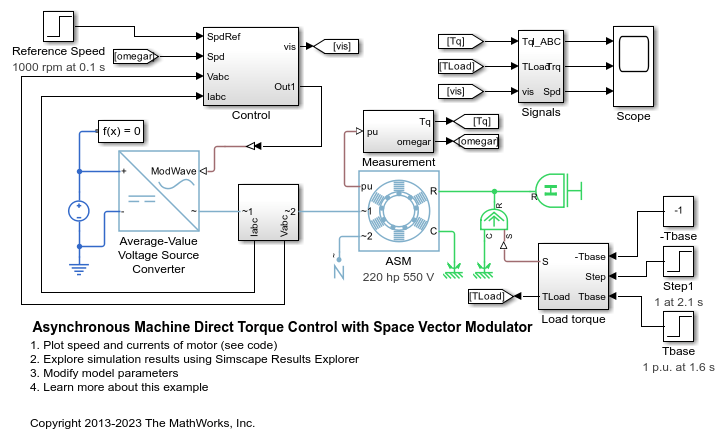
Average-Value Voltage Source Converter (Three-Phase)
Three-phase average-value bidirectional AC/DC voltage source converter
Libraries:
Simscape /
Electrical /
Semiconductors & Converters /
Converters
Description
The Average-Value Voltage Source Converter (Three-Phase) block converts electrical energy from AC to DC voltage or from DC to AC voltage according to an input three-phase modulation wave. You can specify the modulation wave directly or through phasor quantities such as the magnitude and phase shift. The corresponding input power is equal to the sum of the fixed power loss and the output power.
This block can work in both time and frequency-and-time simulation modes. If you set the
AC frequency parameter to Variable,
this block works only in time simulation mode. If you select
Constant, this block works in both time and
frequency-time simulation modes. For more information, see Frequency and Time Simulation Mode.
Losses Parameterization
Switching losses, conduction losses, and quiescent losses are the main heat sources for a converter.
The switching losses are defined by this equation:
where:
ks is the proportionality constant that depends on the turn-on and turn-off intervals and switching frequency. Specify this value by setting the Switching losses coefficient, ks parameter.
vdc is the dc-link voltage.
is the root mean square (RMS) phase current, where
The conduction losses are defined by this equation:
where:
kc1 is the coefficient of the conduction losses that depends on the on-state zero current collector-emitter voltage of the transistor and on the forward voltage drop of the diode. Specify this value by setting the Conduction losses coefficient, kc1 parameter.
kc2 is the coefficient of the conduction losses that depends on the state resistance of the transistor and on the anti-parallel diode. Specify this value by setting the Conduction losses coefficient, kc2 parameter.
The quiescent losses are defined by the Fixed power loss parameter, Pfixed.
The sum of the switching, conduction, and quiescent losses define the total power losses of the converter:
If not available, you can also obtain the
ks,
kc1,
kc2 and
Pfixed parameters values from the
power losses profile, by setting the Losses parameterization
parameter to Profile: loss=f(Irms,vdc_nom). The block
then solves this equation and calculates the values of the parameters:
where is the vector of power loss values, Converter losses, corresponding to the RMS current for converter losses parameter, , and the Nominal dc-link voltage, vdc_nom.
Model Thermal Effects
This block has one optional thermal port. To control the visibility of the thermal port, set the Modeling option parameter to either:
No thermal port— The block does not contain a thermal port.Show thermal port— The block contains one thermal conserving port.
Examples
Ports
Input
Conserving
Parameters
References
[1] M. N., Rajput. "Thermal modeling of permanent magnet synchronous motor and inverter." Master's Thesis, Georgia Institute of Technology, 2016. https://hdl.handle.net/1853/55053.