極値探索制御

極値探索制御 (ESC) は、モデルに依存しないリアルタイムの適応制御アルゴリズムであり、不明なシステムダイナミクスや制御パラメーターから目的関数への不明なマッピングにパラメーターを適応させる場合に役立ちます。極値探索を使用して、静的最適化の問題を解決したり、動的システムのパラメーターを最適化したりできます。

極値探索アルゴリズムでは、次の段階を使用してパラメーター値を調整します。

変調 — 最適化するパラメーターの値に低振幅の正弦波信号を使用して摂動を加えます。
システム応答 — 最適化するシステムがパラメーターの摂動に反応します。この反応に基づいて、目的関数の値が対応して変化します。
復調 — 目的関数の信号に変調信号と同じ周波数の正弦波を乗算します。この段階には、オプションとして、目的関数の信号からバイアスを除去するハイパスフィルターが含まれます。
パラメーター更新 — 復調された信号を積分してパラメーター値を更新します。パラメーター値は積分器の状態に対応します。この段階には、オプションとして、復調された信号から高周波数のノイズを除去するローパスフィルターが含まれます。

Simulink^® Control Design™ ソフトウェアでは、このアルゴリズムを Extremum Seeking Control ブロックを使用して実装しています。極値探索制御の例については、以下を参照してください。

時間領域

Extremum Seeking Control ブロックを使用して、連続時間と離散時間の両方のコントローラーを実装できます。ESC アルゴリズムはどちらの場合も同じです。コントローラーの時間領域を変更すると、調整ループで使用されるハイパスフィルター、ローパスフィルター、および積分器の時間領域に影響します。

ハードウェアに展開可能な Extremum Seeking Control ブロックのコードを生成するには、離散時間コントローラーを使用してください。

次の表に、Extremum Seeking Control ブロックにおけるフィルターと積分器の連続時間および離散時間の伝達関数を示します。

コントローラー要素	連続時間の伝達関数	離散時間の伝達関数
ハイパスフィルター	$\frac{s}{s + ω_{h}}$	$\frac{1 - z^{- 1}}{1 - ω_{h} z^{- 1}}$
ローパスフィルター	$\frac{1}{s + ω_{l}}$	$\frac{1}{1 - ω_{l} z^{- 1}}$
積分器	$\frac{1}{s}$	前進型オイラー: $\frac{T_{s}}{z - 1}$ 後退型オイラー: $\frac{T_{s} z}{z - 1}$ 台形則: $\frac{T_{s}}{2} \frac{z + 1}{z - 1}$

コントローラー要素

連続時間の伝達関数

離散時間の伝達関数

ハイパスフィルター

$\frac{s}{s + ω_{h}}$

$\frac{1 - z^{- 1}}{1 - ω_{h} z^{- 1}}$

ローパスフィルター

$\frac{1}{s + ω_{l}}$

$\frac{1}{1 - ω_{l} z^{- 1}}$

積分器

$\frac{1}{s}$

前進型オイラー:

$\frac{T_{s}}{z - 1}$

後退型オイラー:

$\frac{T_{s} z}{z - 1}$

台形則:

$\frac{T_{s}}{2} \frac{z + 1}{z - 1}$

ここで

ω_l はローパスフィルターのカットオフ周波数です。
ω_h はハイパスフィルターのカットオフ周波数です。
T_s は離散時間コントローラーの学習率のサンプル時間です。

静的最適化

極値探索のデモとして、次の静的最適化の問題について考えます。

Extremum seeking control diagram showing the modulation, demodulation, and parameter update stages.

ここで

$\hat{θ}$ は推定パラメーター値です。
θ は変調信号です。
y = f(θ) は最大化する関数出力、つまり目的関数です。
ω は変調信号と復調信号の強制周波数です。
b·sin(ωt) は変調信号です。
a·sin(ωt) は復調信号です。
k は学習率です。

最適なパラメーター値 θ* は、f(θ) の値が最大のときの値です。

複数のパラメーターを最適化するには、パラメーターごとに別々の調整ループを使用します。

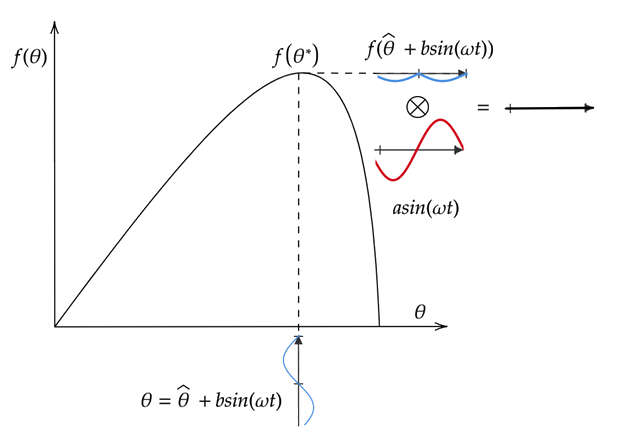
次の図は、目的関数の曲線の "増加部分" についての極値探索を示しています。変調された信号 θ は、現在の推定パラメーターと変調信号の合計です。f(θ) を適用して摂動を加えると、変調信号と同じ位相の目的関数が生成されます。摂動を加えられた目的関数に復調信号を乗算すると、正の信号が生成されます。この信号を積分すると、θ の値が増加し、目的関数のピークに近づきます。

Graph of an objective function with modulation and demodulation demonstrated on an increasing portion of the curve.

次の図は、目的関数の曲線の "減少部分" についての極値探索を示しています。この場合、f(θ) を適用して摂動を加えると、変調信号から位相が 180 度ずれた目的関数が生成されます。復調信号を乗算すると、負の信号が生成されます。この信号を積分すると、θ の値が減少し、目的関数のピークに近づきます。

Graph of an objective function with modulation and demodulation demonstrated on a decreasing portion of the curve

次の図は、目的関数の曲線の "フラットな部分"、つまり曲線の最大に近い部分についての極値探索を示しています。この場合、f(θ) を適用して摂動を加えると、ゼロに近い目的関数が生成されます。復調信号を乗算してこの信号を積分しても θ の値に大きな変化はなく、既に最適な値である θ* に近い値になります。

Graph of an objective function with modulation and demodulation demonstrated on a nearly flat portion of the curve

動的システムの最適化

極値探索による動的システムの最適化も静的最適化と同じようになります。ただし、この場合は、パラメーター θ が時間依存の動的システムの出力に影響します。最大化する目的関数はシステムの出力から計算されます。次の図に、動的システムについての一般的な調整ループを示します。

Extremum seeking for a time-dependent dynamic system.

ここで

$\dot{x} = f (x, α (x, θ))$ は動的システムのステート関数です。
z = h(x) は動的システムの出力です。
y = g(z) は動的システムの出力から導出された目的関数です。
ϕ₁ は復調信号の位相です。
ϕ₂ は変調信号の位相です。

ESC の設計ガイドライン

極値探索コントローラーを設計するときは、次のガイドラインを考慮してください。

必ずシステムダイナミクスの時間スケールが最も高速で、強制周波数の時間スケールが中間、フィルターのカットオフ周波数の時間スケールが最も低速になるようにします。
復調信号の振幅が変調信号の振幅よりも十分に大きく (a ≫ b) なるように振幅を指定します。
変調信号と復調信号の位相角が cos(ϕ₁ – ϕ₂) > 0 となるように位相角を選択します。
複数のパラメーターを調整する場合、調整ループごとに強制周波数が異なっていなければなりません。
ハイパスフィルターとローパスフィルターがないシステムの設計を最初に試します。その後、満足な性能が得られない場合に一方または両方のフィルターの追加を検討できます。

参照

[1] Ariyur, Kartik B., and Miroslav Krstić. Real Time Optimization by Extremum Seeking Control. Hoboken, NJ: Wiley Interscience, 2003.

参考

ブロック

Extremum Seeking Control