システムとモデル

このトピックでは、Simulink^® ソフトウェアのツールを使用する上での一貫した共通言語を提供する概念を示します。

システム

"システム" は、時間と共に変化する測定可能な特性をもった相互に依存する物理的および機能的なパーツのグループです。

たとえば、車両は複数のパーツをもつ "システム" です。測定可能な特性には、車両の直線運動の速度とホイールの回転の速度が含まれます。

システム コンポーネント

"システム コンポーネント" は、"システム" の他のパーツと作用する "システム" のパーツです。コンポーネント間の交互作用は、"システム" の構造と動作を定義します。

たとえば、クルーズ コントロール モジュールは、車両 "システム" の "システム コンポーネント" です。マイクロコントローラーとそれに関連するハードウェアでは構造体を定義し、速度を制御するソフトウェア アルゴリズムで動作を定義します。

モデル

"モデル" は、物理法則または実験データから得られる "システム" の数学的な記述です。記述では、通常、一連の変数と共にそれらの変数間の関係を定義する一連の微分方程式と差分方程式が使用されます。

車両の次の例では、u(t) は車両を前進させる力 (N)、v(t) は速度 (m/s)、b は抵抗係数 (Nׂׂ·s/m)、および m は車両の質量 (kg) です。

車両は連続システムです。連続システムの場合、微分方程式は変数の変化率をすべての時間の値に対して定義された方程式を使用して記述します。車両 v(t) の速度とその加速度 v'(t) は、次の 1 階微分方程式で定義されます。

mv'(t) + bv(t) = u(t)

ブロックを追加して、ブロックの動作を指定し、信号線を使用してブロックを相互に接続することで、この方程式の Simulink モデルを作成できます。次の Simulink "ブロック線図" は、この微分方程式を実装したものです。

モデル コンポーネント

"モデル コンポーネント" は、入出力のインターフェイスを通じて他のパーツと作用する "モデル" のパーツです。Simulink では、Subsystem ブロックと Model ブロックを使用して、"モデル コンポーネント" を実装します。Model ブロックは、別のファイルに保存された別の Simulink モデルを参照します。

次の例では、制御モデルが Simulink モデル ファイル control_model.slx に保存された後、2 つ目の Simulink モデルの Model ブロックから参照されています。Subsystem ブロックは、車両構造をモデル化するために追加されました。

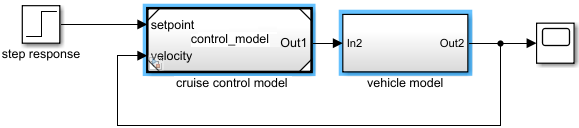
通常、コントローラーは、コンピューターを使用して制御アルゴリズムを実装する離散システムで組み込まれます。離散システムの場合、差分方程式は、特定の時間に対してのみ定義される変数の変化率を記述します。たとえば、単純な離散 PI (比例-積分形) コントローラーの制御信号は、次の差分方程式で定義されます。

PI[n] = e[n]Kp + (e[n]+integral[n-1])Ki

ここで、e[n] は、値が制御されている信号 (速度) と指定値 (設定速度) 間の誤差、Kp は比例定数、Ki は積分定数、n はタイム ステップです。

次の Simulink "ブロック線図" は、この差分方程式を実装したものです。

参考: 簡単な連続システムのモデル作成、コンポーネントベースのモデル化のガイドライン、カスタム ライブラリの作成、モデル参照の基礎。

微分代数方程式

連立方程式には、微分方程式に加えて、独立変数と状態ベクトルに関する追加の制約を含むものがあります。このような方程式を "微分代数方程式" (DAE) と呼びます。

"代数" は微分係数を含まない方程式を意味します。

Simulink モデルでは、代数ループは代数制約を表します。代数ループを含むモデルは、微分代数方程式系を定義します。

たとえば、単純な DAE 系を実装する次のモデルを考えます。内側のループは代数制約を表し、外側のループは微分方程式を表しています。

このモデルでは次の DAE 系が実装されます。

x' = x_a

0 = u - x - 2x_a