Simulink シミュレーション
動的システムのモデルをシミュレートすることで、時間をかけてシステムを実際に構築しなくても、推奨されるシステム設計の動作について考察することができます。このトピックでは、Simulink® ソフトウェアのツールでモデルのシミュレーションを制御する方法について理解するためのコンテキストを提供する概念を示します。
コンパイル
コンパイルは、"ブロック線図" を Simulink エンジンと連携する内部表現に変換する Simulink のプロセスです。
全体として数値の解を求める微分方程式のモデルレベルのセットはありません。代わりに、モデルレベルの方程式は、特定の順序で数値の解を求める個々のブロック方程式を表します。
ブロックのメソッド
単一ブロックの機能は、複数の方程式で定義されます。これらの式は、ブロックのメソッドとして表されます。これらのブロックのメソッドは、ブロック線図の実行中に評価 (実行) されます。これらのブロックのメソッドの評価は、シミュレーション ループ内で行われ、シミュレーション ループの各サイクルは、各時点でのブロック線図の評価を表します。共通のブロックのメソッドは次のとおりです。
Derivative – ブロックの入力と前のタイム ステップでの状態の値から、現在のタイム ステップでのブロックの連続状態の導関数を計算
Update – 現在のタイム ステップでの入力と前のタイム ステップでの離散状態から、現在のタイム ステップでのブロックの離散状態の値を計算
Output – 現在のタイム ステップでの入力と前のタイム ステップでの状態からブロックの出力を計算

モデルのメソッド
ブロックのメソッドに加えて、モデルのプロパティとその出力を計算する一連のメソッドも提供されています。Simulink ソフトウェアは、モデルのプロパティと出力を決定するために、シミュレーション中に同様にこれらのメソッドを呼び込みます。モデルのメソッドは、一般に、同じタイプのブロックのメソッドを呼び込むことによってこれらの作業を行います。たとえば、モデルの Outputs メソッドは、出力を計算するためにモデルによって指定される順番で、含んでいるブロックの Outputs メソッドを呼び込みます。モデルの Derivatives メソッドは、同様に、状態の導関数を決定するために、含んでいるブロックの Derivatives メソッドを呼び込みます。
参考: 動的システムのシミュレーションの段階。
コールバック
コールバックは、特定のモデリング アクションに応じて実行される MATLAB® 式です。Simulink は、ある種のモデリング アクションを識別するモデル、ブロック、および端子のコールバック パラメーターを提供します。コールバック パラメーターには、コードを与えます。このコードは、関連するモデリング アクションが発生したときに、Simulink が実行します。
モデル コールバック
モデル コールバック パラメーターは次のとおりです。
PreloadFcn– モデルの読み込み前に実行されます。たとえば、モデルが使用する変数値を MATLAB ワークスペースに読み込むコードを指定できます。
モデル コールバックを参照してください。
ブロックのコールバック
ブロックのコールバック パラメーターは次のとおりです。
OpenFcn– Subsystem ブロックを開くと実行されます。LoadFcn– ブロック線図が読み込まれた後に実行されます。Subsystem ブロックの場合は、Subsystem ブロック内のブロックに対してもブロックのコールバック パラメーターを実行します。
端子のコールバック
端子のコールバック パラメーターは次のとおりです。
ConnectionCallback- 端子の接続が変更されるたびにコードが実行されます。
端子のコールバックを参照してください。
実行順序
実行順序は、各入力端子の直達を評価した後にブロック出力メソッドが呼び出される順序です。実行順序を表示するには、[デバッグ] タブで、[情報のオーバーレイ] 、 [実行順序]を選択します。
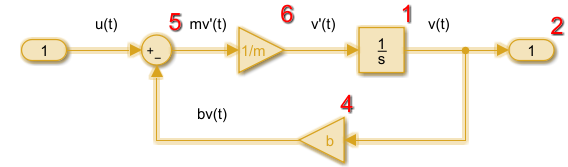
以下のモデルでは、Integrator ブロック出力が最初に実行され、次に Integrator ブロック入力に接続されたブロックのループが実行されます。シーケンスの実行番号が欠落するのは、通常、いわゆる "非表示バッファー" ブロックが原因です。出力端子がバーチャルであることを確認を参照してください。
シミュレーション
"シミュレーション" は、モデルの "コンパイル" 後に、数値ソルバーを使用して指定の時間範囲に連続するタイム ステップでブロックのメソッドの出力と状態を計算するプロセスです。
各シミュレーション ループ時に、Simulink は Δt を計算して、タイム ステップ t(k+1) = t(k) + Δt を決定します。Δt のサイズはシミュレーションの解と実際の解の推定される誤差に基づきます。シミュレーションの終わりに、各タイム ステップの時間、状態、出力の結果のデータがベクトル [t, X, Y] として与えられます。

ソルバー
ソルバーは、モデルの方程式のセットに対する近似解を求めます。Simulink では、このタスクに確立された数値ソルバーが使用されます。
ソルバーのステップ サイズは固定または可変にすることができます。
固定ステップ –
Δtが定数のタイム ステップT(k+1) = T(k) + Δt。ステップ サイズが大きすぎる場合、シミュレーション結果には大きい誤差が生じる場合があります。次の例では、ステップ サイズ2で正弦波信号の形状を歪めています。固定ステップ ソルバーの場合はタイム ステップ サイズを指定し、可変ステップ ソルバーの場合はステップ サイズを自動決定することができます。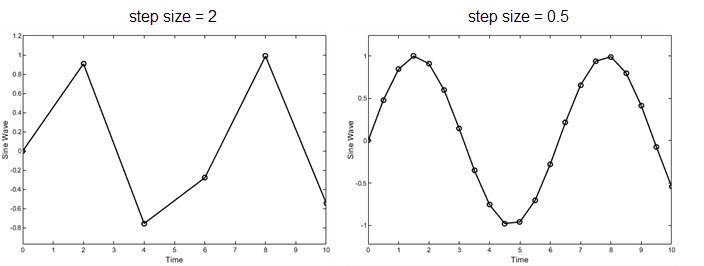
可変ステップ – 可変ステップ ソルバーは、許容誤差に基づいて解に到達するために反復します。タイム ステップは
T(k+1) = T(k) + Δtₖで、Δtₖは推定される誤差に応じてシミュレーション ステップごとに変化します。タイム ステップが小さいほど、シミュレーション結果の精度が向上します。計算の作業負荷を最小にするために、可変ステップ ソルバーは、許容誤差で指定された全体的なレベルの精度に達成し、ゼロクロッシングを確認して、最大ステップ サイズを選択します。これは、すべてのモデルの状態がユーザー指定の精度で計算されるようにします。
ソルバー メソッドはモデルの方程式の性質に応じて選択します。オイラー法は、y の接線の傾き (y') を使用して y の次の値を計算する単純な数値ソルバーです。y がランプ関数 x を積分する関数で傾きが 1 (y' = x) の場合、数値ソルバーは次の方程式を使用します。
x[n+1] = x[n] + Δt*1 y[n+1] = y[n] + Δt*x[n+1]
ステップ サイズを小さくすると結果の精度が向上しますが、シミュレーションが完了するまでの時間は長くなります。次の例では、ステップ サイズ 2 の方は 10 秒後に約 20 パーセントの誤差が見られますが、ステップ サイズ 0.5 の方は実際の解に近い結果になっています。
