Main Content

平面振子をモデル化する

モデルを開く

重力の影響の下で、長さ l の質量のない棒でつるされている質点 m について考えます。質量の位置は直交座標で (x,y) によって表すことができます。

システムのモデル化

質量の力平衡は、x 方向と y 方向の運動方程式を与えます。

$$
\begin{array}{rclccr}
m\ddot{x}&=&F\sin\theta&&(1)\\
m\ddot{y} + F\cos\theta&=&-mg&&(2)\\
\end{array}
$$

(u, v) をそれぞれ (x, y) の速度にします。システムは、1 次 ODE 系として書き換えることができます。

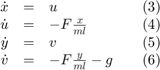
$$
\begin{array}{rclccr}
\dot{x} &=&u&&(3)\\
\dot{u}&=&-F\frac{x}{ml}&&(4)\\
\dot{y} &=&v&&(5)\\
\dot{v} &=&-F\frac{y}{ml} - g&&(6)
\end{array}
$$

ここで、F は棒の張力です。システムは、幾何制約も持ちます。

$$\begin{array}{rclccr}x^2 + y^2 &=& l^2&&(7)\end{array}$$

時間 t に関して (7) を 2 回微分して次を得ます。

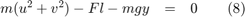
$$
\begin{array}{rclccr}
m(u^2 + v^2) -Fl-mgy&=&0&&(8)
\end{array}
$$

この関係は、システムの運動学をモデル化するために使用するステップごとに F を判断できるため、有用です。

システムのシミュレーション

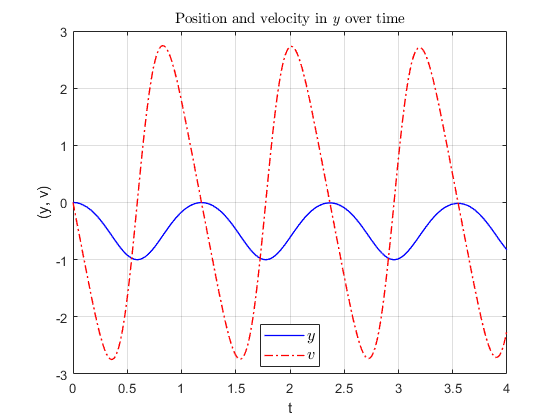
システムは、以下の図に示されるようにシミュレーションされます。

方程式 (8) には、1 つの不明な "F" があり、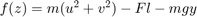$f(z) = m(u^2+v^2)-Fl-mgy$ とした場合、"f(z) = 0" の形式になります。Algebraic Constraint ブロックは、f(z) を 0 に制約し、(8) に合わせて F の解を求めます。

参考文献

Hairer, Ernst, Christian Lubich, and Michel Roche."The Numerical Solution Of Differential-Algebraic Systems By Runge-Kutta Methods."Lecture Notes in Mathematics.Vol. 1409, Berlin:Springer-Verlag, 1989: pp. 8-9.

参考