Algebraic Constraint
入力信号を制限
ライブラリ:
Simulink /
Math Operations
説明
Algebraic Constraint ブロックは、入力信号 f(z) を z または 0 に制限して、代数状態 z を出力します。このブロックは、入力で 0 または z を生成する値を出力します。出力は、直接フィードバック パスを通じて、入力に影響を与えなければなりません。すなわち、フィードバック パスには直達のあるブロックのみが含まれます。たとえば、インデックス 1 の微分代数方程式系 (DAE) の代数方程式を指定できます。
例
拡張例
端子
入力
出力
パラメーター
ブロックの特性
データ型 |
|
直達 |
|
多次元信号 |
|
可変サイズの信号 |
|
ゼロクロッシング検出 |
|
参照
[1] Garbow, B. S., K. E. Hillstrom, and J. J. Moré. User Guide for MINPACK-1. Argonne, IL: Argonne National Laboratory, 1980.
[2] Rabinowitz, P. H. Numerical Methods for Nonlinear Algebraic Equations. New York: Gordon and Breach, 1970.
[3] Kelley, C. T. Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics, Philadelphia, PA: 1995.
拡張機能
バージョン履歴
R2006a より前に導入

![$$ \left[\begin{array}{cc} 1 & 1\\ -1& 1 \end{array}\right]\left[\begin{array}{c}z_1\\z_2\end{array}\right] =\left[\begin{array}{c}1\\1\end{array}\right] $$](../../examples/simulink/win64/SolveALinearSystemOfAlgebraicEquationsExample_eq00627851823494940069.png)

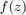
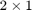
![$$\left[\begin{array}{c}z_1+z_2-1\\-z-1 + z_2-1\end{array}\right] $$](../../examples/simulink/win64/SolveALinearSystemOfAlgebraicEquationsExample_eq14029990663688292877.png)