システムのモデル化と検証

ステップ 3 - 2: Simulink によるモデルベース デザイン

• 1
• 2
• 3

ロボット システムの各コンポーネントをモデル化して、その物理的または機能的な動作を反映します。その後、モデルをテスト データでシミュレートして検証します。コンポーネントの Simulink^® モデルは、次のような複数のスタート地点に基づきます。

• 物理的コンポーネントの入力と出力の間にある明示的な数学的関係 — 代数的計算と微分方程式の積によって、直接的または間接的に、入力からコンポーネントの出力を計算できます。たとえば、与えられた流入速度から、タンクの水位を計算するのは、明示的な関係です。各 Simulink ブロックは、その入力から出力への計算の定義に基づいて実行されます。

• 物理的コンポーネントのモデル変数間の間にある暗黙的な数学的関係 — 変数は相互に依存しているため、コンポーネントに入力と出力を割り当てるのは単純ではありません。たとえば、ある回路のモーターのプラス (+) 端子の電圧とマイナス (-) 端子の電圧の間には、暗黙的な関係があります。Simulink でこのような関係にある変数をモデル化するには、Simscape™ などの物理的モデリング ツールを使用するか、入力/出力を定義可能な大きめのコンポーネントの一部としてモデル化します。場合によっては、モデリング目標とコンポーネント定義をじっくりと確認することが、入力/出力の関係を定義するのに役立ちます。

• 実際のシステムから得られたデータ — 実際のコンポーネントから入力/出力データを測定したが、完全に定義された数学的関係は存在していない場合です。多くのデバイスに、この説明に当てはまる、モデル化されていないコンポーネントが存在します。たとえば、テレビによって消費される熱です。System Identification Toolbox™ を使用すると、このようなシステムの入力/出力の関係を定義することができます。

• 明示的な機能的定義 — 機能的コンポーネントの出力を、入力をもとに代数演算や論理演算を使用して定義します。たとえば、サーモスタットの切り替えロジックです。ほとんどの機能的関係は、Simulink ブロックおよびサブシステムとしてモデル化できます。

このチュートリアルでは、明示的な入力/出力関係をもつ物理的コンポーネントおよび機能的コンポーネントをモデル化します。このチュートリアルでは、以下を行います。

1. システム方程式を使用して Simulink モデルを作成します。

2. Simulink エディターで Simulink ブロックを追加して接続します。ブロックは方程式の係数と変数を表します。

3. 各コンポーネントのモデルを個別に作成します。システムのモデルを最も効果的に作成する方法は、まず各コンポーネントを個別に考慮することです。

4. システムの近似を使用した簡単なモデルの作成から開始します。モデルの精度に影響を与える可能性がある仮定を特定します。複雑度のレベルがモデル化と精度の要件を満たすまで詳細を追加する作業を繰り返します。

5. 入力を指定して、出力を観察することで、コンポーネントを検証します。

システム レイアウトを開く

全システム レイアウトの全体像を把握することは、個々のコンポーネントをモデル化するときに役立ちます。このモデルは、個々のコンポーネントが相互にどのように関係するかを示しています。まず、system_layout モデルを読み込みます。

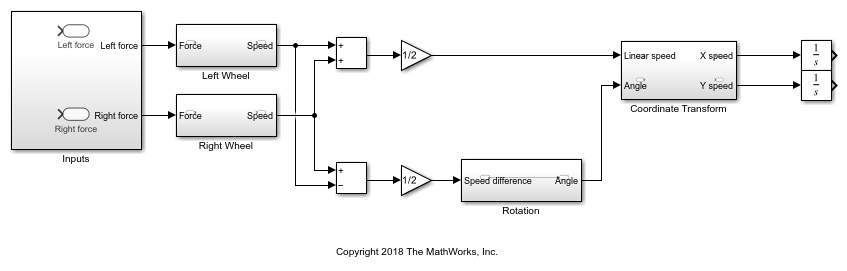
物理的コンポーネントのモデル化

たとえばデータ、エネルギー、力の伝達などのコンポーネント間の関係を記述します。Simulink でシステム方程式を使用して、ロボット システムのグラフィカル モデルを作成します。

コンポーネントをモデル化する前に次のような質問を検討します。

• 各コンポーネントのコンポーネントとは。変更しない限り変わらない値は何か。

• 各コンポーネントの変数とは。時間と共に変化する値は何か。

• コンポーネントがもつ状態変数の数は

科学的法則を利用して、各コンポーネントの方程式を導き出します。多くのシステム方程式は、次の 3 つのカテゴリに分けられます。

• 連続システムの場合、微分方程式は変数の変化率をすべての時間の値に対して定義された方程式を使用して記述します。たとえば、1 次微分方程式により、車の速度が得られます。

  $$\frac{dv(t)}{dt}=-\frac{b}{m}v(t)+u(t),$$

  ここで、

  • v(t) は時間 t の車の速度。

  • b は減衰係数。

  • m は車の質量。

  • u(t) は時間 t の車にかかる外力。

• 離散システムの場合、差分方程式は変数の変化率を記述しますが、方程式は特定の時間に対してのみ定義されます。たとえば、離散比例 - 微分コントローラーによる制御信号は次の方程式で記述されます。

  $$u[n]=K_{p}e[n]+\text{}{K}_d\frac{\left(e[n]-e[n-1]\right)}{T_s},$$

  ここで、

  • u[n] は離散時間ステップ n の制御信号。

  • e[n] は離散時間ステップ n の誤差。

  • e[n-1] は前の離散時間ステップ n-1 の誤差。

  • K_p は比例ゲイン。

  • K_d は微分ゲイン。

  • T_s はサンプル時間。

• 導関数を使用しない方程式は代数方程式です。たとえば、代数方程式によって、2 つのコンポーネントを使用した並列回路の全電流が次のように求められます。

  $$I_t=I_a+I_b,$$

  ここで、

  • I_t は回路を流れる全電流。

  • I_a は並列回路の分岐 a を流れる電流。

  • I_b は並列回路の分岐 b を流れる電流。

車輪の直線運動のモデル化

車輪には 2 つの力が働きます。

• モーターに働く力 — 力 F は、速度変更方向に沿って働く力で、その車輪のサブシステムの入力です。

• 抗力 — 力 F_drag は、速度変更方向と逆向きに働く力で、速度の関数です。

  $$F_{drag}=k_{drag}V\left|V\right|$$

加速度は、これらの力の合計に比例します。

$$\begin{array}{c}(m/2)\dot{V}=F-F_{drag}\\ (m/2)\dot{V}=F-k_{drag}V\left|V\right|\\ \dot{V}=\frac{F-k_{drag}V\left|V\right|}{(m/2)},\end{array}$$

ここで、k_drag は抵抗係数で、m はロボットの質量です。この質量の半分がそれぞれの車輪に乗っています。

車輪のモデルを作成するには、以下のようにします。

1. system_layout モデルで、Right Wheel という名前のサブシステムをダブルクリックし、空のサブシステムを表示します。

2. 速度と加速度をモデル化するために、Integrator ブロックを追加します。初期条件を 0 に設定したままにします。このブロックの入力は加速度 Vdot で、出力は速度 V です。

   

3. 抗力をモデル化するために、User-Defined Functions ライブラリから MATLAB Function ブロックを追加します。MATLAB Function ブロックは、数式をモデルに素早く実装できます。関数を編集するために、ブロックをダブルクリックして MATLAB Function ブロック エディターを開きます。

4. MATLAB Function ブロック エディターで、抗力を計算する MATLAB^® コードを入力します。

   function Fdrag=get_fdrag(V,k_drag)
   
   Fdrag=k_drag*V*abs(V);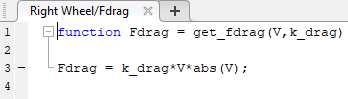

   

5. MATLAB Function ブロックの引数を定義します。MATLAB Function ブロック エディターで、[データの編集] をクリックします。k_drag をクリックし、[タイプ] を [パラメーター データ] に設定します。

6. Subtract ブロックを使用してモーター力から抗力を減算します。[ゲイン] パラメーターが 1/(m/2) に設定された Gain ブロックを使用して力 - 加速度の方程式を完成させます。

7. MATLAB Function ブロックの向きを反転させるため、ブロックを選択します。次に、Simulink ツールストリップの [書式設定] タブで、[左右を反転] をクリックします。ブロックを結線します。

   

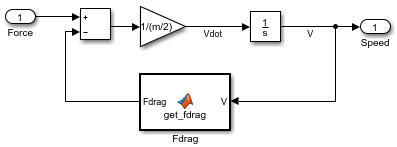
8. 2 つの車輪のダイナミクスは同じです。先ほど作成した Right Wheel という名前のサブシステムのコピーを作成し、それを Left Wheel という名前のサブシステムに貼り付けます。

親モデルを表示するには、[親に移動] をクリックします。

車輪の回転運動のモデル化

2 つの車輪がそれぞれ反対の方向に回転するとき、車輪は半径 r の円を描くように動き、ロボットの回転運動が起こります。両輪が同じ方向に回転するときは、回転は起こりません。車輪の速度の絶対値が常に同じであると仮定すると、2 つの車輪の速度 V_R と V_L の差に依存するものとして回転運動をモデル化できます。

$$\dot{\theta }=\frac{V_R-V_L}{2r}$$

回転ダイナミクスのモデルを作成するには、以下のようにします。

1. system_layout モデルの最上位で、Rotation という名前のサブシステムをダブルクリックし、空のサブシステムを表示します。Inport ブロックと Outport ブロック間の接続を削除します。

2. 角速度と位置をモデル化するために、Integrator ブロックを追加します。初期条件を 0 に設定したままにします。このブロックの出力は回転位置 $$\theta$$ で、入力は角速度 $$\dot{\theta }$$ です。

3. 接線速度から角速度を計算します。Gain ブロックを追加してブロックの [ゲイン] パラメーターを 1/(2*r) に設定します。

4. ブロックを結線します。

   

親モデルを表示するには、[親に移動] をクリックします。

機能的コンポーネントのモデル化

関数の入力から出力への関数を記述します。この記述には、代数方程式と論理構文を含めることができ、これらを使用して、Simulink でシステムのグラフィカル モデルを作成できます。

座標変換のモデル化

x 座標および y 座標におけるロボットの速度、V_X および V_Y は、直線運動速度 V_N および角度 $$\theta$$ と次のような関係にあります。

$$\begin{array}{l}{V}_X=V_N\cos \left(\theta \right)\\ V_Y=V_N\sin \left(\theta \right)\end{array}$$

座標変換のモデルを作成するには、以下のようにします。

1. system_layout モデルの最上位で、Coordinate Transform という名前のサブシステムをダブルクリックし、空のサブシステムを表示します。

2. 三角関数をモデル化するために、Math Operations ライブラリから SinCos ブロックを追加します。

3. 乗算をモデル化するために、Math Operations ライブラリから Product ブロックを 2 つ追加します。

4. ブロックを結線します。

   

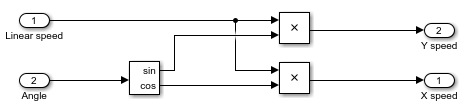
親モデルを表示するには、[親に移動] をクリックします。

モデル パラメーターの設定

以下のような複数のソースを使用して、モデル内のパラメーターの適切な値を決定できます。

• 標準のプロパティ テーブルや、メーカーのデータ シートなどの明文化された仕様書

• 既存システムの直接測定値

• システムの入力/出力を使用した推定値

system_layout モデルは、以下のパラメーターを使用します。

パラメーター	記号	値
質量	m	2.5 kg
転がり抵抗	k_drag	30 Ns2/m
ロボットの半径	r	0.15 m

Simulink モデルは、MATLAB ワークスペースで変数を使用して定義されたパラメーター値にアクセスできます。そうした変数を定義するには、MATLAB コマンド ウィンドウでコマンドを入力します。

m = 2.5;
k_drag = 30;
r = 0.15;

コンポーネントの検証

入力を指定して、出力を観察することで、コンポーネントを検証します。このようなシンプルな検証でも、モデルを改良するための即効性のある方法を指し示すことが可能です。この例では、次の動作を検証します。

• 車輪に力が継続的に加えられたとき、速度は定常状態の速度に達するまで上昇する。

• 2 つの車輪がそれぞれ反対の方向に回転するとき、回転角は一定の割合で増加します。

この例では、Outport ブロックを使用して、出力データのログをワークスペースとシミュレーション データ インスペクターに記録します。データのログ記録および他のログ記録手法の詳細については、シミュレーション データの保存を参照してください。

車輪のコンポーネントの検証

車輪のコンポーネントのテスト モデルを作成し、実行します。

1. 新しいモデルを作成します。[シミュレーション] タブで、[新規] をクリックします。Right Wheel という名前の Subsystem ブロックを新しいモデルにコピーします。

2. テスト入力を作成するために、Source ライブラリから Step ブロックを追加し、それを Right Wheel という名前のサブシステムの入力に接続します。[ステップ時間] パラメーターを 1 に設定したままにします。

3. 出力のログを記録するために、サブシステムを Outport ブロックに接続します。

   

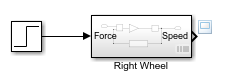
4. モデルのシミュレーションを実行します。[シミュレーション] タブで、[実行] をクリックします。

5. シミュレーション データ インスペクターで結果を確認するには、[データ インスペクター] をクリックします。データをプロットするには、Speed:1 信号の横のチェック ボックスをオンにします。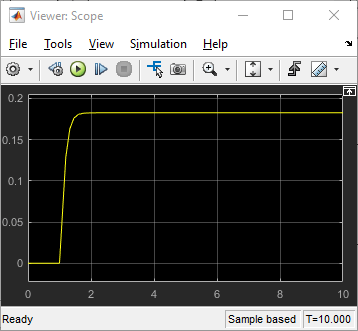

   

シミュレーション結果で、モデルが一般的に予想される動作を示していることが示されています。ステップ時間に力が加えられるまで、運動は行われていません。力が加えられると、速度が上昇しはじめ、加えられた力と抗力が平衡状態に達すると、一定の値で落ち着きます。検証に加えて、このシミュレーションでは、指定した力に対する車輪の最高速度も示されています。

回転のコンポーネントの検証

回転のコンポーネントのテスト モデルを作成し、実行します。

1. 新しいモデルを作成するために、[新規] をクリックします。Rotation という名前のサブシステム ブロックを新しいモデルにコピーします。

2. 新しいモデルでテスト入力を作成するために、Sources ライブラリから Step ブロックを追加します。[ステップ時間] パラメーターを 1 に設定したままにします。Step ブロックの出力を Rotation という名前のサブシステムの入力に接続します。この入力は、車輪が反対方向に回転するときの車輪速度の差を表します。

3. 出力のログを記録するために、サブシステムを Outport ブロックに接続します。

   

4. モデルのシミュレーションを実行します。[シミュレーション] タブで、[実行] をクリックします。

5. シミュレーション データ インスペクターで結果を確認するには、[データ インスペクター] をクリックします。データをプロットするには、Angle:1 信号の横のチェック ボックスをオンにします。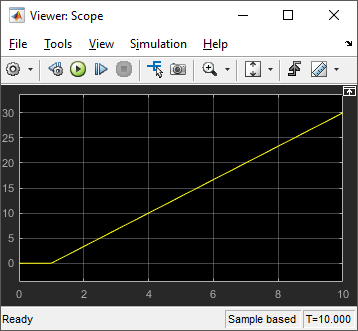

   

このシミュレーションは、各車輪が同じ速度で反対方向に回転しているとき、角度が一定の割合で増加することを示しています。モデルを改良して、角度の出力を解釈しやすくできます。たとえば、次のようなことができます。

• ゲインを 180/pi に設定した Gain ブロックを追加して、出力信号の単位をラジアンから度に変換する。

• 関数 mod をもつ Math Function ブロックを追加して、360 度のサイクルで出力値を表示する。

MATLAB 三角関数はラジアン単位で入力を受け取ります。

モデルの検証

各コンポーネントの検証を行った後、完成したモデルについて同様の検証を行うことができます。この例では、次の動作を検証します。

• 両輪に対して同じ方向に同じ力が加えられた場合、ロボットは直線移動をします。

• 両輪に対して反対方向に同じ力が加えられた場合、ロボットはその場で回転運動します。

車輪の同一方向の回転のテスト

両輪が同じ方向に回転しているときは、ロボットは直線移動をするはずです。

1. system_layout モデルで、Inputs という名前のサブシステムをダブルクリックし、空のサブシステムを表示します。

2. Step ブロックを追加して、テスト入力を作成します。[ステップ時間] パラメーターを 1 に設定したままにします。Step ブロックの出力を両方の Outport ブロックに接続します。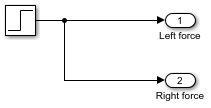

   

3. モデルの最上位で、両方の Integrator ブロックを Outport ブロックに接続してデータのログを記録します。信号に X position と Y position というラベルを付けます。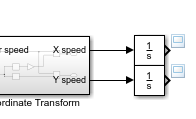

   

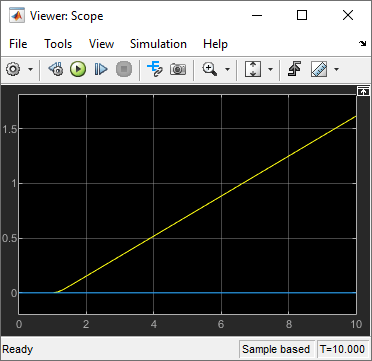
4. モデルのシミュレーションを実行します。

5. シミュレーション データ インスペクターで、X position 信号と Y position 信号を選択して結果を確認します。

角度は 0 で変化していないため、車両は想定どおり、x 方向にのみ移動します。

車輪の反対方向の回転のテスト

車輪が反対方向に回転しているときは、ロボットはその場で回転運動するはずです。

1. Inputs という名前のサブシステムをダブルクリックします。左車輪の方向を逆にするために、ソースと 2 番目の出力の間に Gain ブロックを追加して [ゲイン] パラメーターを -1 に設定します。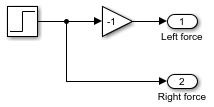

   

2. 角度の出力を信号ログ用にマークします。Rotation という名前のサブシステム ブロックからの出力信号を右クリックし、[選択した信号のログ] をクリックします。

3. モデルのシミュレーションを実行します。

4. シミュレーション データ インスペクターで、垂直方向に整列した 2 つのサブプロットを使用して信号を表示します。[可視化とレイアウト] をクリックします。次に、[基本レイアウト] で 2 行 1 列のレイアウトを選択します。上のサブプロットで、X position 信号と Y position 信号をプロットします。下のサブプロットで、Rotation:1 信号をプロットします。

上のサブプロットで、X-Y 平面に一切の運動が生じていないことが示されています。下のサブプロットで、定常の角運動が示されています。

この最終モデルを使用し、入力を変化させることで、さまざまなシナリオを調べることができます。

• 初期角度を 0 以外の値に設定するとどうなるかを観察する。

• 力が 0 になってから運動が停止するまでにどのくらいの時間がかかるかに注目する。

• ロボットの重量を増やす。ロボットがもっと重いときはどうなるかを観察する。

• 抵抗係数の低いもっと滑らかな表面をロボットが移動する場合はどうなるかを調べる。

参考

ブロック

• Pulse Generator | Gain | Integrator | Sum | Constant | Zero-Order Hold | Subsystem | MATLAB Function

ツール

• シミュレーション データ インスペクター | MATLAB Function ブロック エディター

参考

トピック

• Outport
• システムの定義とレイアウト
• Simulink におけるシステムの設計
• シミュレーション データの保存
• シミュレーション データ インスペクターを使用したプロットの作成

ステップ 3 - 2: Simulink によるモデルベース デザイン

• 1
• 2
• 3