Explore Techniques to Estimate Battery State of Charge
This example explores different techniques to estimate the state of charge (SOC) of a battery, including the Kalman filter algorithm and the Coulomb counting method. The Kalman filter is an estimation algorithm that infers the state of a linear dynamic system from incomplete and noisy measurements. This example illustrates the effectiveness of the Kalman filter in dynamically estimating the SOC of a battery, even when starting with inaccurate initial conditions and when the measurements are noisy. The SOC of a battery measures the current capacity of the battery in relation to its maximum capacity.
To highlight the accuracy of the Kalman filter, you also estimate the SOC of the battery by using the Coulomb counting algorithm. You then compare these results with the SOC values you previously estimated using the Kalman filter.
For a more straightforward and compact version of this example, see the Battery State-of-Charge Estimation example.
Measuring State of Charge in Electric Vehicles
Electric vehicles (EVs) provide a cleaner alternative to traditional combustion engine vehicles by using electricity as power source. This alternative power source allows the EVs to reduce the reliance on fossil fuels and cut down on greenhouse gas emissions and air pollution. EVs operate by using electric motors powered by batteries, which are the heart of any EV. These batteries determine the EV range, performance, and environmental footprint. However, managing the battery inside an EV is complex due to the inherent characteristics of the battery itself, including the battery energy density and weight, the thermal management, aging and degradation, and the estimation of the SOC and state of health (SOH).
The ability to track the SOC is crucial for managing battery systems efficiently and in applications where the battery performance and longevity are critical.
This figure shows a schematic of an electric vehicle (EV) that focuses on the battery management system (BMS) and its interaction with the battery, by highlighting how the BMS estimates the battery state of charge (SOC) using sensor data and the Kalman filter algorithm. The EV is equipped with temperature, current, and voltage sensors that tell you the values of these physical parameters at any given time. However, the EV lacks a dedicated SOC sensor because a direct SOC sensor as a single unit simply does not exist. To know the SOC value of your battery, you must estimate the SOC through algorithms that interpret the data from various sensors.

In this example, you estimate the SOC of a battery by using the Coulomb counting method and the Kalman filter algorithm:
Coulomb counting — Integrate current over time,
where is the nominal battery capacity, in ampere-hours (Ah), and is the battery current, in amperes.
Kalman filter — Predict the future state of charge of the battery and update this prediction based on new measurements.
State of Charge
The state of charge of a battery measures the charge level of the battery as a percentage of its total capacity. To calculate the SOC value as a percentage, you divide the charge of the battery by its total capacity, and multiply this value by 100:
where is the charge level of the battery, in Ah, and is the battery rated capacity, in Ah. Manufacturers provide the value of the rated capacity, which represents the maximum amount of charge in the battery. For example, if a battery has a capacity of 200 Ah and currently contains 100 Ah of charge, the SOC is equal to 50%.

The SOC is important for managing battery systems in many applications, including electric vehicles (EV) and renewable energy storage systems. If you know the SOC value of your battery, you can manage energy efficiently, prolong the life of the battery by preventing deep discharge cycles, and ensure system reliability.
Open Model
Open the model EstimateBatterySOCUsingKF. The model automatically loads the required parameters inside the BatterySOCEstimationData.m script by using a PreLoadFcn model callback.
This model represents a simplified Simscape™ implementation of the EV schematic in the previous section. The real initial SOC of the battery is 0.5 (or 50%), but the Kalman filter estimator starts with an initial condition that assumes the SOC to be 0.8 (or 80%). The battery undergoes a cycle of charging and discharging over a period of six hours. Despite the initial discrepancy between the actual SOC and the initial condition of the estimator, the Kalman filter quickly adjusts to accurately reflect the real SOC value. The estimation converges to the actual value in less than 10 minutes and then continues to accurately track the real SOC.
open_system('EstimateBatterySOCUsingKF')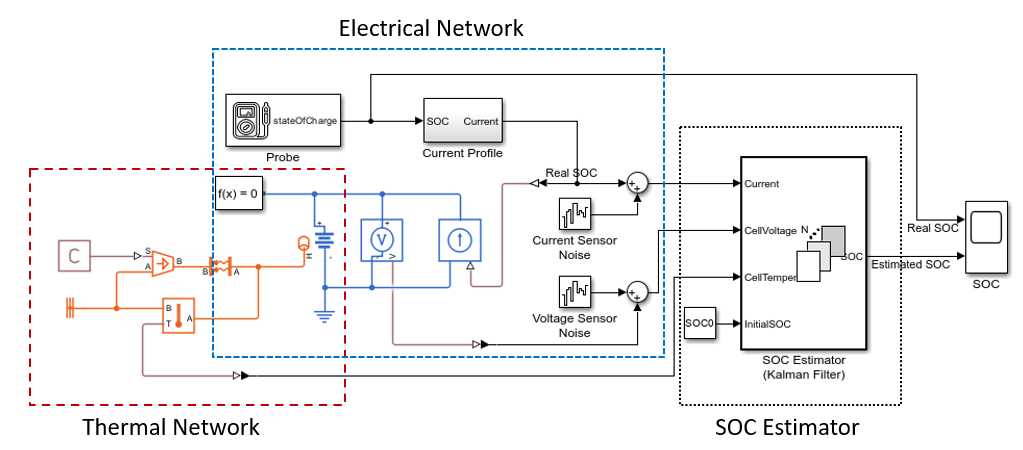
In this example, the extended Kalman filter is the algorithm that the SOC Estimator (Kalman Filter) block uses to estimate the battery SOC. To use a different Kalman filter implementation, in the SOC Estimator (Kalman Filter) block, set the Filter type parameter to Extended Kalman-Bucy Filter, Unscented Kalman Filter, or Unscented Kalman-Bucy Filter.
The model comprises three major components:
Thermal network — Model the heat exchange between a battery and its environment.
Electrical network — Model the battery and the current profile that charges and discharges the battery during the simulation.
SOC estimator — Estimate the SOC of the battery by using the Kalman filter algorithm.
Explore Thermal Network
The heat exchange between a battery and the environment affects the battery performance and its safety. Low or high temperatures reduce the performance of a battery, while excessive heat can lead to thermal runaway. In thermal runaway, the battery generates more heat than it dissipates, leading to fires or explosions.
This exchange happens through both conduction and convection. Conduction transfers the heat through materials. A battery generates heat due to the internal resistance and through electrochemical reactions during charging and discharge cycles. The materials of the battery then conduct this heat to its surface. Once the heat reaches the surface, the battery transfers this heat to the surrounding air or cooling fluid through convection. The efficiency of convective heat transfer depends on multiple factors, including the temperature difference between the battery surface and the environment, the surface area of the battery, and the velocity of the air or fluid. To learn more about the basics of conduction, convection, and thermal mass, see the Heat Conduction Through Iron Rod example.
This figures shows how this example models the thermal network of the battery:

To capture the thermal dynamics of the battery system, this model comprises:
Battery Equivalent Circuit block — Model the battery that generates and exchanges the heat.
Thermal mass of the battery — Represent the mass of the battery and its ability to store the heat. To model this mass, in the Battery Equivalent Circuit block, set the Thermal model parameter to
Lumped thermal massand, in the Thermal settings, specify a value for the Battery thermal mass parameter. This parameter represents the energy required to raise the temperature of the thermal port by one Kelvin.Convective Heat Transfer block — Model the heat exchange between the battery and the environment.
Controlled Temperature Source block — Represent an ideal energy source in a thermal network that maintains a controlled temperature difference regardless of the heat flow rate. This block models the ambient temperature. A and B are thermal conserving ports associated with the source inlet and outlet, respectively. Port S is a physical signal port that applies the control signal driving the source.
Temperature Sensor block — Measure the temperature of the battery. The SOC Estimator (Kalman Filter) block requires this temperature value.
The Convective Heat Transfer block represents the heat transfer by convection between the battery and the environment by means of fluid motion. The Newton law of cooling describes the transfer,
where:
is the heat flow, in watts (W).
is the convection heat transfer coefficient. In this example, this coefficient is equal to 5 W/(K*).
is the surface area. In this example, the surface area is the area of the battery cell and it is equal to 0.1019 .
and are the temperatures of the battery and the environment, in Kelvin.
A and B are thermal conserving ports associated with the points between which the heat transfer by convection takes place. Because the block positive direction is from port A to port B, the heat flow is positive if it flows from A to B.
Explore Electrical Network
This figure shows the elements that comprise the electrical network of the model:
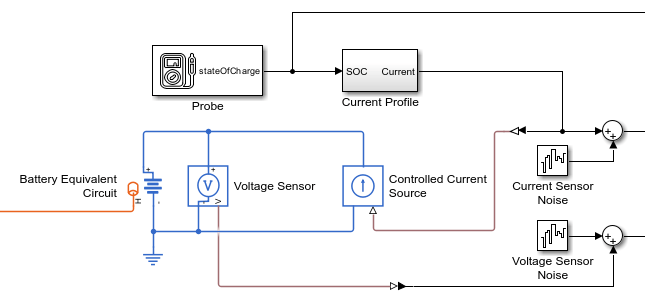
Battery Equivalent Circuit block — Model the battery of which you want to estimate the SOC.
Probe block — Output the SOC value of the battery as a Simulink® signal.
Controlled Current Source block — Represent an ideal current source that is powerful enough to maintain the current you specify through it regardless of the voltage across it. The output current is the numerical value at the physical signal input port, iT.
Current Profile subsystem — Model the profile of the current that you feed to the Controlled Current Source block through the input port, iT, which in turn generates the current flowing through the battery.
Sensor and noise — Measure the battery voltage that the SOC Estimator (Kalman Filter) block requires to estimate the SOC by using a Voltage Sensor block. The two Band-Limited White Noise blocks add noise to the current and voltage measurements to more accurately represent real-world applications.
Battery Equivalent Circuit Block
The Battery Equivalent Circuit block models the battery terminal voltage by using a combination of electrical circuit elements arranged in a specific circuit topology. This figure shows the equivalent circuit topology, which relies on variable resistances, variable capacitances, and a variable voltage source. Batteries do not respond instantaneously to load changes. They require some time to achieve a steady state. This time-varying property is a result of the battery charge dynamics. The block models the charge dynamics by using parallel RC sections in the equivalent circuit.

The Battery Equivalent Circuit calculates the terminal voltage of the battery at every time step by solving Kirchhoff's voltage law,
where:
is the open-circuit voltage.
is the instantaneous overpotential.
is the instantaneous resistance of the battery at the specified SOC and temperature values.
is the dynamic overpotential. This optional term depends on the number of parallel resistor-capacitor pairs. As the Battery Equivalent Circuit block in this example only models one time-constant dynamics, the dynamic overpotential only comprises one term.
is the voltage drop for parallel resistor-capacitor pair 1.
The software updates the battery state of charge SOC, the temperature T, and the corresponding variables that depend on them at every time step during the simulation. For the Battery Equivalent Circuit block, has a negative sign during discharge and a positive sign during charge. During discharge, the block subtracts the battery overpotentials from the open-circuit voltage value, lowering the terminal voltage of the battery. In the discharge and charge cases, the overpotentials dissipate energy as heat. This figure shows the evolution of the battery overpotentials during a battery pulse discharge. The dynamic overpotential from the resistor-capacitor pairs increases slowly over the pulse, as opposed to the instantaneous overpotential, which increases during the first few milliseconds.
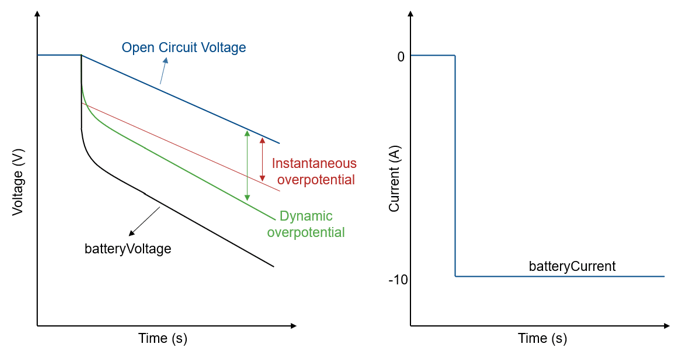
The battery in this example does not model self discharge, hysteresis, current directionality, battery fade, or calendar aging.
The block determines the battery temperature by summing all the ohmic losses in the battery,
,
where:
is the battery thermal mass.
corresponds to the ohmic loss contributor. Since this block models only one time-constant dynamics, these losses include the series resistance and the first charge dynamics segment.
is the voltage drop across the resistor .
is the resistor .
Battery Characterization
This example characterizes the battery by using the SOC, temperature, voltage, resistance, and cell capacity. The parameterization for the battery in this example corresponds to a lithium-ion battery. If you do not possess meaningful values for these parameters, or if you want to represent components by specific suppliers, you can parameterize the Battery Equivalent Circuit block with predefined parameterizations. These parameters match the manufacturer data sheets. To load a predefined parameterization, double-click the block, then click the <click to select> hyperlink of the Selected part parameter. The Block Parameterization Manager window opens and you can then choose the desired parameterization. For more information about pre-parameterization and for a list of the available components, see List of Pre-Parameterized Components (Simscape Electrical).
This figure shows the block parameters of the Battery Equivalent Circuit block.

Examine the vector of state of charge values, SOC_vec.
SOC_vec
SOC_vec = 1×7
0 0.1000 0.2500 0.5000 0.7500 0.9000 1.0000
The SOC_vec variable represents the vector of SOC breakpoints that define the points at which you specify the lookup data. This vector must be strictly ascending. The block calculates the SOC value with respect to the nominal battery capacity that you specify in the Cell capacity, AH parameter. This example characterizes the SOC of the battery with seven data points.
Examine the vector of temperatures, T_vec.
T_vec
T_vec = 1×3
278 293 313
The T_vec variable represents the vector of temperature breakpoints that define the points at which you specify lookup data. This vector must be strictly ascending and greater than 0 Kelvin. This example characterizes the battery temperature with three data points. These temperatures are in Kelvin.
Examine the open-circuit voltage, V0_mat.
V0_mat
V0_mat = 7×3
3.4900 3.5000 3.5100
3.5500 3.5700 3.5600
3.6200 3.6300 3.6400
3.7100 3.7100 3.7200
3.9100 3.9300 3.9400
4.0700 4.0800 4.0800
4.1900 4.1900 4.1900
The V0_mat variable represents the lookup data for the open-circuit voltages across the fundamental battery model at the SOC and temperature breakpoints you specified in the SOC_vec and T_vec variables. V0_mat is a 7-by-3 matrix. Each column relates to a temperature, and the rows relate to the SOC.
Examine the terminal resistance, R0_mat.
R0_mat
R0_mat = 7×3
0.0117 0.0085 0.0090
0.0110 0.0085 0.0090
0.0114 0.0087 0.0092
0.0107 0.0082 0.0088
0.0107 0.0083 0.0091
0.0113 0.0085 0.0089
0.0116 0.0085 0.0089
The R0_mat variable represents the lookup data for the series resistance of the battery at the SOC and temperature breakpoints you specified in the SOC_vec and T_vec variables. R0_mat is a 7-by-3 matrix. Each column relates to a temperature, and the rows relate to the SOC.
Examine the cell capacity, AH.
AH
AH = 27
The AH variable represents the capacity of the battery at full charge. The block calculates the SOC by dividing the accumulated charge by this value. The block calculates the accumulated charge by integrating the battery current.
In this example, these matrices are small, but you can characterize these table-based models to the level of granularity you require.
Current Profile
Open the Current Profile subsystem.
open_system("EstimateBatterySOCUsingKF/Current Profile")
The Current profile subsystem implements a simplified version of a system load by defining the current that flows through the battery. This current charges and discharges the battery during the simulation. During the charging process, the subsystem defines a current that charges the battery at a constant rate of 15 Amperes. During the discharging process, the subsystem introduces some variability with white noise and with uniform random numbers. By providing the discharge with some variability, you can better test the accuracy of the estimation.
The model feeds the current profile directly into a Controlled Current Source block to drive the battery.
Introduce Noise in Measurements for Kalman Filter
To evaluate the performance and robustness of the estimator, your simulation must represent real-world applications as closely as possible. In real-world applications, the data from sensors and measurements always contain noise due to sensor inaccuracies, environmental disturbances, or signal processing errors. A signal noise is the unwanted alteration in a signal that interferes with the accurate transmission of information. By introducing noise in the simulations, the model reflects the real operational conditions, making these simulations more reliable.
Theoretically, continuous white noise has a correlation time of 0, a flat power spectral density (PSD), and a total energy of infinity. In practice, white noise never disturbs physical systems, although white noise is a useful theoretical approximation when the noise disturbance has a correlation time that is very small relative to the natural bandwidth of the system. In Simulink, you can simulate the effect of white noise by using a random sequence with a correlation time much smaller than the shortest time constant of the system. This example introduces noise to the current and voltage measurements by using two Band-Limited White Noise blocks. The correlation time of the noise is the sample rate of the blocks. For accurate simulations, use a correlation time much smaller than the fastest dynamics of the system. You can get good results by specifying:
where is the bandwidth of the system in rad/sec.
The SOC Estimator (Kalman Filter) block receives the noisy current and voltage measurements. Then the block estimates the battery SOC against such uncertainties and disturbances. By adding noise, you can effectively assess how well the filter extracts the signal from the noise, which is essential for applications where the precision is critical.
Noisy measurements are also useful for tuning the parameters of the filter. The effectiveness of the Kalman filter depends on the correctness of its parameters, including the process noise covariance and the measurement noise covariance matrices.
Kalman Filter for State of Charge Estimation
From a practical perspective, the direct measurement of the SOC of a battery is not straightforward because the SOC is not a directly observable quantity such as the voltage or the current. The SOC is a derived parameter and reflects the internal chemical state of the battery. This chemical state varies with multiple factors including age, temperature, and discharge rate. Since direct measurement is challenging, you must estimate the SOC value.
This example uses the Kalman filter algorithm to estimate the battery SOC. The Kalman filter algorithm estimates the state of a linear dynamic system from noisy measurements. To estimate the SOC of a battery, the Kalman filter predicts the future state and then updates this prediction based on the new measurements. The Kalman filter provides accurate estimates even with noisy data, adapts to behavioral changes in the battery, including aging effects, and incorporates different measurements to improve the SOC estimation, such as voltage, current, and temperature. To learn more about Kalman filters, see the Understanding Kalman Filters introductory examples.
The SOC Estimator (Kalman Filter) block provides four different Kalman filter algorithms for SOC estimation. This example focuses on the extended Kalman filter (EKF) algorithm.
This figure show the equivalent circuit for a battery with one-time-constant dynamics:
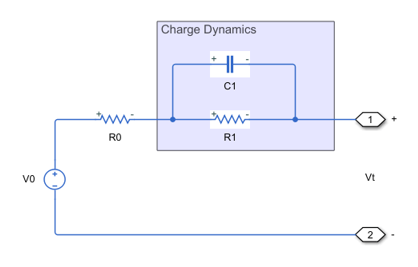
The equations for the equivalent circuit with one time-constant dynamics are:
In these equations:
is the state of charge.
is the current.
is the no-load voltage.
is the terminal voltage.
is the ampere-hour rating.
is the polarization resistance.
is the parallel RC capacitance.
is the temperature.
is the polarization voltage over the RC network.
A time constant for the parallel section relates the polarization resistance and the parallel RC capacitance using the relationship .
For the Kalman filter algorithms, the block uses this state and these process and observation functions:
This diagram shows the internal structure of the extended Kalman filter (EKF) in the SOC Estimator (Kalman Filter) block:

The EKF technique relies on a linearization at every time step to approximate the nonlinear system. To linearize the system at every time step, the algorithm computes these Jacobians:
The EKF is a discrete-time algorithm. After the discretization, the Jacobians for the SOC estimation of the battery are:
where is the sample time and is the open-circuit voltage.
The EKF algorithm comprises three phases: initialization, prediction, and correction.
Initialization
The EKF algorithm initializes the state estimate and the uncertainty (covariance) of this state at 0 seconds.
— State estimate at time step 0 using measurements at time step 0.
— State estimation error covariance matrix at time step 0 using measurements at time step 0.
is the covariance of the initial error. is a square matrix that represents the uncertainty in the initial estimates of the state of the system and contains the covariances between all pairs of the initial estimates of the state. The diagonal elements represent the uncertainties in each variable of the state. The off-diagonal elements represent the covariances between the different variables of the state. This matrix depends on the knowledge of the initial state, desired convergence speed, and stability of the filter. If you have a good initial estimate of the state, you can set this matrix to a small value. If the initial value is uncertain, set this matrix to higher values. The choice of the matrix is important as it affects the performance of the filter, especially at the beginning of the simulation. If you set too low, you are representing an overconfidence in the initial estimates and the filter might be too slow to adjust to the actual behavior of the system. If you set too high, you are representing almost no confidence in the initial estimates and the filter might rely too much on the first few measurements. This action might destabilize the estimation of the state if the measurements are noisy or inaccurate.
Prediction
The EKF algorithm predicts the future SOC based on the behavior of the battery, such how it discharges or charges under certain conditions, and the control inputs, for example if the battery is drawing or supplying current. This prediction results in a predicted state and a predicted error in the estimate. The prediction state moves the state estimate forward in time.
Project the states ahead (a priori):
Project the error covariance ahead:
where is the covariance of the process noise.
The covariance of the process noise, , is a square matrix that represents the uncertainty in the state transition model and contains the covariances between all pairs of the components of the process noise. The diagonal elements represent the uncertainties of each component in the process noise. The off-diagonal elements represent the covariances between the different components in the process noise. You often determine it through a combination of system identification, experiments, and domain knowledge. Higher values of the elements in the matrix indicate greater uncertainty and unpredictability in the dynamics of the system.
Correction
The EKF algorithm uses the information from new measurements to update the predictions of the state and error. The filter calculates the measurement residual, which is the difference between the actual measurements and the predictions. This difference represents the inaccuracy in the prediction. The filter then updates the predicted state based on the measurement residual. This process involves calculating the Kalman gain that determines how much the filter must correct the predictions based on the new measurements. To calculate the Kalman gain, the algorithm uses the covariance of the measurement noise, .
The covariance of the measurement noise, , is a square matrix that represents the uncertainty in the observation model and contains the covariances between all pairs of measurement errors. The diagonal elements represent the uncertainties in each measurement. The off-diagonal elements represent the covariances between different measurements, that indicate how much the noise in one measurement correlates with the noise in another measurement. Higher values of the elements in the matrix indicate higher measurement noise or less confidence in the sensor. This matrix depends on the characteristics of the sensors and on their accuracy. For example, if the standard deviation of the sensor is equal to 0.01, then a good value for is .
Compute the Kalman gain:
Update the estimate with the measurement (a posteriori):
Update the error covariance:
This process repeats for each new measurement and the Kalman filter continuously improves the state estimate by balancing the predictions of the model with the real-world measurements.
Plot Real and Estimated State of Charge
Simulate the model.
sim("EstimateBatterySOCUsingKF.slx");Create a figure to plot the real and estimated SOC values.
FigureEstimateBatterySOCUsingKF = figure(Name="EstimateBatterySOCUsingKF");
figure(FigureEstimateBatterySOCUsingKF)
clf(FigureEstimateBatterySOCUsingKF)Get the simulation time, real SOC, and estimated SOC values from the simulation output.
time = SimulationOutputKalmanFilter.time/3600; SOCRealKF = SimulationOutputKalmanFilter.signals(1).values(:)*100; SOCEstKF = SimulationOutputKalmanFilter.signals(2).values(:)*100;
Plot the real and estimated SOC values.
plot(time,SOCRealKF,LineWidth=1,Color="blue") hold on plot(time,SOCEstKF,LineWidth=1,Color="red") hold off grid on title('Real and Estimated State of Charge') ylabel('SOC (%)') xlabel('Time (hours)') legend({'Real','Estimated'},Location="Best");
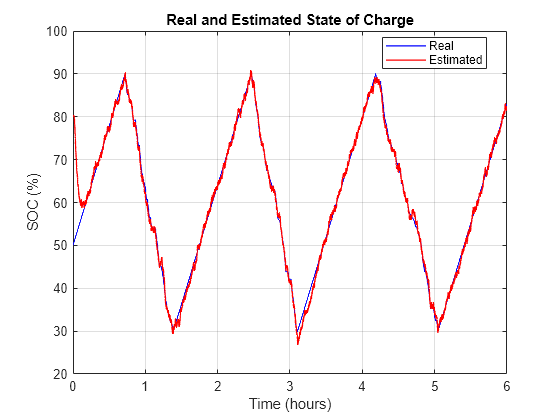
The initial SOC of the battery is equal to 0.5. The estimator uses an initial condition for the SOC equal to 0.8. The extended Kalman filter estimator converges to the real value of the SOC in less than 10 minutes and then follows the real SOC value.
Compare Kalman Filter Estimation with Coulomb Counting Estimation
To highlight the accuracy of the Kalman filter algorithm, estimate the SOC of the same battery model by using the Coulomb counting method. The Coulomb counting method estimates the SOC of the battery by integrating the current that flows through the battery over time. This section shows you how the Coulomb counting estimator fails to converge to the real value of the SOC if the initial estimate is wrong.
Open Coulomb Counting Model
Open the model EstimateBatterySOCUsingCC. The real initial SOC of the battery is 0.5 (or 50%), but the Coulomb counting estimator starts with an initial condition that assumes the SOC to be 0.8 (or 80%). The battery undergoes a cycle of charging and discharging over a period of six hours.
open_system('EstimateBatterySOCUsingCC')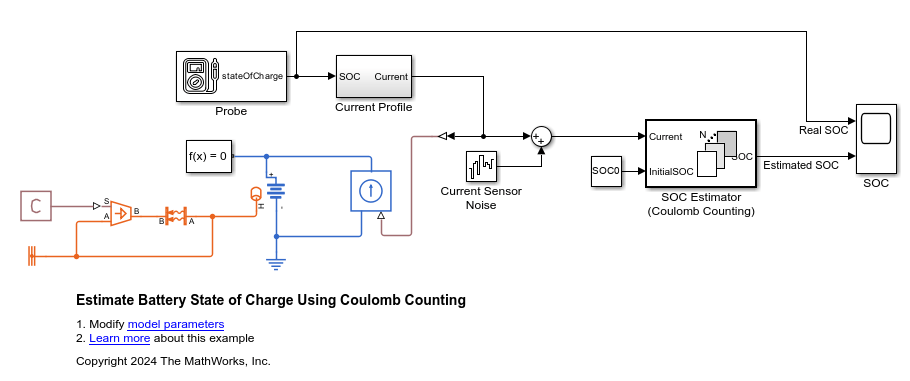
The thermal and electrical network of this model are identical to those of the EstimateBatterySOCUsingKF model.
This diagram shows the structure of the SOC Estimator (Coulomb Counting) block:

To compute the SOC of the battery, the SOC Estimator (Coulomb Counting) block counts the Ampere hour and current integration.
Compare Estimated State of Charge with Coulomb Counting and Kalman Filter
Simulate the EstimateBatterySOCUsingCC model.
sim("EstimateBatterySOCUsingCC.slx");Create a figure to plot the real and estimated SOC values.
FigureEstimateBatterySOCUsingCC = figure(Name="EstimateBatterySOCUsingCC");
figure(FigureEstimateBatterySOCUsingCC)
clf(FigureEstimateBatterySOCUsingCC)Get the simulation time, real SOC, and estimated SOC values from the simulation output.
time = SimulationOutputCoulombCounting.time/3600; SOCRealCC = SimulationOutputCoulombCounting.signals(1).values(:)*100; SOCEstCC = SimulationOutputCoulombCounting.signals(2).values(:)*100;
Plot the real SOC values and the SOC values that you estimated using both the Kalman filter and the Coulomb counting algorithms.
plot(time,SOCRealCC,LineWidth=1,Color="blue") hold on plot(time,SOCEstCC,LineWidth=1,Color="magenta") plot(time,SOCEstKF,LineWidth=1,Color="red") hold off grid on title('Real and Estimated SOC with Coulomb Counting and Kalman Filter') ylabel('SOC (%)') xlabel('Time (hours)') legend({'Real','Estimated Coulomb Counting','Estimated Kalman Filter'},Location="Best");
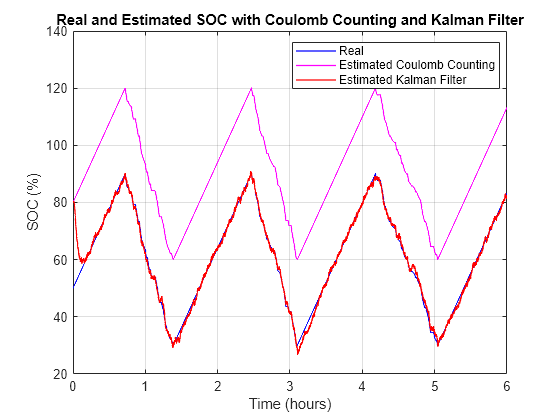
The initial SOC of the battery is equal to 0.5. The estimator uses an initial condition for the SOC equal to 0.8. The Coulomb counting estimator fails to converge to the real value of the SOC due to the error in the initial estimation. However, if you initialize the Coulomb counter correctly, and if you know the capacity of the battery with absolute certainty, the Coulomb counting method actually outperforms the Kalman filter in accuracy for a specific load case of short duration. The main problem with the Coulomb counting method arises over longer periods of time, as the estimated battery SOC slightly starts to drift away from the actual real value due to the self-discharge behavior of the battery. All batteries experience this self-discharge behavior during storage conditions due to the internal chemical reactions or other processes that consume charge from the battery. When the battery is off, the battery management system (BMS) does not wake up often enough to accurately recalculate the SOC. For example, if you leave an electric vehicle (EV) battery pack uncharged and in storage for a couple of weeks, a lithium-ion battery pack can lose around 2% of its SOC. The BMS cannot detect this loss and it is not accounted for in the Coulomb counter. This self-discharge rate also changes over the lifetime of a battery. As such, with Coulomb counting, every time the BMS wakes up after a long period of time (for example, after just hours or even a two-week storage period), it perceives its SOC to be different from its actual value and lacks the capability to correct this discrepancy in the initial value. Over time, this difference significantly accumulates.
For these reasons, choosing the correct algorithm to estimate the SOC value of your battery depends on multiple factors, including the model dependency, computational complexity, accuracy, and adaptability. In general, the Kalman filter offers higher accuracy and adaptability (if you properly set the , , and matrices), but requires more detailed system models and is also more complex to implement and computationally more intensive. The Coulomb counting algorithm, instead, is easier to implement and does not require a model of the system, but it is also less adaptable to changes in the battery characteristics.
References
[1] Plett, Gregory L. Battery Management Systems. Volume I, Battery Modeling. Artech House, 2015.
[2] Plett, Gregory L. Battery Management Systems. Volume II, Equivalent-Circuit Methods. Artech House, 2015.
[3] Kalman, R. E. 'A New Approach to Linear Filtering and Prediction Problems'. Journal of Basic Engineering, vol. 82, no. 1, Mar. 1960, pp. 35–45. DOI.org (Crossref), https://doi.org/10.1115/1.3662552.
See Also
SOC Estimator (Kalman Filter) | SOC Estimator (Coulomb Counting)