鉄のロッドを通じた熱伝導

ライブスクリプトを開く

この例では、一方の端が高温ベースに固定されており、その長さに沿った部分と自由端が空気にさらされている長い鉄のロッドを熱ブロックでモデル化する方法を示します。このロッドは、その長さに沿って伝導が行われ、その長さに対して垂直方向に空気との対流が行われる拡大面です。拡大面は、固体を冷却するためのフィンとしてよく使われます。

このシナリオでは、ベースは壁面に固定されており、その温度は摂氏 100 度です。熱は伝導を介してロッドを伝わり、ロッドの熱質量を徐々に加熱します。熱は、温度が摂氏 20 度の周囲空気との自然対流を介してロッドの円柱面と自由端から放出されます。初期状態では、ロッド全体の温度は周囲の気温と同じです。ロッドを伝わる温度は約 1500 秒後に定常状態に達します。このロッドは鉄製で、長さ 20 cm、直径 2.5 cm です。

この例では、最初に、エネルギー保存の法則、伝導と対流の熱伝達メカニズム、熱質量の特性という、ロッドの基本的な熱効果について説明します。次に、この例では、熱効果を組み合わせてロッドの完全な熱モデルを 2 つ考えます。1 つ目の熱モデルには単一の集中質量が含まれ、2 つ目は複数の集中質量が含まれる有限差分モデルです。この例では、ロッドに関する 2 つの異なる熱モデルの計算コストと忠実度のトレードオフについて考えます。この例では、モデルが定常状態の解析解でどの程度適切に収束するかを比較します。

% Model parameters

% Thermal conditions
T_air     = 20;        % Air temperature           [degC]
T_base    = 100;       % Base temperature          [degC]
T_init    = T_air;     % Initial rod temperature   [degC]

% Geometric parameters
L         = 0.2;       % Rod length                [m]
D         = 0.025;     % Rod diameter              [m]
A         = pi*D^2/4;  % Rod cross-sectional area  [m^2]
A_cyl     = pi* D * L; % Rod cylindrical surface area [m^2]

% Iron material properties
rho       = 7800;      % Iron density              [Kg/m^3]
k         = 80.2;      % Iron thermal conductivity [W/(K*m)]
h         = 32.1;      % Convective heat transfer coefficient [W/(m^2*K)]
c         = 447;       % Iron specific heat [J/kg/K]

m         = rho*A*L;   % Rod mass [kg]

エネルギー保存の法則

熱力学第一法則は、孤立系のエネルギー総量は常に一定に保たれるという、物理学の基本原則です。この法則は、仕事率の観点から数学的に次のように表されます。

$\frac{d U}{d t} = Q - W$ .

パラメーターは次のとおりです。

$\frac{dU}{dt}$ は時間に対する内部エネルギーの変化率です (SI 単位の "W" で測定)。
$Q$ は系に加えられた熱の比率です ("W" で測定)。
$W$ は系がした仕事の比率です ("W" で測定)。

仕事が発生しない熱系では、内部エネルギーの変化率は系に加えられた熱の増加率と等しくなります。

$\frac{d U}{d t} = Q$ .

鉄のロッドでは、伝導と対流の熱伝達 ( $Q$ ) により、ロッドの熱質量に蓄積された内部エネルギー ( $U$ ) が変化します。

伝導

熱伝導は、材料を通じた熱伝達のプロセスです。材料が加熱されると、その分子が運動エネルギーを得るため、運動が増加します。このように運動が高まることで、隣接する分子との衝突が発生し、プロセスにおいてエネルギーが伝達されます。この伝達は、熱平衡に達して物質全体で温度が均一になるまで続きます。

熱伝導方程式はフーリエの法則とも呼ばれ、材料を通じた熱伝達率を表します。

$Q = k \frac{A}{L} (T_{1} - T_{2})$ ,

ここで、

$Q$ は端 $1$ から端 $2$ への熱流量です ("J" で測定)。
$k$ は材料の熱伝導率です ("W/(K m)" で測定)。
$S$ は熱流量の方向に対して法線方向の面積です ("m^2" で測定)。
$L$ は熱流量の方向の厚さです ("m" で測定)。
$T_{1}$ と $T_{2}$ は伝導伝熱素子のどちらかの端の温度です ("degC" で測定)。

例 1 - 定常状態の伝導

ロッドに関する次の簡単なシナリオについて考えます。このロッドは、その長さに沿って空気との対流熱伝達が発生しないように断熱されています。一定の 18 W の熱がロッドを流れてロッドの先端から放出されます。ロッドの先端の温度は何度でしょうか。

熱伝導方程式を並べ替えると、ロッドの先端の温度は次のようになると想定されます。

$T_{E n d} = T_{B a s e} - \frac{L}{A k} Q$

% Example parameter
Q_case_1  = 18;       % Heat flow rate through rod [W]

% Expected rod tip temperature
T_rod_tip_steady_case_1 = T_base - L/(A*k)*Q_case_1 % [degC]

T_rod_tip_steady_case_1 = 8.5554

モデル HeatConductionThroughInsulatedIronRod を開いて解析解を検証します。熱モデルは、ベースの温度に設定された Temperature Source、Conductive Heat Transfer 素子、および 18 W に設定された Heat Flow Rate Source で構成されています。

mdl = 'HeatConductionThroughInsulatedIronRod';
open_system(mdl);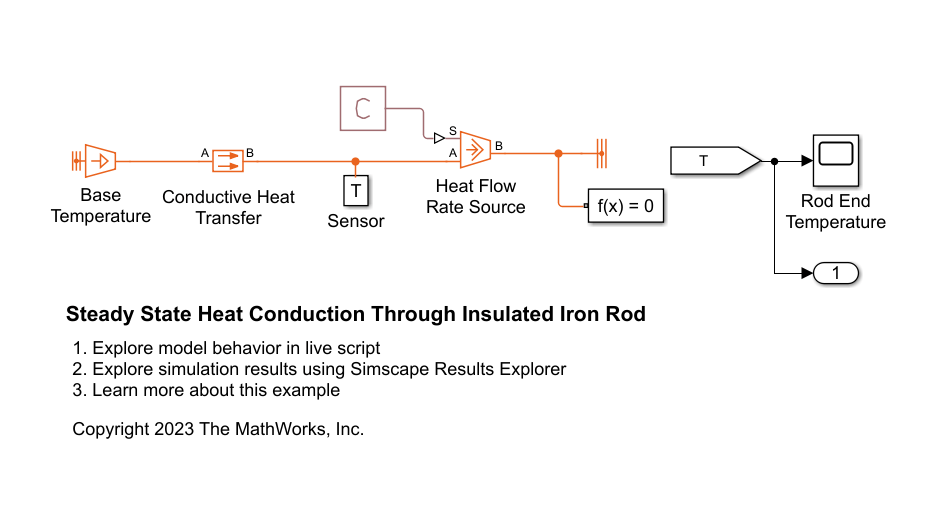

モデルをシミュレートし、シミュレーション結果を解析解と比較します。

sim(mdl);
% Get the simulation output
T = yout; % [degC]

% Display the temperature 
T_rod_tip_simulated_case_1 = T(end) % [degC]

T_rod_tip_simulated_case_1 = 8.5554

シミュレーション結果は解析解と一致しています。

対流

対流は、流体の移動を通じた熱伝達のプロセスです。流体の移動と伝導が組み合わさることで、流体内の温度の高い領域から低い領域へ熱エネルギーが運ばれます。温度勾配に起因する密度の差により、流体内で自然対流が発生します。流体は、加熱されると密度が低くなって上昇する傾向があり、より低温で密度の高い流体が流れ込んでそれに置き換わります。これにより、流体内で温度の高い領域から低い領域へ熱が運ばれる循環パターンが確立されます。

熱対流方程式はニュートンの冷却の法則と呼ばれ、表面から周囲の流体への熱伝達率を表します。

$Q = h A_{C o n v} (T_{1} - T_{2})$ ,

ここで、

$h$ は対流熱伝達係数です ("W/(K m^2)" で測定)。
$A_{Conv}$ は表面積です ("m^2" で測定)。
$T_{1}$ と $T_{2}$ はそれぞれ表面と周囲の流体の温度です ("degC" で測定)。

例 2 - 定常状態の対流

ロッドに関する別の簡単なシナリオについて考えます。ロッド全体の温度は摂氏 250 度に維持されています。周囲温度は摂氏 20 度で、ロッドと空気の間の対流熱伝達係数は 32.1 W/(m^2 K) です。ロッドの円柱面と空気の間の熱伝達率はどれくらいでしょうか。

熱対流方程式にモデルパラメーターを代入して熱伝達率を計算します。

% Example parameter
T_cyl_uniform_case_2 = 55;       % Rod uniform temperature [degC]

% Expected rate of convective heat transfer
Q_conv_case_2 = h * A_cyl * (T_cyl_uniform_case_2 - T_air) % [W]

Q_conv_case_2 = 17.6479

モデル HeatConvectionFromIronRod を使用して解析解を検証します。熱モデルは、ロッドの温度に設定された Temperature Source、周囲温度に設定された Temperature Source、その間にある Convective Heat Transfer 素子で構成されています。

mdl = 'HeatConvectionFromIronRod';
open_system(mdl);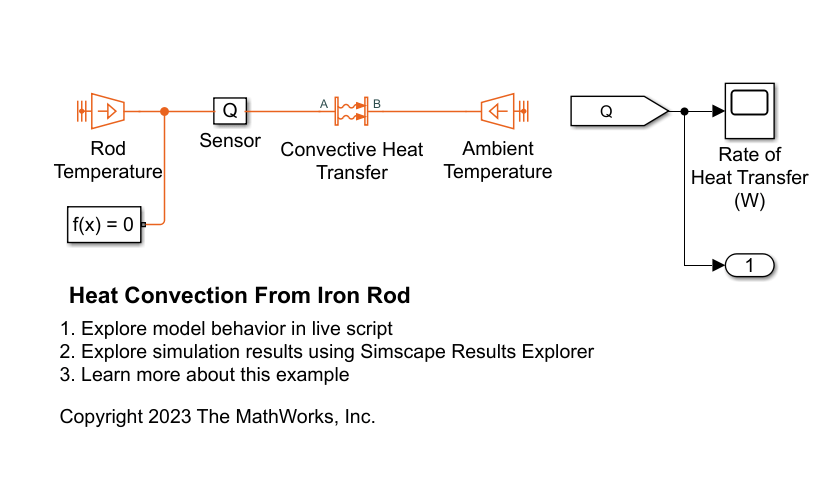

モデルをシミュレートし、シミュレーション結果を解析解と比較します。

sim(mdl);

% Get the simulation output
Q = yout; % [W]

% Display the rate of heat transfer
Q_conv_simulated_case_2 = Q(end) % [W]

Q_conv_simulated_case_2 = 17.6479

シミュレーション結果は解析解と一致しています。

熱質量

熱質量は、材料が熱エネルギーを蓄積し解放する能力を示します。熱質量の内部エネルギーの変化は、次の方程式で表されます。

$\frac{d U}{d t} = c m \frac{d T}{d t}$ ,

ここで、

$\frac{dU}{dt}$ は時間に対する内部エネルギーの変化率です ("W" で測定)。
$c$ は材料の比熱です ("J/(Kg K)" で測定)。
$m$ は質量です ("kg" で測定)。
$T$ は温度です ("degC" または "K" で測定)。

材料の内部エネルギー $U$ の変化率は、その温度 $T$ の変化率に比例します。比熱容量 $c$ は、材料の単位質量の温度を 1 度変化させるのに必要なエネルギー量を表します。熱質量 $cm$ が大きいと、系の温度変化の速度が低下します。

例 3 - 熱質量における過渡温度応答

ロッドの簡単なシナリオについて考えます。このシナリオでは、完全に断熱されたロッドに 18 W の熱が流入します。単純化のため、ロッド全体の温度が均一に上昇すると仮定します。ロッドの温度の上昇率はどれくらいになるでしょうか。

熱力学第一法則を使用すると、断熱されたロッドに流入する熱は、ロッドの内部エネルギーの変化に等しくなります。

$Q = c m \frac{d T}{d t}$ .

方程式を並べ替えて温度変化率の解を求めます。

% Example parameter
Q_case_3  = 18;       % Heat flow rate through rod [W]
% Expected rate of temperature change
dT_dt_case_3 = Q_case_3 / (c*m) % Rate of temperature change [degC/sec]

dT_dt_case_3 = 0.0526

モデル ThermalMassIronRod を使用して解析解を検証します。

mdl = 'ThermalMassIronRod';
open_system(mdl);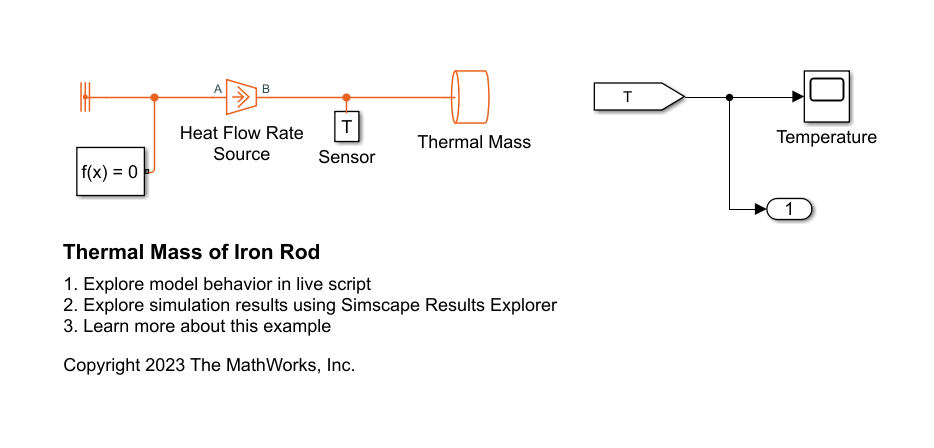

モデルをシミュレートし、シミュレーション結果が解析解と一致することを確認します。

sim(mdl);

% Get the simulation output
T = yout; % [degC]
t = tout; % [sec]

% Calculate rate of temperature change
dT = T(end) - T(1);
dt = t(end) - t(1);
dT_dt_simulated_case_3 = dT / dt % [degC/sec]

dT_dt_simulated_case_3 = 0.0526

シミュレーション結果は解析解と一致しています。

過渡的な熱挙動をもつロッド

伝導、対流、熱質量の各要素を組み合わせて過渡的挙動をもつロッドを完全にモデル化します。ロッドのベースの温度は摂氏 100 度です。このロッドでは、その長さに沿って伝導が行われ、その長さに沿った部分と先端で空気との自然熱対流が行われます。初期状態では、ロッドの温度は周囲の気温、摂氏 20 度と同じです。

集中質量 Rod モデル

ロッドの過渡的な熱挙動を取得するための単純なモデルには、単一の熱質量が含まれます。モデル HeatConductionTroughIronRodLumped を開きます。

lumped_mass_model = 'HeatConductionThroughIronRodLumped';
open_system(lumped_mass_model)

Rod サブシステムを開きます。

open_system([lumped_mass_model '/Rod'])

Rod モデルで、2 等分された Conductive Heat Transfer 素子間の中間ノードはロッドの中間点を表します。中間ノードにおける単一の熱質量は、ロッドの質量全体を中間点温度の維持としてモデル化します。Convective Heat Transfer 素子は、ロッドの円柱面とロッドの端点から周囲の大気への対流をモデル化します。

熱力学第一法則を使用すると、熱質量の内部エネルギーの変化率は、中間ノードを通る正味熱流量に等しくなります。

$\frac{d U}{d t} = Q$ .

ノードへの正味熱流量は、ベースからの伝導、円柱面に沿った空気との対流、およびロッドの先端での伝導と対流に起因します。

$Q = Q_{L e f t} + Q_{C y l} + Q_{R i g h t}$ .

中間ノードの左側では、ベースからの伝導によりノードに熱が流入します。

$Q_{L e f t} = k \frac{2 A}{L} (T_{B a s e} - T)$ ,

ここで、 $T$ は中間ノードの温度です。

ロッドの円柱面に沿って、空気との対流によりノードから熱が流出します。

$Q_{C y l} = h A_{C y l} (T_{A i r} - T)$ .

中間ノードの右側では、ロッド内の伝導に続いてロッドの先端と空気の間の対流により熱が流出します。

$Q_{R i g h t} = k \frac{2 A}{L} (T_{E n d} - T)$ ,

$Q_{R i g h t} = h A (T_{A i r} - T_{E n d})$ ,

ここで、 $T_{End}$ はロッドの先端の温度であり、ロッドの先端は Simscape™ モデル内の "Conduction1B" の B 端子と "Convection End" の A 端子のジャンクションに対応します。 $Q_{Right}$ 方程式を並べ替えて $T_{End}$ を除外します。

$Q_{R i g h t} = \frac{2 A k h (T_{A i r} - T)}{L h + 2 k}$ .

熱流量の式と熱質量の内部エネルギー変化の式をエネルギー保存の方程式に代入すると、ロッドの温度 $T$ の支配微分方程式になります。

$c m \frac{d T}{d t} = k \frac{2 A}{L} (T_{B a s e} - T) + h A_{C y l} (T_{A i r} - T) + \frac{2 A k h (T_{A i r} - T)}{L h + 2 k}$ .

Simscape ネットワークはノードにおける熱伝達を合計しますが、これはこの微分方程式と等価です。

Segmented Rod モデル

ロッドの過渡的な熱挙動を取得するためのより複雑なモデルは、複数の熱質量で構成されます。Segmented Rod モデルを開きます。

segmented_mass_model = 'HeatConductionThroughIronRodSegmented';
open_system(segmented_mass_model)

% Model parameters that are not already defined in the live script
num_segments = 9; % [-]

Segmented Rod サブシステムを開きます。

open_system([segmented_mass_model '/Segmented Rod'])

Segmented Rod モデルでは、直列に接続された 9 個のセグメントのセットとしてロッドを表します。各セグメントは単一の集中質量モデルと同じ構造を備えており、以下を含んでいます。

熱質量全体の ${1 / 9}^{th}$ である 1 つの熱質量
それぞれがロッドの長さの ${1 / 18}^{th}$ である 2 つの伝導伝熱素子
円柱面全体の ${1 / 9}^{th}$ の面積をもつ 1 つの対流伝熱素子。

この例では、厳密に 9 個のセグメントを選択する必要はありません。奇数のセグメントを選択すると、中間点にノードが配置されます。一般に、セグメント数を増やすと、解は解析解付近に収束します。十分な数のセグメントを追加した後にセグメントをさらに追加しても、収束性への影響はごくわずかです。この例を変更してセグメントを追加できます。

熱力学第一法則を使用して、各セグメントのノード温度の支配方程式を定義します。各セグメントで、内部エネルギーの変化率は、セグメントを通る正味熱流量に等しくなります。

$\frac{d U_{i}}{d t} = Q_{i}$ .

$i^{th}$ のセグメントに蓄積された内部エネルギーの変化率は次のとおりです。

$\frac{d U_{i}}{d t} = c m_{S e g m e n t} \frac{d T_{i}}{d t}$ ,

ここで、

$T_{i}$ は $i^{th}$ のノードの温度です。
$m_{Segment} = \frac{m}{9}$ は各セグメントの熱質量です。

セグメント 1 ～ 8 を通る熱流量は、左からの伝導、円柱面に沿った空気との対流、および右への伝導に起因します。 $9^{th}$ のセグメントの場合、右への熱流量の一部としてロッドの先端でも対流が発生します。

$Q_{i} = Q_{L e f t, i} + Q_{C y l, i} + Q_{R i g h t, i}$ .

左から $i^{th}$ のセグメントへの熱伝導は次のとおりです。

$Q_{L e f t, i} = k \frac{2 A}{L_{S e g m e n t}} (T_{i - 1} - T_{i})$ ,

ここで、

$L_{Segment} = \frac{L}{9}$ は各セグメントの長さです。

$i^{th}$ のセグメントの円柱面からの熱対流は次のとおりです。

$Q_{C y l, i} = h A_{C y l} (T_{A i r} - T_{i})$ .

ここで、

$A_{Cyl, Segment} = \frac{A_{Cyl}}{9}$ は各セグメントの円柱面の面積です。

${1 - 8}^{th}$ のセグメントの右への熱伝導は次のとおりです。

$Q_{R i g h t, i} = k \frac{2 A}{L_{S e g m e n t}} (T_{i + 1} - T_{i})$ ,

$9^{th}$ のセグメントの右への熱伝導と熱対流は次のとおりです。

$Q_{R i g h t, 9} = k \frac{2 A}{L_{S e g m e n t}} (T_{E n d} - T_{9})$ ,

$Q_{R i g h t, 9} = h A (T_{A i r} - T_{E n d})$ ,

ここで、 $T_{End}$ はロッドの先端の温度であり、ロッドの先端は Simscape モデル内の "Conduction9B" の B 端子と "Convection End" の A 端子のジャンクションに対応します。 $Q_{Right, 9}$ 方程式を並べ替えて $T_{End}$ を除外した後の、 $9^{th}$ のセグメントの右への熱流量は次のとおりです。

$Q_{R i g h t, 9} = \frac{2 A k h (T_{A i r} - T_{9})}{L h + 2 k}$ .

熱流量の式と熱質量の内部エネルギー変化の式をエネルギー保存の方程式に代入すると、ロッドを伝わる温度 $T_{i}$ の支配微分方程式になります。

$c m_{S e g m e n t} \frac{d T_{i}}{d t} = k \frac{2 A}{L_{S e g m e n t}} (T_{B a s e} - T_{i}) + h A_{C y l, S e g m e n t} (T_{A i r} - T_{i}) + \frac{2 A}{L_{S e g m e n t}} (T_{i + 1} - T_{i})$ ( $i = 1$ の場合)

$c m_{S e g m e n t} \frac{d T_{i}}{d t} = k \frac{2 A}{L_{S e g m e n t}} (T_{i - 1} - T_{i}) + h A_{C y l, S e g m e n t} (T_{A i r} - T_{i}) + \frac{2 A}{L_{S e g m e n t}} (T_{i + 1} - T_{i})$ ( $i = 2 to 8$ の場合)

$c m_{S e g m e n t} \frac{d T_{i}}{d t} = k \frac{2 A}{L_{S e g m e n t}} (T_{i - 1} - T_{i}) + h A_{C y l, S e g m e n t} (T_{A i r} - T_{i}) + \frac{2 A k h (T_{A i r} - T_{i})}{L h + 2 k}$ ( $i = 9$ の場合)

Simscape ネットワークはノードにおける熱伝達を合計しますが、これはこれらの微分方程式と等価です。

$i^{th}$ のノード温度の変化率は、隣接ノード ( ${i - 1}^{th}$ と ${i + 1}^{th}$ ) の温度によって異なります。各セグメントの熱質量により、セグメントの温度変化率が低下します。これらの特性により、モデルはロッドを徐々に伝わる熱波の影響を取得できます。

Rod モデルのシミュレーションと比較

モデルをシミュレートし、シミュレーション出力を取得します。

% Simulate the single lumped mass model
open_system(lumped_mass_model);
sim(lumped_mass_model);

% Get the simulation outputs
T_Lumped = yout_lumped_mass_model(:,1); % Sensed temperature [degC]
Q_Lumped = yout_lumped_mass_model(:,2); % Sensed base heat transfer rate [W]
time_Lumped = tout_lumped_mass_model;   % [sec]

% Simulate the segmented mass model
open_system(segmented_mass_model);
sim(segmented_mass_model);

% Get the simulation outputs
T_Segmented = yout_segmented_mass_model(:,1:5); % Sensed temperatures [degC]
Q_Segmented = yout_segmented_mass_model(:,6);   % Sensed base heat transfer rate [W]
time_Segmented = tout_segmented_mass_model;     % [sec]

シミュレートされた温度

シミュレートされた温度をプロットします。

figure;
clf;
hold on;
plot(time_Lumped, T_Lumped, '--', 'Color', [0.49 0.18 0.56])
plot(time_Segmented, T_Segmented);
xlabel('Time (sec)')
title('Temperature (degC)')
legend('Lumped rod (midpoint)', 'Segment 1', 'Segment 3', 'Segment 5 (midpoint)', 'Segment 7', 'Segment 9', 'Location', 'best')

このプロットは、単一の集中質量の Rod モデルと Segmented Rod モデルにおける熱質量のシミュレートされた温度を示しています。

Segmented Rod モデルは、単一質量の Rod モデルでは無視される次のような影響をいくつか取得しています。高温ベースから離れているセグメントは、温度が上昇し始める前の遅延が長くなっています。複数のセグメントを使用すると、ロッドに沿った温度勾配も測定できます。高温ベースから離れているセグメントは、高温ベースに近いセグメントよりも定常状態の温度が低くなっています。

一方、はるかに単純な単一の集中質量モデルは、ロッドの中間点の全般的な温度挙動を取得しており、シミュレーションのコストが低くなっています。プロットから、単一の集中質量モデルが定常状態の中間点温度を低く見積もっていることがわかります。定常状態の中間点温度が異なるのは、単一の集中質量系が円柱面全体の温度を中間点温度と等しいものとしてモデル化するためです。したがって、ベースと中間点の間の対流熱伝達を低く、中間点と先端の間の対流熱伝達を高く見積もります。

ベースの熱伝達

シミュレートされたベースの熱伝達率をプロットします。

figure;
clf;
hold on;
plot(time_Lumped, Q_Lumped, '--')
plot(time_Segmented, Q_Segmented);
xlabel('Time (sec)')
title('Base Heat Flow')
legend('Lumped rod', 'Segmented rod', 'Location', 'best')

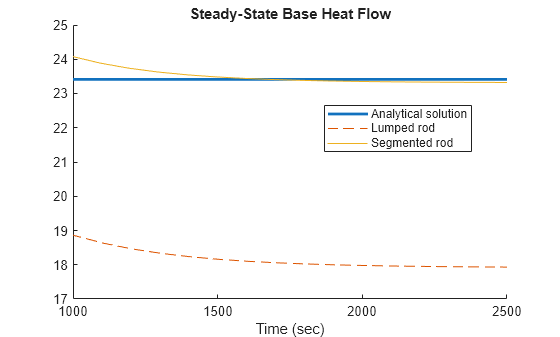
このプロットは、両方のモデルについてのベースからロッドへのシミュレートされた熱伝達を示しています。単一の集中質量モデルは、Segmented Rod モデルと比較して熱伝達を低く見積もります。単一の集中質量モデルは、円柱面全体の対流を、ロッドの分布点と空気の間としてではなくロッドの中間点と空気の間としてモデル化することで、ロッドの熱抵抗を高く見積もります。高温ベースに近いロッドの点は、ベースからさらに離れている点よりも温度が高くなるため、対流熱伝達が向上します。

計算コスト

単一の集中質量の Rod モデルには 1 つの微分変数が含まれ、Segmented Rod モデルには 9 つの微分変数、つまり系内の熱質量 (自由度) ごとに 1 つの微分変数が含まれています。微分変数が多く含まれるモデルは計算コストが高くなり、シミュレーションに必要な計算能力も高くなる傾向があります。

Simscape の統計ビューアーを見ると、各モデル内の微分変数の数がわかります。モデル統計を表示するために、モデルウィンドウの [デバッグ] タブで、[Simscape]、[統計ビューアー] をクリックします。

忠実度の高いシミュレーションのために、セグメント数を 9 より多くすることができます。

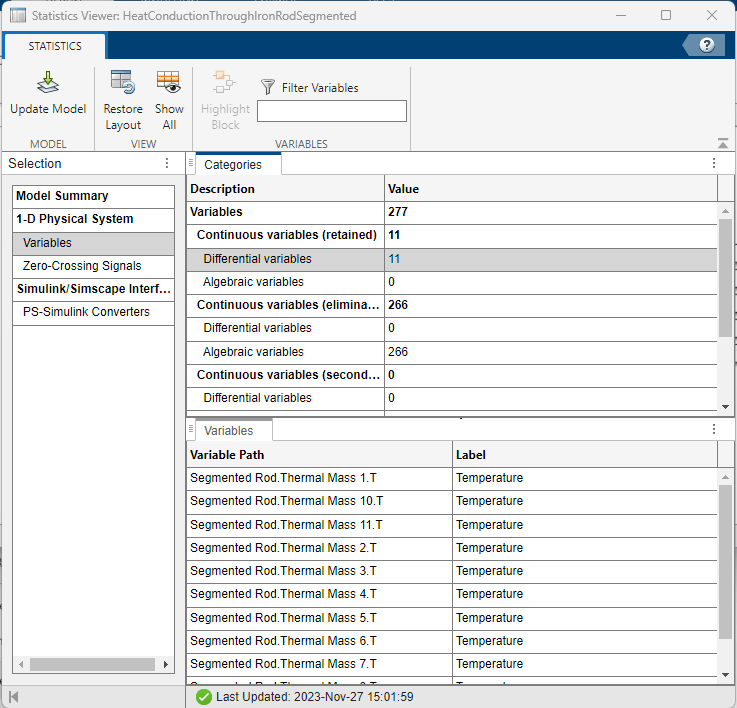
定常状態の解析解との比較

一定の断面積がその長さに沿った伝導と対流を受けるロッドの場合、ロッドを伝わる定常状態の温度を決定する微分方程式は次のとおりです。

$\frac{d^{2} T}{d x^{2}} - \frac{h π D x}{k A} (T - T_{A i r}) = 0$ ,

ここで、 $x$ はベースからの縦方向の距離です。

この例では、次の境界条件をもつロッドについて考えます。

ベースの温度が $T (0) = T_{B}$ で固定されている。
ロッドの先端で、伝導による熱伝達が対流による熱伝達と等しい

$hA (T_{Air} - T (L)) = kA \frac{dT (L)}{dx}$

与えられた境界条件に従う線形で同次の 2 階微分方程式の解は次のとおりです [1]:

$T (x) = \frac{cosh m (L - x) + (h / m k) sinh m (L - x)}{cosh m L + (h / m k) sinh m L} (T_{B} - T_{A i r}) + T_{A i r}$ ,

ここで、

$m^{2} = \frac{h π D}{kA}$ .

ロッドのベースを通じた熱伝達率は次のとおりです。

$Q_{B a s e} = \sqrt{h π D k A} (T_{B} - T_{A i r}) \frac{sinh m L + (h / m k) cosh m L}{cosh m L + (h / m k) sinh m L}$

[1] Incropera, DeWitt, Bergman, Lavine, "Fundamentals of Heat and Mass Transfer". 6th Ed, Section 3.6. John Wiley & Sons, 2006.

ロッドのパラメーターについて定常状態の解析温度と熱流量を計算します。

% Temperature at the mid-point
x = L/2;
m_eqn = sqrt(h*pi*D/(k*A));
T_mid_analytical_ss = ( cosh(m_eqn*(L-x)) + h/(m_eqn*k) * sinh(m_eqn*(L-x)) ) / ( cosh(m_eqn*L) + h/(m_eqn*k) * sinh(m_eqn*L) ) * (T_base - T_air) + T_air % [degC]

T_mid_analytical_ss = 60.9884

% heat flow out the base
Q_base_analytical_ss = sqrt(h*pi*D*k*A)*(T_base-T_air) * ( sinh(m_eqn*L) + h/(m_eqn*k) * cosh(m_eqn*L) ) / ( cosh(m_eqn*L) + h/(m_eqn*k) * sinh(m_eqn*L) ) % [W]

Q_base_analytical_ss = 23.4123

定常状態の解析解とシミュレートされた解をプロットします。以下のプロットは、9 個のセグメントをもつセグメント化モデルが解析解でほぼ収束しているのに対し、単一の集中質量モデルが誤差を保持していることを示しています。セグメント数を増やすと、解析予測での収束性がさらに向上します。

figure;
clf;
hold on;
plot([1000 2500], T_mid_analytical_ss*[1 1], 'LineWidth', 2)
plot(time_Lumped, T_Lumped, '--', 'Color', [0 0.6 0])
plot(time_Segmented, T_Segmented);
xlabel('Time (sec)')
title('Steady-State Temperature (degC)')
legend('Analytical solution', 'Lumped rod (midpoint)', 'Segment 1', 'Segment 3', 'Segment 5 (midpoint)', 'Segment 7', 'Segment 9', 'Location', 'best')
xlim([1000 2500]) % Zoom into the steady-state time region

% Plot the base heat transfer rate
figure;
clf;
hold on;
plot([1000 2500], Q_base_analytical_ss*[1 1], 'LineWidth', 2)
plot(time_Lumped, Q_Lumped, '--')
plot(time_Segmented, Q_Segmented);
xlabel('Time (sec)')
title('Steady-State Base Heat Flow')
legend('Analytical solution', 'Lumped rod', 'Segmented rod', 'Location', 'best')
xlim([1000 2500]) % Zoom into the steady-state time region