周期的波形の RMS 値

この例では、rms を使用して、正弦波、方形波および矩形パルス列の平方根平均二乗 (RMS) 値を求める方法を説明します。この例の波形は、上記波形の連続時間相当の離散時間バージョンです。

$π / 4$ ラジアン/サンプルの周波数を持つ正弦波を作成します。信号の長さは 16 サンプルとし、これは正弦波の 2 周期に相当します。

n = 0:15;
x = cos(pi/4*n);

正弦波の RMS 値を計算します。

rmsval = rms(x)

rmsval = 0.7071

RMS 値は、予想どおり $1 / \sqrt 2$ に等しくなります。

0.1 秒の周期をもつ方形波を作成します。方形波の値は $- 2$ と $2$ の間で振動します。

t = 0:0.01:1;
x = 2*square(2*pi*10*t);

stem(t,x,'filled')
axis([0 1 -2.5 2.5])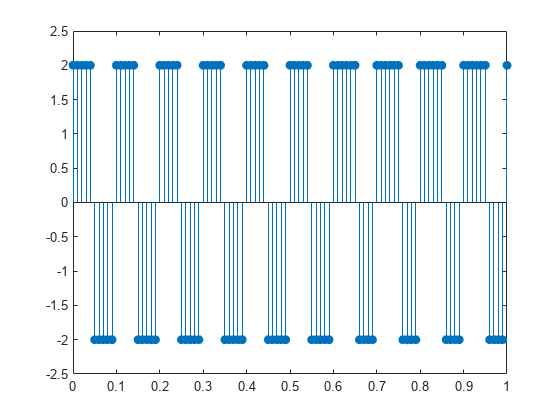

RMS 値を求めます。

rmsval = rms(x)

rmsval = 2

RMS 値は、理論値の 2 に一致します。

各 0.1 秒区間におけるパルスを 0.025 秒間はオン (値 1)、0.075 秒間はオフ (値 0) とするパラメーター設定で、1 kHz でサンプリングされた矩形パルス列を作成します。このことは、パルス周期は 0.1 秒、パルスがオンになるのはその区間の 1/4 であることを意味します。これは、"デューティ比" と呼ばれます。pulstran を使用して矩形パルス列を作成します。

t = 0:0.001:(10*0.1);
pulsewidth = 0.025;
pulseperiods = [0:10]*0.1;
x = pulstran(t,pulseperiods,@rectpuls,pulsewidth);

plot(t,x)
axis([0 1 -0.5 1.5])

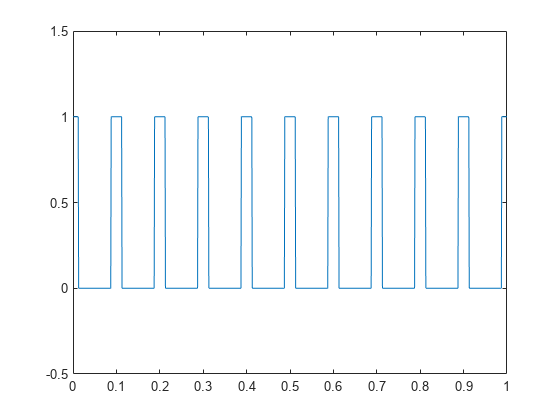
RMS 値を求め、それをデューティ比 1/4、ピーク振幅 1 の連続時間矩形パルス波形の RMS 値と比較します。

rmsval = rms(x)

rmsval = 0.5007

thrms = sqrt(1/4)

thrms = 0.5000

観測された RMS 値と連続時間矩形パルス波形の RMS 値はよく一致しています。