周波数領域の線形回帰

ライブスクリプトを開く

この例は、離散フーリエ変換を使用して、時系列に対する線形回帰モデルを作成する方法を示しています。この例で使用する時系列は、米国における 1973 年から 1979 年までの月ごとの事故死亡者数です。データは Brockwell and Davis (2006) により公表されています。一次資料は、米国安全性評議会のものです。

データを入力します。行列 exdata を MATLAB® ワークスペースにコピーします。

exdata = [
        9007        7750        8162        7717        7792        7836
        8106        6981        7306        7461        6957        6892
        8928        8038        8124        7776        7726        7791
        9137        8422        7870        7925        8106        8129
       10017        8714        9387        8634        8890        9115
       10826        9512        9556        8945        9299        9434
       11317       10120       10093       10078       10625       10484
       10744        9823        9620        9179        9302        9827
        9713        8743        8285        8037        8314        9110
        9938        9129        8433        8488        8850        9070
        9161        8710        8160        7874        8265        8633
        8927        8680        8034        8647        8796        9240];

exdata は 12 行 6 列の行列です。exdata の各列は 12 か月のデータを含みます。各列の 1 番目の行は、対応する年の 1 月の米国における事故死亡者数を含みます。各列の最後の行は、対応する年の 12 月の米国における事故死亡数を含みます。

データ行列を 72 行 1 列の時系列に変更して、1973 年から 1978 年までの間のデータをプロットします。

ts = reshape(exdata,72,1);
years = linspace(1973,1979,72);

plot(years,ts,'o-','MarkerFaceColor','auto')
xlabel('Year')
ylabel('Number of Accidental Deaths')

Figure contains an axes object. The axes object with xlabel Year, ylabel Number of Accidental Deaths contains an object of type line.

データを目視すると、事故死亡者数は周期的に変動していることがわかります。変動の周期は約 1 年 (12 か月) です。データの周期的な性質により、適切なモデルは

$X (n) = μ + \sum_{k} (A_{k} \cos \frac{2 π k n}{N} + B_{k} \cos \frac{2 π k n}{N}) + ε (n),$

ここで、 $μ$ は全平均、 $N$ は時系列の長さ、 $ε (n)$ はゼロ平均でいくつかの分散をもち、互いに独立で同一の分布に従う (IID) ガウス確率変数のホワイトノイズ列です。加法性ノイズの項は、データ固有のランダム性に相当します。モデルのパラメーターは全平均および余弦関数と正弦関数の振幅です。モデルは、パラメーターに関して線形です。

時間領域における線形回帰モデルを作成するためには、余弦関数と正弦関数で使用する周波数を指定し、計画行列を形成し、モデルパラメーターの最小二乗推定を得るための正規方程式を解く必要があります。この場合、離散フーリエ変換を使用して周期性を検出し、フーリエ係数のサブセットだけを残して逆変換を行って、時系列の近似を求めるほうが簡単です。

データのスペクトル解析を行って、どの周波数がデータの変動に大きく寄与しているかを明らかにします。信号の全平均は約 9,000 で、それは周波数 0 におけるフーリエ変換に比例するので、スペクトル解析の前に平均を減算します。これによって周波数 0 における大きな振幅のフーリエ係数を削除し、顕著な変動を検出しやすくします。フーリエ変換の周波数は、時系列の長さの逆数である 1/72 間隔で配置されます。月ごとにデータをサンプリングしているので、スペクトル解析における最も高い周波数は 1/2 サイクル/月です。この場合、可視化のため、サイクル/年を単位としてスペクトル解析をとらえ、対応する周波数にスケーリングするのが便利です。

tsdft = fft(ts-mean(ts));
freq = 0:1/72:1/2;

plot(freq.*12,abs(tsdft(1:length(ts)/2+1)),'o-', ...
    'MarkerFaceColor','auto')
xlabel('Cycles/Year')
ylabel('Magnitude')
ax = gca;
ax.XTick = [1/6 1 2 3 4 5 6];

Figure contains an axes object. The axes object with xlabel Cycles/Year, ylabel Magnitude contains an object of type line.

振幅を基準にすると、12 か月を 1 サイクルとする場合の周波数がデータにおいて最も大きな変動になります。1 サイクルが 12 か月である場合、振幅は他の 2 倍を上回っています。ただし、スペクトル解析は、データには他にも周期的な成分があることを明らかにしています。たとえば、1 サイクル/12 か月の高調波 (整数倍) において周期的な成分があるように見えます。また、1 サイクル/72 か月の周期で周期的な成分があるように見えます。

データのスペクトル解析に基づいて、最も大きな成分の周波数をもつ余弦項および正弦項を使用して、単純な線形回帰モデルを近似します。ここで最も大きな成分の周波数は、次のとおりです。1 サイクル/年 (1 サイクル/12 か月)。

1 サイクル/12 か月に対応する離散フーリエ変換の周波数ビンを決定します。周波数は 1/72 間隔で配置され、最初のビンは周波数 0 に対応するので、正確なビンは 72/12+1 です。これは、"正の" 周波数の周波数ビンです。"負の" 周波数に対応する周波数ビンも含めなければなりません。負の周波数は -1 サイクル/12 か月です。MATLAB インデックスでは、負の周波数の周波数ビンは 72-72/12+1 です。

72 行 1 列の 0 のベクトルを作成します。ベクトルの適切な要素に、1 サイクル/12 か月の正と負の周波数に対応するフーリエ係数を入れます。フーリエ変換の逆変換を行ってから全平均を加えて、事故死亡者数データの近似を求めます。

freqbin = 72/12;
freqbins = [freqbin 72-freqbin]+1;
tsfit = zeros(72,1);
tsfit(freqbins) = tsdft(freqbins);
tsfit = ifft(tsfit);
mu = mean(ts);
tsfit = mu+tsfit;

元のデータを 2 つのフーリエ係数を使用した時系列近似とともにプロットします。

plot(years,ts,'o-','MarkerFaceColor','auto')
xlabel('Year')
ylabel('Number of Accidental Deaths')
hold on
plot(years,tsfit,'linewidth',2)
legend('Data','Fitted Model')
hold off

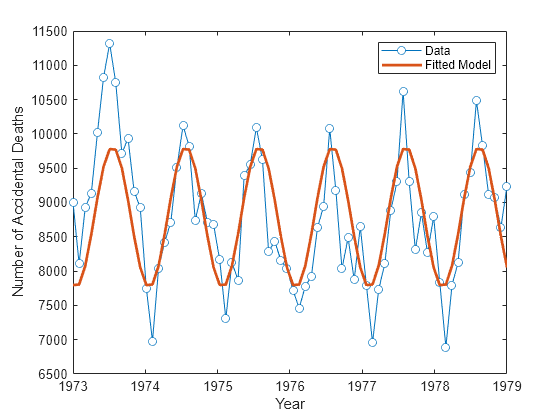
Figure contains an axes object. The axes object with xlabel Year, ylabel Number of Accidental Deaths contains 2 objects of type line. These objects represent Data, Fitted Model.

近似モデルはデータの周期性をおおまかにとらえて表示し、データが 1 年周期で変動しているという最初の結論をサポートします。

1 サイクル/12 か月の 1 つの周波数が、観測された時系列をどの程度適切に説明しているかを評価するために、残差を求めます。残差がホワイトノイズ列に類似している場合、1 つの周波数をもつ単純な線形モデルは時系列を適切にモデル化していることになります。

残差を評価するために、ホワイトノイズに対して 95% の信頼区間をもつ自己相関列を使用します。

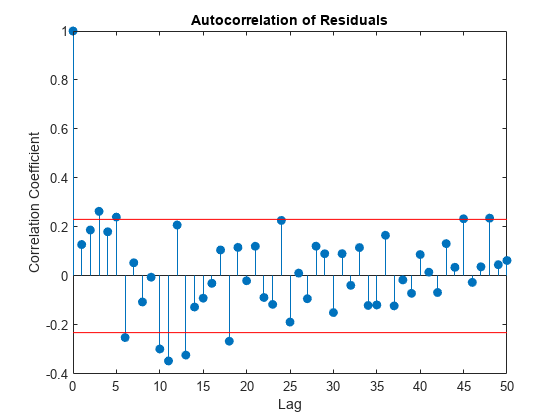
resid = ts-tsfit;
[xc,lags] = xcorr(resid,50,'coeff');

stem(lags(51:end),xc(51:end),'filled')
hold on
lconf = -1.96*ones(51,1)/sqrt(72);
uconf = 1.96*ones(51,1)/sqrt(72);
plot(lags(51:end),lconf,'r')
plot(lags(51:end),uconf,'r')
xlabel('Lag')
ylabel('Correlation Coefficient')
title('Autocorrelation of Residuals')
hold off

Figure contains an axes object. The axes object with title Autocorrelation of Residuals, xlabel Lag, ylabel Correlation Coefficient contains 3 objects of type stem, line.

自己相関の値は、多くのラグにおいて 95% 信頼限界の外側にあります。残差がホワイトノイズであるようには見えません。結論は、1 つの正弦波成分をもつ簡単な線形モデルは、事故死亡者数におけるすべての振動については説明していないということです。スペクトル解析により主要な振動の他に周期的な成分があることが明らかになっていたため、このことは予期されていました。スペクトル解析によって示された他の周期項を組み込んだモデルを作成することにより、近似が改善され、残差が白色化されます。

フーリエ係数の振幅の大きいものから 3 個が含まれているモデルの近似を行います。正と負の両方の周波数に対応するフーリエ係数を残す必要があるので、大きいものから 6 個を残します。

tsfit2dft = zeros(72,1);
[Y,I] = sort(abs(tsdft),'descend');
indices = I(1:6);
tsfit2dft(indices) = tsdft(indices);

72 個のフーリエ係数のうちの 6 個 (3 つの周波数) だけを残したものが、信号のエネルギーの大部分を保持していることを示します。最初に、フーリエ係数をすべて残したものでは、元の信号とフーリエ変換のエネルギーが等価になることを示します。

norm(1/sqrt(72)*tsdft,2)/norm(ts-mean(ts),2)

ans = 1.0000

比率は 1 です。次に、3 つの周波数だけを残したもののエネルギー比を調べます。

norm(1/sqrt(72)*tsfit2dft,2)/norm(ts-mean(ts),2)

ans = 0.8991

エネルギーのほぼ 90% が保持されています。同様に、時系列の分散の 90% が 3 つの周波数成分によって説明されます。

3 つの周波数成分に基づくデータの推定を行います。元のデータ、1 つの周波数をもつモデルおよび 3 つの周波数をもつモデルを比較します。

tsfit2 = mu+ifft(tsfit2dft,'symmetric');

plot(years,ts,'o-','markerfacecolor','auto')
xlabel('Year')
ylabel('Number of Accidental Deaths')
hold on
plot(years,tsfit,'linewidth',2)
plot(years,tsfit2,'linewidth',2)
legend('Data','1 Frequency','3 Frequencies')
hold off

Figure contains an axes object. The axes object with xlabel Year, ylabel Number of Accidental Deaths contains 3 objects of type line. These objects represent Data, 1 Frequency, 3 Frequencies.

3 つの周波数を使用することで、元の信号への近似が改善されます。このことは、3 つの周波数を使用したモデルの残差の自己相関を調べることによってわかります。

resid = ts-tsfit2;
[xc,lags] = xcorr(resid,50,'coeff');

stem(lags(51:end),xc(51:end),'filled')
hold on
lconf = -1.96*ones(51,1)/sqrt(72);
uconf = 1.96*ones(51,1)/sqrt(72);
plot(lags(51:end),lconf,'r')
plot(lags(51:end),uconf,'r')
xlabel('Lag')
ylabel('Correlation Coefficient')
title('Autocorrelation of Residuals')
hold off

Figure contains an axes object. The axes object with title Autocorrelation of Residuals, xlabel Lag, ylabel Correlation Coefficient contains 3 objects of type stem, line.

3 つの周波数を使用することで、残差がホワイトノイズ過程により近づいているという結果になっています。

フーリエ変換によって求められたパラメーター値は、時間領域の線形回帰モデルと等価であることを示します。計画行列を形成して正規方程式を解くことによって、3 つの周波数に対する全平均、余弦関数振幅および正弦関数振幅について、最小二乗推定を求めます。近似による時系列を、フーリエ変換によって求められた時系列と比較します。

X = ones(72,7);
X(:,2) = cos(2*pi/72*(0:71))';
X(:,3) = sin(2*pi/72*(0:71))';
X(:,4) = cos(2*pi*6/72*(0:71))';
X(:,5) = sin(2*pi*6/72*(0:71))';
X(:,6) = cos(2*pi*12/72*(0:71))';
X(:,7) = sin(2*pi*12/72*(0:71))';
beta = X\ts;
tsfit_lm = X*beta;
max(abs(tsfit_lm-tsfit2))

ans = 7.2760e-12

2 つの方法は同じ結果になります。2 つの波形における差の最大絶対値は約 10 ～12 です。このようなケースについては、周波数領域でのアプローチのほうがこれに対応する時間領域でのアプローチよりも容易でした。スペクトル解析を使用すれば、どの変動がデータ中に現れるかは必然的に目視で検査されます。このステップから考えて、余弦関数と正弦関数の和からなる信号に対しては、フーリエ係数を使用したモデル構築が簡単です。

時系列のスペクトル解析および時間領域の回帰との等価性についての詳細については、「Shumway and Stoffer (2006)」を参照してください。

スペクトル解析は、どの周期的な成分がデータの多様性に顕著に寄与しているかに答えることができますが、なぜこういった成分が存在するかは説明しません。これらのデータを詳しく調べると、12 か月周期において最小値は 2 月に現れやすく、最大値は 7 月に現れやすいことがわかります。これらのデータについて考えられる説明は、人は生まれつき冬よりも夏に活動的であるということです。不幸にも、この活動性の増加の結果、死亡事故の発生確率が増加しています。

参考文献

Brockwell, Peter J., and Richard A. Davis. Time Series: Theory and Methods. New York: Springer, 2006.

Shumway, Robert H., and David S. Stoffer. Time Series Analysis and Its Applications with R Examples. New York: Springer, 2006.

参考

fft | ifft | xcorr