歪みの測定

50 kHz でサンプリングされた周波数 2.5 kHz の正弦波のサンプルを 2048 個生成します。S/N 比 (SNR) が 80 dB となるホワイト ガウス ノイズを付加します。

Fs = 5e4; 
f0 = 2.5e3;
N = 2048;
t = (0:N-1)/Fs;
SNR = 80;

x = cos(2*pi*f0*t);
x = x+randn(size(x))*std(x)/db2mag(SNR);

結果を多項式で表される弱非線形増幅器に通します。増幅器によって高調波の周波数にスプリアス トーンが発生します。

amp = [1e-5 5e-6 -1e-3 6e-5 1 25e-3];
x = polyval(amp,x);

信号スペクトルをプロットして SNR に注釈を付け、期待値に達していることを確認します。関数 snr は、基本波のノイズ フロアに対するパワー比率を計算し、DC 成分と高調波を無視します。

snr(x,Fs);

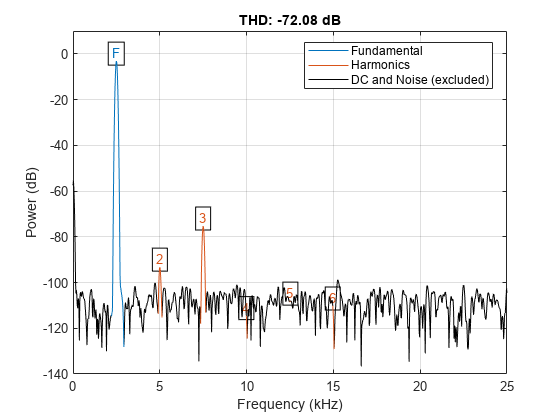
信号スペクトルをプロットし、全高調波歪み (THD) に注釈を付けます。関数 thd は、高調波の基本波に対するパワー比率を計算し、DC 成分とノイズ フロアを無視します。

thd(x,Fs);

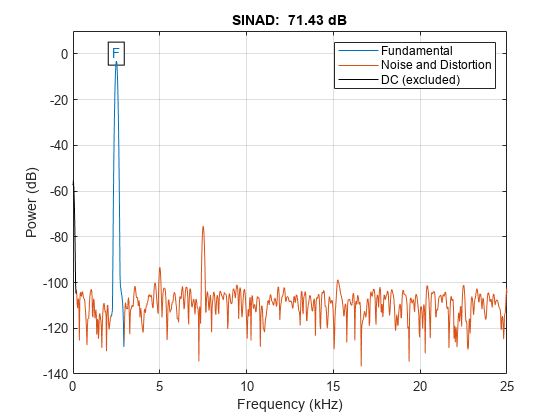
信号スペクトルをプロットし、信号対ノイズおよび歪みの比率 (SINAD) に注釈を付けます。関数 sinad は、基本波の高調波とノイズ フロアに対するパワー比率を計算します。ここでは DC 成分のみが無視されます。

sinad(x,Fs);

SNR、THD および SINAD が以下の方程式に従っていることを検証します。

$$10^{-SNR/10}+10^{THD/10}=10^{-SINAD/10}.$$

lhs = 10^(-snr(x,Fs)/10)+10^(thd(x,Fs)/10)

lhs = 7.2203e-08

rhs = 10^(-sinad(x,Fs)/10)

rhs = 7.1997e-08

信号スペクトルをプロットし、スプリアスフリー ダイナミック レンジ (SFDR) に注釈を付けます。SFDR は、基本波と最強のスプリアス成分 ("スパー") のパワー比率です。この例では、スパーは第 3 高調波に対応します。

sfdr(x,Fs);

参考

sfdr | sinad | snr | thd