pkurtosis

(削除予定) 信号またはスペクトログラムからのスペクトル尖度

pkurtosis は将来のリリースで削除される予定です。代わりに spectralKurtosis を使用してください。詳細については、バージョン履歴を参照してください。

構文

sk = pkurtosis(x)

sk = pkurtosis(x,sampx)

sk = pkurtosis(xt)

sk = pkurtosis(___,window)

sk = pkurtosis(s,sampx,f,window)

[sk,fout] = pkurtosis(___)

[___,thresh] = pkurtosis(___,'ConfidenceLevel',p)

pkurtosis(___)

説明

sk = pkurtosis(x) は、ベクトル x のスペクトル尖度をベクトル sk として返します。pkurtosis は、正規化周波数 (範囲 [0 π] に等間隔に並んだ周波数ベクトル) を使用して時間値を計算します。pkurtosis は、既定のウィンドウ サイズ (サンプル単位の時間分解能)、および 80% ウィンドウ オーバーラップで pspectrum を使用して x のスペクトログラムを計算します。

sk = pkurtosis(x,sampx) は、sampx のレートまたは時間間隔でサンプリングされた、ベクトル x のスペクトル尖度を返します。

sk = pkurtosis(xt) は、ベクトル sk 内の単一変数 timetable xt のスペクトル尖度を返します。xt は増加する有限の時間サンプルを含まなければなりません。

sk = pkurtosis(___,window) は、pspectrum スペクトログラム計算の window で指定した時間分解能を使用してスペクトル尖度を返します。window は、これより前の構文の任意の入力引数と共に使用できます。

sk = pkurtosis(s,sampx,f,window) は、スペクトログラムまたはパワー スペクトログラム s を以下と共に使用してスペクトル尖度を返します。

• s を生成するために変換された元の時系列信号のサンプル レートまたは時間、sampx

• スペクトログラム周波数ベクトル f

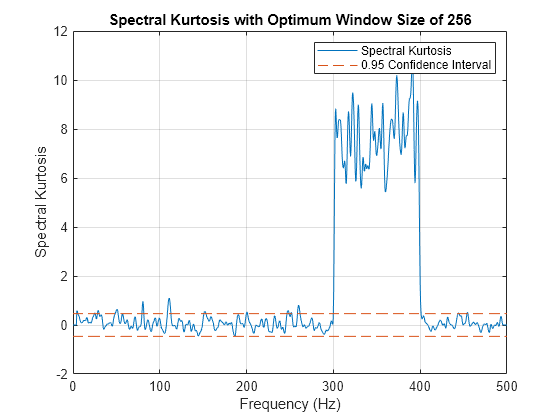
• スペクトログラム時間分解能 window

pkurtosis を適用する既定の pspectrum オプションを受け入れるのではなく pspectrum のオプションをカスタマイズする場合は、この構文を使用します。sampx を空として指定すると既定の正規化周波数に設定できます。これより前の構文では window はオプションですが、この構文を使用する場合は window の値を指定しなければなりません。

[sk,fout] = pkurtosis(___) は、スペクトル尖度 sk を周波数ベクトル fout と共に返します。これらの出力引数は、これより前の構文の任意の入力引数と共に使用できます。

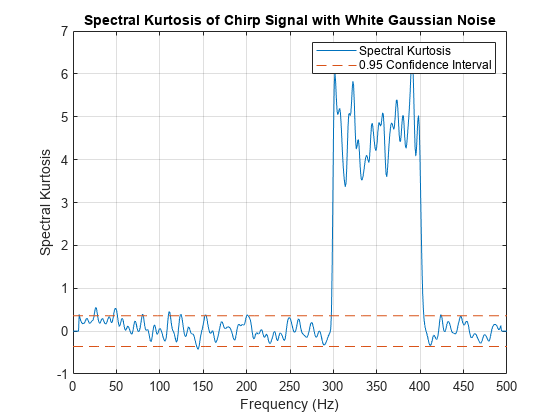
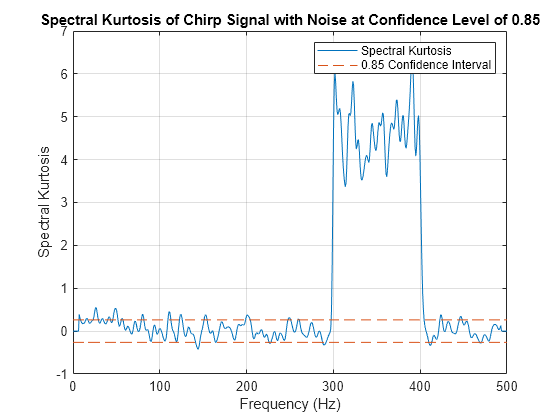
[___,thresh] = pkurtosis(___,'ConfidenceLevel',p) は、信頼度 p を使用してスペクトル尖度しきい値 thresh を返します。thresh は、指定または既定の設定で受け入れたオプションの信頼度 p において、スペクトル尖度がガウス定常信号を示す範囲を表します。p を指定することで、スペクトル尖度 thresh の結果の感度を調整して、非ガウスまたは非定常の動作になるようにできます。thresh 出力引数は、これより前の構文の任意の入力引数と共に使用できます。前の構文では信頼度を設定することもできますが、thresh を返すかまたはプロットを行わないと効果はありません。

pkurtosis(___) は、スペクトル尖度を信頼度およびしきい値と共にプロットし、データは返しません。この構文は、これより前の構文の任意の入力引数で使用できます。

例

異なる信頼度を使用した非定常信号のスペクトル尖度のプロット

ホワイト ノイズ内のチャープ信号のスペクトル尖度をプロットし、非定常、非ガウス状態をどのように検出できるかを確認します。信頼度の変化と正規化周波数の発動の影響を調べます。

チャープ信号を作成し、ホワイト ガウス ノイズを追加して、プロットします。

fs = 1000;
t = 0:1/fs:10;
f1 = 300;
f2 = 400;

xc = chirp(t,f1,10,f2);
x = xc + randn(1,length(t));

plot(t,x)
title('Chirp Signal with White Gaussian Noise')

信号のスペクトル尖度をプロットします。

pkurtosis(x,fs)
title('Spectral Kurtosis of Chirp Signal with White Gaussian Noise')

プロットは、300 ～ 400 Hz で、はっきりと広がった偏位を示します。この偏位は、非定常チャープを表す信号成分に対応します。2 本の水平方向の赤い破線の間の領域は、確率的定常およびガウス動作の区域を意味し、0.95 信頼区間で定義されています。この区域内のどの尖度ポイントの立ち下がりも、高い可能性で定常またはガウスです。この区域外の尖度ポイントは、非定常または非ガウスとしてフラグが付けられています。300 Hz 未満では、区域の上しきい値の少し上にさらにいくつかの偏位があります。これらの偏位は偽陽性を表し、信号は定常でガウスであるにもかかわらず、ノイズが原因でしきい値を超えています。

信頼度を既定の設定の 0.95 から 0.85 に変更してその影響を調査します。

pkurtosis(x,fs,'ConfidenceLevel',0.85)
title('Spectral Kurtosis of Chirp Signal with Noise at Confidence Level of 0.85')

信頼度の低さは、非定常または非ガウス周波数成分の検出の感度がより高いことを意味します。信頼度を下げると、thresh で区切られた区域が縮小します。ここで低レベルの偏位 — 偽警報 — は、数と量の両方において増加しています。信頼度を設定して、効果的な検出の実現と、偽陽性数の制限との間のバランスをとることができます。

信頼度を返す pkurtosis 形式を使用して、2 つのケースの区域の幅を正確に決定して比較することができます。

[sk1,~,thresh95] = pkurtosis(x);
[sk2,~,thresh85] = pkurtosis(x,'ConfidenceLevel',0.85);
thresh = [thresh95 thresh85]

thresh = 1×2

    0.3578    0.2628

スペクトル尖度をもう一度プロットしますが、今度は、pkurtosis で正規化周波数がプロットされるようにサンプル時間の情報を省略します。

pkurtosis(x,'ConfidenceLevel',0.85)
title('Spectral Kurtosis using Normalized Frequency')

周波数軸が Hz から 0 ～ π ラジアン/サンプルによるスケールに変わりました。

カスタム ウィンドウ サイズを使用したスペクトル尖度のプロット

関数 pkurtosis は、既定の pspectrum ウィンドウ サイズ (時間分解能) を使用します。代わりにウィンドウ サイズを指定して使用できます。この例では、最適なウィンドウ サイズを返す関数 kurtogram を使用し、その結果を pkurtosis に使用します。

ホワイト ガウス ノイズを含むチャープ信号を作成します。

fs = 1000;
t = 0:1/fs:10;
f1 = 300;
f2 = 400;
x = chirp(t,f1,10,f2)+randn(1,length(t));

既定のウィンドウ サイズを使用してスペクトル尖度をプロットします。

pkurtosis(x,fs)
title('Spectral Kurtosis with Default Window Size')

ここで kurtogram を使用して最適なウィンドウ サイズを計算します。

kurtogram(x,fs)

また kurtogram プロットは、300 から 400 Hz の範囲のチャープも示して最適なウィンドウ サイズが 256 であることを示します。w0 を pkurtosis に入力します。

w0 = 256;
pkurtosis(x,fs,w0)
title('Spectral Kurtosis with Optimum Window Size of 256')

主な偏位には高い尖度値があります。高い値は、定常成分と非定常成分との間の区別を改善し、非定常成分を特徴として抽出する能力を向上させます。

カスタム スペクトログラムを使用したスペクトル尖度のプロット

信号入力データを使用する場合、pkurtosis は、既定のオプションで pspectrum を使用することでスペクトログラムを生成します。オプションをカスタマイズしてスペクトログラムを自分で作成することもできます。

ホワイト ガウス ノイズを含むチャープ信号を作成します。

fs = 1000;
t = 0:1/fs:10;
f1 = 300;
f2 = 400;
x = chirp(t,f1,10,f2)+randn(1,length(t));

独自のウィンドウ、オーバーラップ、および FFT 点の数の仕様を用いてスペクトログラムを生成します。その後、そのスペクトログラムを pkurtosis で使用します。

window = 256;
overlap = round(window*0.8);
nfft = 2*window;
[s,f,t] = spectrogram(x,window,overlap,nfft,fs);
figure
pkurtosis(s,fs,f,window)

偏位の振幅がより大きいため、前の例の既定の入力よりも偏差が大きくなります。ただし、ここの偏位の振れ幅は kurtogram 最適化ウィンドウの例ほど大きくはありません。

入力引数

x — 時系列の信号

ベクトル

pkurtosis がスペクトル尖度を返す元となる、時系列の信号です。ベクトルで指定します。

sampx — 信号のサンプル レートまたはサンプル時間

正規化周波数 (既定値) | 正の数値スカラー | duration スカラー | 秒単位での数値ベクトル | duration 配列 | datetime 配列

サンプル レートまたはサンプル時間。以下のいずれかで指定します。

• 正の数値スカラー — Hz 単位での周波数

• duration スカラー — X の連続するサンプル間の時間間隔

• ベクトル、duration 配列、または datetime 配列 — x の各要素に対応する時点または持続時間

sampx が時間ベクトルを表す場合、時間サンプルは不等間隔で構いませんが、時間間隔の中央値と時間間隔の平均値は以下に従わなければならないという pspectrum の制約があります。

$$\frac{1}{100}<\frac{\text{Median time interval}}{\text{Mean time interval}}<100.$$

sampx を空として指定した場合、pkurtosis は正規化周波数を使用します。言い換えれば、範囲 [0 π] に等間隔に並んだ周波数ベクトルが想定されます。

xt — 信号 timetable

timetable

pkurtosis がスペクトル尖度を返す元となる信号 timetable。単一の列で単一の変数を含む timetable で指定します。xt は、増加する、有限の行時間でなければなりません。timetable に時点がないまたは重複している場合、欠損または重複する時間および非等間隔の時間をもつ timetable の整理のヒントを使用してこれを修正できます。xt は不等間隔サンプルで構いませんが、時間間隔の中央値と時間間隔の平均値は以下に従わなければならないという pspectrum の制約があります。

$$\frac{1}{100}<\frac{\text{Median time interval}}{\text{Mean time interval}}<100.$$

window — ウィンドウ時間分解能

正のスカラー

内部 pspectrum スペクトログラム計算のために使用するウィンドウ時間分解能。サンプル単位の正のスカラーとして指定します。window は既存のスペクトログラムを入力として使用する構文では必須、その他ではオプションです。関数 kurtogram を使用すると使用に最適なウィンドウ サイズを決定できます。pspectrum では既定の設定で 80% のオーバーラップを使用します。

s — 信号のスペクトログラムまたはパワー スペクトログラム

複素数行列 | 実数の非負の行列

信号のパワー スペクトログラムまたはスペクトル。行列 (スペクトログラム) または列ベクトル (スペクトル) として指定します。

• s が複素数の場合、pkurtosis は s を元の信号 (スペクトログラム) の短時間フーリエ変換 (STFT) として処理します。

• s が実数の場合、pkurtosis は s を元の信号 (パワー スペクトログラム) の STFT の絶対値の 2 乗として処理します。したがって、s のすべての要素は非負でなければなりません。

s を指定した場合、pkurtosis は独自のスペクトログラムまたはパワー スペクトログラムを生成する代わりに s を使用します。例については、カスタム スペクトログラムを使用したスペクトル尖度のプロットを参照してください。

データ型: single | double
複素数のサポート: あり

f — s の周波数

ベクトル

s が pkurtosis に明示的に与えられる場合のスペクトログラムまたはパワー スペクトログラム s の周波数。Hz 単位のベクトルとして指定します。f の長さは s の行数と等しくなければなりません。

'ConfidenceLevel', p — 信頼度

0.95 (既定値) | 範囲 [0, 1] の数値スカラー

信号がガウスおよび定常である可能性が高いかどうかを判断するために使用する信頼度。0 から 1 の数値スカラー値として指定します。p は、スペクトル尖度値がガウスおよび定常信号を示す thresh の範囲に影響します。したがって信頼度は、検出感度の調整パラメーターを提供します。この範囲外の尖度値は、(1-p) の確率で、非ガウスまたは非定常動作を示します。例については、異なる信頼度を使用した非定常信号のスペクトル尖度のプロットを参照してください。

出力引数

sk — スペクトル尖度

double ベクトル

スペクトル尖度。double ベクトルとして返されます。スペクトル尖度は、データが定常およびガウスである低値、および過渡が発生する高値を含む統計量です。スペクトル尖度の使い方の 1 つは、故障または劣化の結果として起こりうる非定常または非ガウス動作を検出して特定することです。高い値の尖度データは、このような信号成分を明らかにします。

fout — sk の周波数

double ベクトル

sk 値と関連付けられている周波数。Hz 単位のベクトルとして返されます。

thresh — 定常ガウス動作のスペクトル尖度帯のサイズ

スカラー

定常ガウス動作のスペクトル尖度帯域のサイズ。与えられた信頼度 p における、sk = 0 ラインを中心とする帯域の厚さを表す数値スカラーとして返されます。thresh で区切られた帯域外の偏位は、非定常または非ガウス動作を示す可能性があります。信頼度 p は、帯の厚さと結果の感度に直接影響します。例については、異なる信頼度を使用した非定常信号のスペクトル尖度のプロットを参照してください。

詳細

スペクトル尖度

スペクトル尖度 (SK) は、次をとることによって、周波数領域内の非定常または非ガウス動作を示して正確な位置を特定する統計ツールです。

• 定常ガウス ノイズのみが存在する周波数における小さい値

• 過渡が発生する周波数における高い正の値

この機能により、SK は回転機械システムにおける故障に関連した信号を検出および抽出するために強力なツールになります。SK は、それ自体で故障検出および分類のための特徴または条件インジケーターを特定できます。包絡線解析などの他のツールの前処理を行うことにより、SK は最適な帯域などのキー入力を供給できます[1]、[2]。

信号 x(t) のスペクトル尖度 K(f) は、信号の短時間フーリエ変換 (STFT) S(t,f) ベースで計算可能です。

$$S\left(t,f\right)={\displaystyle {\int }_{-\infty }^{\infty }x\left(\tau \right)w\left(\tau -t\right)e^{-j2\pi f\tau }d\tau },$$

ここで、w(t) は STFT で使用するウィンドウ関数です。K(f) は次のように計算されます。

$$K(f)=\frac{{\langle {\left|S(t,f)\right|}^4\rangle }_t}{{\langle {\left|S(t,f)\right|}^2\rangle }_t^2}-2,f\ne 0,$$

ここで、〈·〉_t は時間平均演算子です。

信号 x(t) が定常ガウス ノイズのみを含む場合、各周波数 f における K(f) は、0 平均値および分散 4/M の漸近的正規分布をもちます。ここで M は、S(t,f) における時間軸に沿った要素の数です。そのため、信頼度 α での統計的しきい値 s_α は、次のようになります。

$$s_{\alpha }={\Phi }^{-1}\left(\alpha \right)\frac{2}{\sqrt{M}},$$

ここで $${\Phi }^{-1}(\alpha )=\sqrt{2}{\mathrm{erf}}^{-1}(2\alpha -1)$$ は、標準正規分布の分位数関数です。

ここで重要な点は、STFT ウィンドウの長さ N_w によって周波数分解能 f_s/N_w (ここで f_s はサンプル レート) が直接決まることです。ウィンドウ サイズは、過渡インパルス間の間隔より短くなる必要がありますが、個々の過渡インパルスよりも長くなくてはなりません。

参照

[1] Antoni, J. "The Spectral Kurtosis: A Useful Tool for Characterising Non-Stationary Signals." Mechanical Systems and Signal Processing. Vol. 20, Issue 2, 2006, pp. 282–307.

[2] Antoni, J., and R. B. Randall. "The Spectral Kurtosis: Application to the Vibratory Surveillance and Diagnostics of Rotating Machines." Mechanical Systems and Signal Processing. Vol. 20, Issue 2, 2006, pp. 308–331.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

pkurtosis 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• 入力が純音信号である場合、結果はスペクトル尖度のインメモリ計算とわずかに数値が異なる場合があります。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2018a で導入

R2024b: pkurtosis は削除予定

pkurtosis 関数は将来のリリースで削除される予定です。代わりに spectralKurtosis を使用してください。spectralKurtosis を使用するには、コードを更新しなければなりません。

レート fs でサンプリングされた信号 x を考えます。

fs = 1000;
Ts = seconds(1/fs);
t = (0:1/fs:10)';

x = chirp(t,300,10,400);
xT = timetable(x,SampleRate=fs);

function y = wlen(x)
    wdiv = 2.^[1 3:7];
    y = ceil(x/wdiv(find(x < 2.^[6 11:14 Inf],1)));
end

wnd = 500;

[Sstft,Fstft] = stft(x,fs, ...
    FrequencyRange="onesided", ...
    Window=triang(600),FFTLength=1512,OverlapLength=421);

spectralKurtosis を使用してスペクトル尖度を取得するには、コードを次のように更新します。

R2024a 以前の元のコード	R2024b で更新されたコード
時間領域応答
sk = pkurtosis(xT);	fres = xT.Properties.SampleRate/winlen(height(xT)); [S,F] = pspectrum(xT,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=xT.Properties.SampleRate/2-fres) = 0;
sk = pkurtosis(x);	fres = 1/winlen(length(x)); [S,F] = pspectrum(x,1,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=1/2-fres) = 0;
sk = pkurtosis(x,fs);	fres = fs/winlen(length(x)); [S,F] = pspectrum(x,fs,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=fs/2-fres) = 0;
sk = pkurtosis(x,Ts);	fres = 1/(seconds(Ts)*winlen(length(x))); [S,F] = pspectrum(x,Ts,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=1/2/seconds(Ts)-fres) = 0;
sk = pkurtosis(x,t);	fres = 1/(mean(diff(t))*winlen(length(x))); [S,F] = pspectrum(x,t,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=1/2/mean(diff(t))-fres) = 0;
指定されたウィンドウ分解能での時間領域応答
sk = pkurtosis(xT,wnd);	fres = xT.Properties.SampleRate/wnd; [S,F] = pspectrum(xT,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=xT.Properties.SampleRate/2-fres) = 0;
sk = pkurtosis(x,[],wnd);	fres = 1/wnd; [S,F] = pspectrum(x,1,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=1/2-fres) = 0;
sk = pkurtosis(x,fs,wnd);	fres = fs/wnd; [S,F] = pspectrum(x,fs,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=fs/2-fres) = 0;
sk = pkurtosis(x,Ts,wnd);	fres = 1/(seconds(Ts)*wnd); [S,F] = pspectrum(x,Ts,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=1/seconds(Ts)/2-fres) = 0;
sk = pkurtosis(x,t,wnd);	fres = 1/(mean(diff(t))*wnd); [S,F] = pspectrum(x,t,"spectrogram", ... FrequencyResolution=fres, ... OverlapPercent=80); sK = spectralKurtosis(S,F,Scaled=false); sK(F<=fres|F>=1/mean(diff(t))/2-fres) = 0;
周波数領域応答
sk = pkurtosis(Sstft,fs,Fstft,wnd);	sK = spectralKurtosis(abs(Sstft).^2,Fstft, ... Scaled=false); sK(Fstft<=fs/wnd|Fstft>=fs*(1/2-1/wnd)) = 0;
sk = pkurtosis(Sstft,fs,Fstft,wnd);	sK = spectralKurtosis(x,fs, ... Window=triang(600),FFTLength=1512, ... OverlapLength=421,Scaled=false); sK(Fstft<=fs/wnd|Fstft>=fs*(1/2-1/wnd)) = 0;

• pkurtosis と同様に、spectralKurtosis で名前と値の引数 ConfidenceLevel を使用できます。

R2023b: コード生成での timetable の使用

関数 pkurtosis は、コード生成で MATLAB^® timetable をサポートします。

参考

kurtogram | pspectrum | spectralEntropy | spectralKurtosis

トピック

• 転動体ベアリングの故障診断 (Predictive Maintenance Toolbox)