uv2azel
Convert u/v coordinates to azimuth/elevation angles
Syntax
Description
AzEl = uv2azel(UV)
Examples
Find the corresponding azimuth/elevation representation for u = 0.5 and v = 0.
azel = uv2azel([0.5; 0])
azel = 2×1
30.0000
0
Input Arguments
Angle in u/v space, specified as a two-row matrix. Each column of the matrix represents a pair of coordinates in the form [u; v]. Each coordinate is between –1 and 1, inclusive. Also, each pair must satisfy u2 + v2≤ 1.
Data Types: double
Output Arguments
Azimuth and elevation angles, returned as a two-row matrix.
Each column of the matrix represents an angle in degrees, in the form
[azimuth; elevation]. The matrix dimensions of AzEl are
the same as those of UV.
More About
The u/v coordinates for the positive hemisphere x ≥ 0 can be derived from the phi and theta angles.
The relation between the two coordinates is
In these expressions, φ and θ are the phi and theta angles, respectively.
To convert azimuth and elevation to u and v use the transformation
which is valid only in the range abs(az)≤=90.
The values of u and v satisfy the inequalities
Conversely, the phi and theta angles can be written in terms of u and v using
The azimuth and elevation angles can also be written in terms of u and v:
The phi angle (φ) is the angle from the positive y-axis to the vector’s orthogonal projection onto the yz plane. The angle is positive toward the positive z-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the x-axis to the vector itself. The angle is positive toward the yz plane. The theta angle is between 0 and 180 degrees.
The figure illustrates phi and theta for a vector that appears as a green solid line.

The coordinate transformations between φ/θ and az/el are described by the following equations
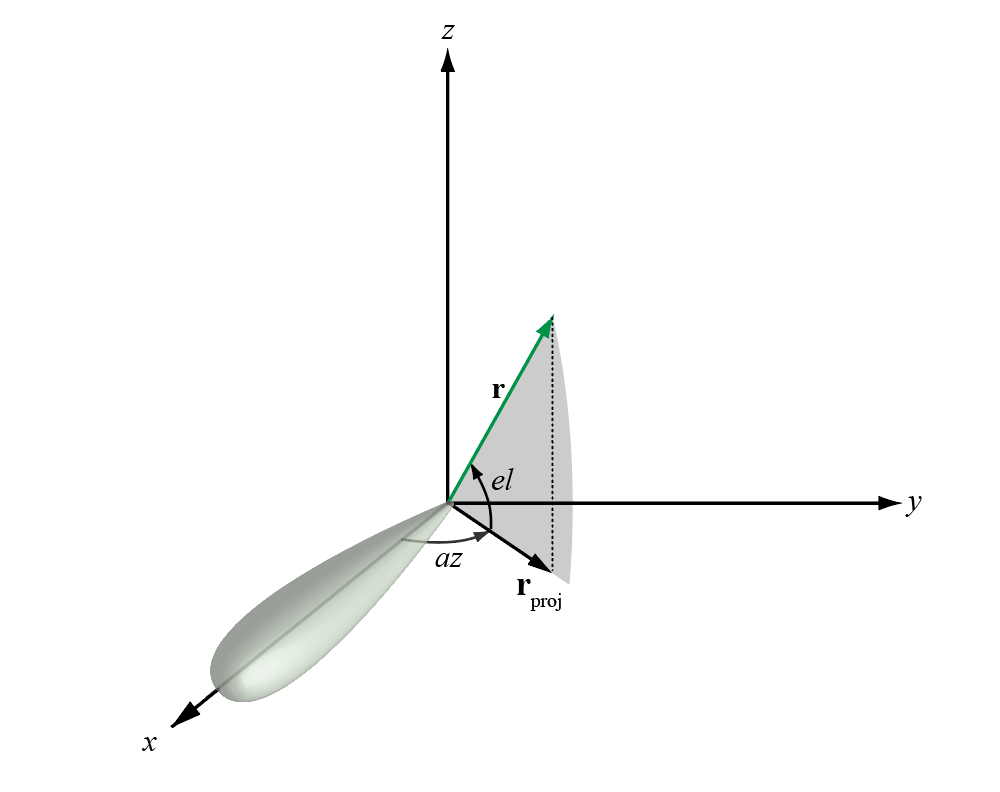
The azimuth angle of a vector is the angle between the x-axis and the orthogonal projection of the vector onto the xy plane. The angle is positive in going from the x axis toward the y axis. Azimuth angles lie between –180 and 180 degrees. The elevation angle is the angle between the vector and its orthogonal projection onto the xy-plane. The angle is positive when going toward the positive z-axis from the xy plane. By default, the boresight direction of an element or array is aligned with the positive x-axis. The boresight direction is the direction of the main lobe of an element or array.
Note
The elevation angle is sometimes defined in the literature as the angle a vector makes with the positive z-axis. The MATLAB® and Phased Array System Toolbox™ products do not use this definition.
This figure illustrates the azimuth angle and elevation angle for a vector shown as a green solid line.
Extended Capabilities
Usage notes and limitations:
Does not support variable-size inputs.
Version History
Introduced in R2012a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)