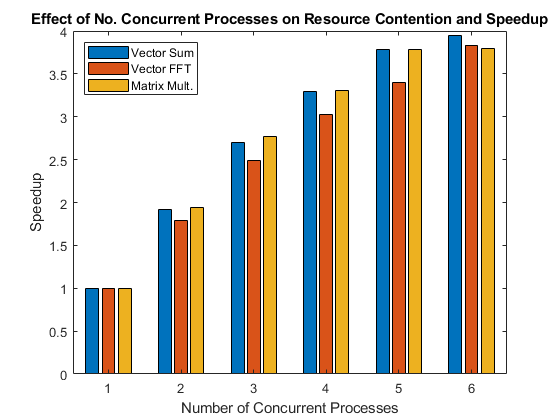
リソース競合と効率性に関する例

なぜ、このようなシンプルなベンチマークを実行することに意義があるのかを理解するため、次の例について考えてみてください。1 人の人がバケツに水を満たし、少し離れた場所まで運び、空にして、元の場所に戻って再び水を満たすという工程が 1 分で行われる場合、2 人でそれぞれ 1 つのバケツを使用して同じ工程を行うとすると、どのくらいの時間がかかるでしょうか。このシンプルな例えは、この例で説明するタスク並列処理のベンチマークを非常によく表しています。最初の印象では、2 人が同時に同じことを行うと 1 人の場合に比べて効率性が低下して非合理的になるように思えます。

1 本のパイプをめぐる競合: リソース競合

前述の例で何も問題なく作業が行われた場合、2 人は バケツ 1 杯の水を運ぶ一連の工程をそれぞれ 1 分で完了させます。各人が 1 つのバケツを速やかに満たして目的の場所まで運び、空にして戻り、お互いの作業を決して妨げないようにします。

しかし、バケツの水は 1 本の細いホースを使用して満たさなければならないという状況を想像してみてください。2 人が同時にホースにたどりつくと、1 人は待たなければなりません。これは、共有リソースの競合の一例です。おそらく 2 人であれば同時にホースを使用しなくても済むため、このホース 1 本でニーズを満たしているかもしれません。しかし、10 人がそれぞれ 1 つのバケツで水を運ぶ場合は、誰かが必ず待たなければならなくなるでしょう。

この例えでは、ホースがコンピューターのハードウェア (さらに具体的に言うと、メモリ) に相当します。複数のプログラムが 1 つの CPU コアでそれぞれ同時に実行され、それらすべてがコンピューターのメモリに格納されているデータにアクセスする必要がある場合、メモリ帯域幅が限られるため、いくつかのプログラムが待機しなければならなくなることもあります。

同じホース、異なる距離、異なる結果

2 人がそれぞれ 1 つのバケツを運ぶときにホースで競合が発生し、その場合はタスクが変わり、少し遠くまで水を運ばなければならないとします。この変更されたタスクを実行する場合、2 人は時間の大部分を作業 (つまり、バケツの運搬) に費やし、共有リソース (つまり、ホース) の競合の時間はわずかになります。そのため、同時にホースが必要になる可能性は低くなり、したがって、変更されたタスクでは並列処理効率が元のタスクに比べて高くなります。

以上のことをこの例のベンチマークに当てはめると、プログラムの実行ではコンピューター メモリへの多数のアクセスが必要でも、データが取得されると、それを使用して実行する処理の量は非常に少ないということになります。一方で、プログラムで取得したデータを使用して多量の計算を実行する場合は、データの取得にどのくらいの時間がかかるかということは重要ではなくなり、メモリ アクセス待機時間は計算時間に比べてわずかなものとなります。

また、アルゴリズムのメモリ アクセスがどの程度予測可能かということもメモリ アクセス競合の度合いに影響します。メモリが規則的かつ予測可能な方法でアクセスされる場合は、メモリが不規則にアクセスされる場合よりも競合が少なくなります。この件については、特異値分解の計算の方が行列の乗算よりも競合が発生しやすい例などを使用して後述します。

並列プールの起動

既存の並列プールをすべて閉じ、parpoolを使用してプロセスベースの並列プールを起動します。既定の基本設定を使用すると、parpool はローカル マシン上で 1 つの物理 CPU コアにつき 1 つのワーカーをもつプール (上限は推奨ワーカー数) を起動します。

delete(gcp("nocreate")); % Close any existing parallel pools
p = parpool("Processes");

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to the parallel pool (number of workers: 6).

poolSize = p.NumWorkers;

時間測定関数

この例の最後に時間測定関数 timingFcn を示しています。この時間測定関数は、spmdステートメント内で関数を 5 回実行し、同時実行の特定のレベルについて観測される最小実行時間を保持します。

前に述べたように、この例のベンチマークの対象はタスク並列処理の問題であるため、実際の実行時間のみを測定します。つまり、この例では MATLAB®、Parallel Computing Toolbox™、または spmd 言語構成のパフォーマンスのベンチマークは実行しません。代わりに、この例ではプログラムの複数のコピーを同時に実行するための OS とハードウェアの性能のベンチマークを実行します。

ベンチマークの問題を用意

処理のたびにコンピューターのメモリから CPU に取得しなければならないような大きなサイズの入力行列を作成します。つまり、リソース競合が発生する十分な大きさにします。

sz = 2048;
m = rand(sz*sz,1);

総和演算

この例の最後に、単一の配列に対して反復的な総和計算を実行する関数 sumOp を示しています。総和演算は計算が軽量であるため、この関数の複数のコピーを大きな入力配列で同時に実行するとリソース競合が発生すると想定されます。その結果、複数の計算の評価を同時に行う場合は、これらの評価を同時に行わなければアイドル状態になる CPU で計算の評価を 1 回だけ実行する場合よりも、総和関数の評価にかかる時間は長くなることが予測されます。

高速フーリエ変換演算

この例の最後に、ベクトルに対して反復的な高速フーリエ変換 (FFT) を実行する関数 fftOp を示しています。FFT 演算は総和演算よりも多くの計算を必要とするので、複数の FFT 関数呼び出しを同時に評価する場合のパフォーマンスの低下は総和関数の呼び出しとは異なるものになると予測されます。

行列乗算演算

この例の最後に、行列乗算を実行する関数 multOp を示しています。行列乗算の場合はメモリ アクセスが極めて規則的であるため、この演算はマルチコア マシンで非常に効率的に並列実行できる可能性があります。

リソース競合に関する検証

N の値を 1 から並列プールのサイズまでとして、N 個の総和関数を N 個のワーカーで同時に評価するのに要する時間を測定します。

tsum = timingFcn(@() sumOp(m), 1:poolSize);

Execution times: 0.279930, 0.292188, 0.311675, 0.339938, 0.370064, 0.425983

N の値を 1 から並列プールのサイズまでとして、N 個の FFT 関数を N 個のワーカーで同時に評価するのに要する時間を測定します。

tfft = timingFcn(@() fftOp(m),1:poolSize);

Execution times: 0.818498, 0.915932, 0.987967, 1.083160, 1.205024, 1.280371

N の値を 1 から並列プールのサイズまでとして、N 個の行列乗算関数を N 個のワーカーで同時に評価するのに要する時間を測定します。

m = reshape(m,sz,sz);
tmtimes = timingFcn(@() multOp(m),1:poolSize);

Execution times: 0.219166, 0.225956, 0.237215, 0.264970, 0.289410, 0.346732

clear m

時間測定結果を 1 つの配列に結合し、複数の関数呼び出しを同時に実行することによって実現される高速化を計算します。

allTimes = [tsum(:), tfft(:), tmtimes(:)];
speedup = (allTimes(1,:)./allTimes).*((1:poolSize)');

結果を棒グラフにプロットします。このグラフは "ウィーク スケーリング" と呼ばれる方法による高速化を示します。ウィーク スケーリングでは、プロセスまたはプロセッサの数を変えますが、各プロセスまたはプロセッサにおける問題の規模は固定します。そのようにしてプロセスまたはプロセッサの数を増やしながら、問題の全体的な規模が大きくなるようにします。一方、ストロング スケーリングでは、問題の規模は固定し、プロセスまたはプロセッサの数を変えます。このようにすると、プロセスまたはプロセッサの数が増加するにつれて、各プロセスまたはプロセッサで実行される処理は少なくなります。

bar(speedup)
legend('Vector Sum', 'Vector FFT', 'Matrix Mult.', ...
    'Location', 'NorthWest')
xlabel('Number of Concurrent Processes');
ylabel('Speedup')
title(['Effect of No. Concurrent Processes on ', ...
    'Resource Contention and Speedup']);

実際のアプリケーションにおける影響

上記のグラフから、問題の規模は同じコンピューターでも変化することがわかります。問題やコンピューターによって動作がまったく異なるものになるという事実を考慮すると、「(並列) アプリケーションのパフォーマンスがマルチコア マシンまたはクラスターでどの程度のものになるか」という質問に対する一般的な回答を提示するのがなぜ不可能であるかが明らかになります。つまり、この質問に対する回答は対象のアプリケーションとハードウェアによって真に異なるためです。

リソース競合に対するデータ サイズの影響の測定

リソース競合は、実行する関数だけでなく、処理するデータのサイズにも影響されます。これについて説明するため、さまざまなサイズの入力データを使用するいくつかの関数の実行時間を測定します。これまでと同様、MATLAB やそのアルゴリズムではなく、これらの計算を同時に実行するハードウェアの性能のベンチマークを実行します。さまざまなデータ サイズによる影響に加え、異なるメモリ アクセス パターンの影響も調査できるようにするため、これまでよりも多くの関数について考えます。前述の関数に加え、ベンチマークの実行に以下も使用します。

データ サイズを定義し、テストで使用する演算を指定します。

szs = [128, 256, 512, 1024, 2048];
operations = {'Vector Sum', 'Vector FFT', 'Matrix Mult.', 'Matrix LU', ...
    'Matrix SVD', 'Matrix EIG'};

それぞれのデータ サイズと関数をループ処理し、逐次実行した場合の時間と並列プールのすべてのワーカーで同時に実行した場合の時間を測定します。

speedup = zeros(length(szs), length(operations));

% Loop over the data sizes
for i = 1:length(szs)
    sz = szs(i);
    fprintf('Using matrices of size %d-by-%d.\n', sz, sz);
    j = 1;

    % Loop over the different operations
    for f = [{@sumOp; sz^2; 1}, {@fftOp; sz^2; 1}, {@multOp; sz; sz}, ...
            {@lu; sz; sz}, {@svd;  sz; sz}, {@eig;  sz; sz}]
        op = f{1};
        nrows = f{2};
        ncols = f{3};
        m = rand(nrows, ncols);
        % Compare sequential execution to execution on all workers
        tcurr = timingFcn(@() op(m), [1, poolSize]);
        speedup(i, j) = tcurr(1)/tcurr(2)*poolSize;
        j = j + 1;
    end

end

Using matrices of size 128-by-128.

Execution times: 0.000496, 0.000681
Execution times: 0.001933, 0.003149
Execution times: 0.000057, 0.000129
Execution times: 0.000125, 0.000315
Execution times: 0.000885, 0.001373
Execution times: 0.004683, 0.007004

Using matrices of size 256-by-256.

Execution times: 0.001754, 0.002374
Execution times: 0.012112, 0.022556
Execution times: 0.000406, 0.001121
Execution times: 0.000483, 0.001011
Execution times: 0.004097, 0.005329
Execution times: 0.023690, 0.033705

Using matrices of size 512-by-512.

Execution times: 0.008338, 0.018826
Execution times: 0.046627, 0.089895
Execution times: 0.003986, 0.007924
Execution times: 0.003566, 0.007190
Execution times: 0.040086, 0.081230
Execution times: 0.185437, 0.261263

Using matrices of size 1024-by-1024.

Execution times: 0.052518, 0.096353
Execution times: 0.235325, 0.339011
Execution times: 0.030236, 0.039486
Execution times: 0.022886, 0.048219
Execution times: 0.341354, 0.792010
Execution times: 0.714309, 1.146659

Using matrices of size 2048-by-2048.

Execution times: 0.290942, 0.407355
Execution times: 0.855275, 1.266367
Execution times: 0.213512, 0.354477
Execution times: 0.149325, 0.223728
Execution times: 3.922412, 7.140040
Execution times: 4.684580, 7.150495

それぞれのデータ サイズについて、各演算をプールのすべてのワーカーで同時に実行した場合の高速化をプロットします。これは、理想的な高速化を示します。

figure
ax = axes;
plot(speedup)
set(ax.Children, {'Marker'}, {'+', 'o', '*', 'x', 's', 'd'}')
hold on

plot([1 length(szs)],[poolSize poolSize], '--')

xticks(1:length(szs));
xticklabels(szs + "^2")
xlabel('Number of Elements per Process')

ylim([0 poolSize+0.5])
ylabel('Speedup')

legend([operations, {'Ideal Speedup'}], 'Location', 'SouthWest')
title('Effect of Data Size on Resource Contention and Speedup')

hold off

結果を確認するときには、関数でどのようにデータが CPU のキャッシュとやり取りされるかということに留意してください。データ サイズが小さい場合は、すべての関数で CPU キャッシュが常に使用されます。その場合、良好な高速化を実現できることが予測できます。入力データが CPU キャッシュに対して大きすぎると、メモリ アクセスの競合によるパフォーマンスの低下が見られるようになります。

サポート関数

時間測定関数

関数 timingFcn は、関数ハンドルと同時実行プロセス数を受け取ります。この関数は、同時実行プロセス数を N として、関数ハンドルで表される関数を N 個の並列ワーカーを使用して spmd ブロック内で N 回実行する場合の実行時間を測定します。

function time = timingFcn(fcn, numConcurrent)

time = zeros(1,length(numConcurrent));
numTests = 5;

% Record the execution time on 1 to numConcurrent workers
for ind = 1:length(numConcurrent)
    n = numConcurrent(ind);

    spmd(n)
        tconcurrent = inf;

        % Time the function numTests times, and record the minimum time
        for itr = 1:numTests
            % Measure only task parallel runtime
            spmdBarrier;
            tic;
            fcn();
            % Record the time for all to complete
            tAllDone = spmdReduce(@max, toc);  
            tconcurrent = min(tconcurrent, tAllDone);
        end
        
    end

    time(ind) = tconcurrent{1};
    clear tconcurrent itr tAllDone
    if ind == 1
        fprintf('Execution times: %f', time(ind));
    else
        fprintf(', %f', time(ind));
    end
end

fprintf('\n');
end

総和関数

関数 sumOp は、入力行列に対して総和演算を 100 回実行し、結果を累積します。総和演算は、正確な時間測定を得るために 100 回実行されます。

function sumOp(m)
s = 0;

for itr = 1:100
    s = s + sum(m);
end

end

FFT 関数

関数 fftOp は、入力配列に対して FFT 演算を 10 回実行します。FFT 演算は、正確な時間測定を得るために 10 回実行されます。

function fftOp(m)

for itr = 1:10
    fft(m);
end

end

行列乗算関数

関数 multOp は、入力行列にそれ自身を乗算します。

function multOp(m)
m*m;
end