錐計画法を使用した区分線形ばね質量系のエネルギーの最小化、問題ベース

この例では、問題ベースのアプローチを使用して、2 つの固定点からぶら下がっているばね質量系の平衡位置を見つける方法を示します。ばねには区分線形張力がかかります。系は、2 つの次元の $$n$$ 個の質量で構成されます。質量 $$i$$ はばね $$i$$ とばね $$i+1$$ に接続されます。ばね $$1$$ とばね $$n+1$$ は別々の固定点に接続されます。この場合、ばね $$i$$ の 0 力長さは正の長さ $$l(i)$$ で、ばねは長さ $$q+l(i)$$ に伸びたときに力 $$k(i)q$$ を発生させます。問題は、質量の最小位置エネルギー構成を見つけることです。ここで、位置エネルギーは、重力と非線形ばねの伸びから生じます。平衡は、最小エネルギー構成で実現します。

この図は、2 つの固定点からつるされている 5 つのばねと 4 つの質量を示しています。

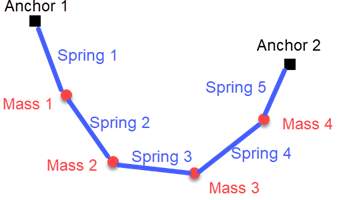
高さ $$h$$ における質量 $$m$$ の位置エネルギーは $$mgh$$ です。ここで、$$g$$ は地球上の重力定数です。また、長さ $$q$$ に伸びた、ばね定数 $$k$$ の理想的な線形ばねの位置エネルギーは $$k{q}^2/2$$ です。現在のモデルは、ばねが理想的ではありませんが、非ゼロの静止長 $$l$$ をもちます。

この例の数学的基礎は、Lobo、Vandenberghe、Boyd、および Lebret [1] にあります。この例のソルバーベースのバージョンについては、錐計画法を使用した区分線形ばね質量系のエネルギーの最小化 (ソルバーベース)を参照してください。

数学的定式化

質量 $$i$$ の位置は、水平座標が $$x_1(i)$$ で、垂直座標が $$x_2(i)$$ の $$x(i)$$ です。質量 $$i$$ は、$$gm(i)x_2(i)$$ の重力による位置エネルギーをもちます。ばね $$i$$ の位置エネルギーは $$k(i)(d(i)-l(i){)}^2/2$$ です。ここで、$$d(i)$$ は、質量 $$i$$ と質量 $$i-1$$ 間のばねの長さです。固定点 1 を質量 0 の位置として、固定点 2 を質量 $$n+1$$ の位置としてとります。前述のエネルギー計算は、ばね $$i$$ の位置エネルギーが以下であることを示しています。

$$Energy(i)=\frac{k(i)(\Vert x(i)-x(i-1)\Vert -l(i){)}^2}{2}$$.

この位置エネルギー問題を 2 次錐計画法の問題として再定式化するには、Lobo [1] で説明されているように、いくつかの新しい変数の導入が必要です。項 $$Energy(i)$$ の平方根に等しい変数 $$t(i)$$ を作成します。

$$t(i)=\sqrt{\frac{k(i)(\Vert x(i)-x(i-1)\Vert -l(i){)}^2}{2}}.$$

$$e$$ を単位列ベクトル $$\left[\genfrac{}{}{0ex}{}{0}{1}\right]$$ とします。すると、$$x_2(i)=e^{T}x(i)$$ になります。問題は次のようになります。

$$\underset{x,t}{\min }(\sum _{i}gm(i)e^{T}x(i)+\Vert t{\Vert }^2).$$ (1)

ここで、$$t$$ を、$$t(i)$$ の以前の方程式で与えるのではなく、自由ベクトル変数と見なします。$$x(i)$$ と $$t(i)$$ の関係を次の錐制約の新しいセットに組み込みます。

$$\Vert x(i)-x(i-1)\Vert -l(i)\le \sqrt{\frac{2}{k(i)}}t(i).$$ (2)

目的関数は、まだ、coneprog に規定されているように、変数内で線形ではありません。新しいスカラー変数 $$y$$ を導入します。不等式 $$\Vert t{\Vert }^2\le y$$ は次の不等式と同等であることに注意してください。

$$\Vert \left[\genfrac{}{}{0ex}{}{2t}{1-y}\right]\Vert \le 1+y$$.(3)

ここで、問題は、次を最小化することです。

$$\underset{x,t,y}{\min }(\sum _{i}gm(i)e^{T}x(i)+y)$$ (4)

これは、(2) に記載されている $$x(i)$$ と $$t(i)$$ に対する錐制約と追加の錐制約 (3) の影響を受けます。錐制約 (3) は $$\Vert t{\Vert }^2\le y$$ であることを確保します。したがって、問題 (4) は問題 (1) と同等です。

問題 (4) の目的関数と錐制約は coneprog を使用した解法に適しています。

MATLAB® での定式化

6 つのばね制約 $$k$$、6 つの長さ制約 $$l$$、および 5 つの質量 $$m$$ を定義します。

k = 40*(1:6);
l = [1 1/2 1 2 1 1/2];
m = [2 1 3 2 1];
g = 9.807;

数学的問題の変数に対応する最適化変数を定義します。簡単にするため、固定点を 2 つの仮想質点 x(1,:) および x(end,:) として設定します。この定式化により、各ばねは 2 つの質量間で伸縮することになります。

nmass = length(m) + 2;
% k and l have nmass-1 elements
% m has nmass - 2 elements
x = optimvar('x',[nmass,2]);
t = optimvar('t',nmass-1,'LowerBound',0);
y = optimvar('y','LowerBound',0);

最適化問題を作成し、目的関数を (4) の式に設定します。

prob = optimproblem;
obj = dot(x(2:(end-1),2),m)*g + y;
prob.Objective = obj;

式 (2) に相当する錐制約を作成します。

conecons = optimineq(nmass - 1);
for ii = 1:(nmass-1)
    conecons(ii) = norm(x(ii+1,:) - x(ii,:)) - l(ii) <= sqrt(2/k(ii))*t(ii);
end
prob.Constraints.conecons = conecons;

固定点 anchor0 および anchorn を指定します。2 つの仮想先端質量が固定点にあることを指定する等式制約を作成します。

anchor0 = [0 5];
anchorn = [5 4];
anchorcons = optimeq(2,2);
anchorcons(1,:) = x(1,:) == anchor0;
anchorcons(2,:) = x(end,:) == anchorn;
prob.Constraints.anchorcons = anchorcons;

式 (3) に相当する錐制約を作成します。

ycone = norm([2*t;(1-y)]) <= 1 + y;
prob.Constraints.ycone = ycone;

問題を解く

問題の定式化は完了です。solve を呼び出して問題を解きます。

[sol,fval,eflag,output] = solve(prob);

Solving problem using coneprog.
Optimal solution found.

解の点とアンカーをプロットします。

plot(sol.x(2:(nmass-1),1),sol.x(2:(nmass-1),2),'ro')
hold on
plot([sol.x(1,1),sol.x(end,1)],[sol.x(1,2),sol.x(end,2)],'ks')
plot(sol.x(:,1),sol.x(:,2),'b--')
legend('Calculated points','Anchor points','Springs','Location',"best")
xlim([sol.x(1,1)-0.5,sol.x(end,1)+0.5])
ylim([min(sol.x(:,2))-0.5,max(sol.x(:,2))+0.5])
hold off

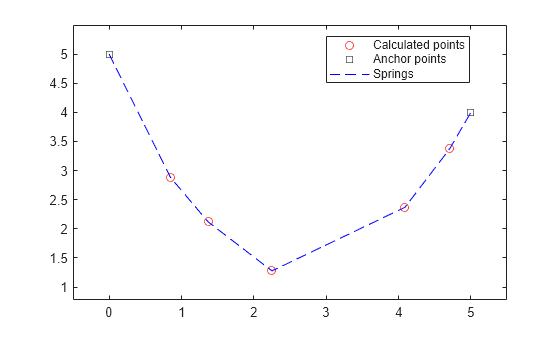
パラメーターの m、l、および k の値を変更して、それらがどのように解に影響するかを確認します。質量の数を変更することもできます。コードは、入力されたデータから質量の数を抽出します。

参考文献

[1] Lobo, Miguel Sousa, Lieven Vandenberghe, Stephen Boyd, and Hervé Lebret.“Applications of Second-Order Cone Programming.”Linear Algebra and Its Applications 284, no. 1–3 (November 1998):193–228. https://doi.org/10.1016/S0024-3795(98)10032-0.

参考

coneprog

関連するトピック

• 錐計画法を使用した区分線形ばね質量系のエネルギーの最小化 (ソルバーベース)
• 問題ベースの最適化の設定
• 問題ベースの錐計画法の制約の記述