グリーン水素製造システムの最適化
この例では、電解槽から水素を生成するためのグリーン システムの主要コンポーネントのサイズを決定する方法を示します。主要コンポーネントは次のとおりです。
太陽電池アレイ
風力タービン
バッテリー システム
電力グリッドへの双方向接続
水素 (H2) を生成するための電解槽
電気負荷
次の図は、さまざまなコンポーネントがどのように電気的に接続されるかを示しています。
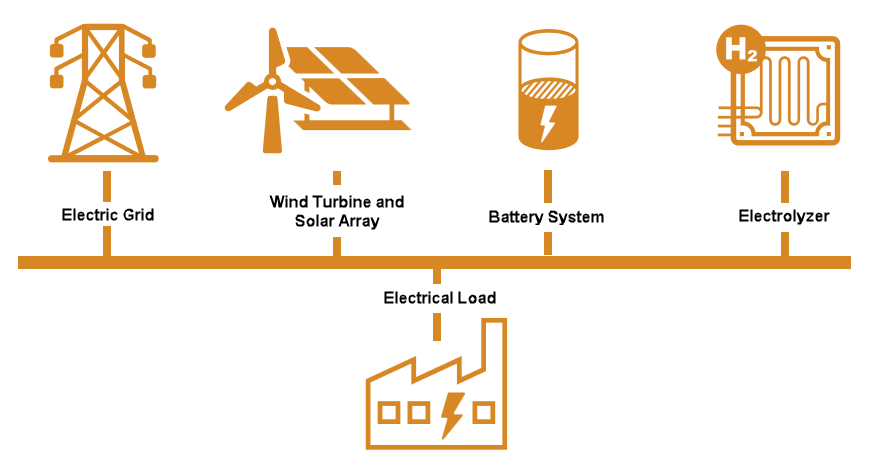
最適なコンポーネント サイズを決定するには、技術経済性分析を使用します。技術的な考慮事項には、グリーン水素製造システムの物理的な動作制約が含まれます。正味現在価値 (NPV) を使用して、システムへの投資の採算性を評価します。割引率は 5% であると仮定します。この例の後半では、割引率が異なる場合の影響を確認できます。
問題のデータ
以下についての 20 年間にわたる 1 時間ごとのデータで構成されるデータ セットを読み込みます。
負荷電力 (kW)
グリッド電力の価格 ($/kW)
太陽プロファイル ([0 1] に正規化)
風プロファイル ([0 1] に正規化)
グリーン水素の価格 ($/kg)
実際には、このタイプのデータは公開データ ソースや内部データ ソース、または予測モデルや予想モデルから得られます。この例では、代表的な合成データを単一のデータ構造体に読み込みます (便宜上)。
loadPower = load("loadPower.mat"); priceGrid = load("priceGrid.mat"); priceH2 = load("priceH2.mat"); solarProfile = load("solarProfile.mat"); windProfile = load("windProfile.mat"); data = struct(loadPower=loadPower.loadPower,... priceGrid=priceGrid.priceGrid,... priceH2=priceH2.priceH2,... solarProfile=solarProfile.solarProfile,... windProfile=windProfile.windProfile); clear loadPower priceGrid priceH2 solarProfile windProfile numYears = 20; numSteps = 24*365*numYears; % Ignore the effects of leap years and seconds. timeStep = 1; % unit = hours. Convert from power to energy by multiplying by timeStep.
NPV の計算では、年間割引率は 5% であると仮定します。
discount_rate = 0.05;
電力の消費量と生産量のモデル化
システムの各コンポーネントをモデル化します。まず、最大化を目的とする最適化問題を作成します。ここで、目的関数は NPV です (後ほどこの例で指定します)。
H2productionProblem = optimproblem(ObjectiveSense="maximize");すべての変数を連続変数として扱います。
グリッドの電力
グリッドの電力使用量を表す gridPower という名前の最適化変数ベクトルを作成します。
システムではグリッドから最大 100 kW の電力を使用でき、グリッドに最大 10 kW の電力を供給することもできると仮定します。そのため、システムではグリッドからの電力の購入とグリッドへの電力の売却を両方行うことができます。
価格は、グリッドからの電力の購入とグリッドへの電力の売却で同じであると仮定します。
gridPowerBuyLimit = 100; % kW gridPowerSellLimit = -10; % kW - negative value to indicate selling back to grid gridPower = optimvar("gridPower",numSteps,... LowerBound=gridPowerSellLimit,UpperBound=gridPowerBuyLimit);
太陽光発電
太陽光発電の容量を表す solarRating という名前の最適化変数ベクトルを作成します。
最大電力が
solarRatingの単一の太陽光発電ユニットを仮定します。ここで、solarRatingは 500 kW 以下の最適化変数です。1 時間ごとの太陽光発電量は
data.solarProfile*solarRatingです。太陽光発電ユニットのコストはその定格に正比例します。
solarPowerCost = 1500; % $/kW of capacity, so total cost = solarPowerCost*solarRating.太陽光発電ユニットのコストは https://atb.nrel.gov/electricity/2021/residential_pv から取得されます。
maxSolarRating = 500; % kW solarRating = optimvar("solarRating",LowerBound=0,UpperBound=maxSolarRating);
風力発電
風力発電の容量を表す windRating という名前の最適化変数ベクトルを作成します。
最大電力が
windRatingの単一の風力発電ユニットを仮定します。ここで、windRatingは 500 kW 以下の最適化変数です。1 時間ごとの風力発電量は
data.windProfile*windRatingです。風力発電ユニットのコストはその定格に正比例します。
windPowerCost = 1500; % $/kW of capacity, so total cost = windPowerCost*windRating. maxWindRating = 500; % kW windRating = optimvar("windRating",LowerBound=0,UpperBound=maxWindRating);
蓄電
電力容量 (蓄電池に出入りする時間単位あたりのエネルギー) と合計エネルギー容量の両方をモデル化します。
電力容量が
storagePowerRating(200 kW 以下の最適化変数) であると仮定します。最大エネルギー容量が
storageEnergyRating(10,000 kWh 以下の最適化変数) の単一の蓄電ユニットを仮定します。
蓄電ユニットのコストは次の 3 つの部分で構成されます。
固定コスト $5982
電力容量の kW あたりのコスト $1690
エネルギー容量の kWh あたりのコスト $354
これらのコストは https://atb.nrel.gov/electricity/2021/residential_battery_storage から取得されます。
storageFixedCost = 5982; % $ one-time cost storagePowerCost = 1690; % $/kW storageEnergyCost = 354; % $/kWh
蓄電ユニットの最適化変数を作成します。storagePower を各タイム ステップでの電力を表すベクトルとして作成し、storageEnergy を各タイム ステップでのエネルギーを表すベクトルとして作成します。また、それぞれ電力とエネルギーの容量を表すスカラー変数 storagePowerRating および storageEnergyRating を作成します。
maxStoragePowerRating = 200; % kW maxStorageEnergyRating = 10e3; % kWh storagePower = optimvar("storagePower",numSteps,... LowerBound=-maxStoragePowerRating,UpperBound=maxStoragePowerRating); storageEnergy = optimvar("storageEnergy",numSteps,... LowerBound=0,UpperBound=maxStorageEnergyRating); storagePowerRating = optimvar("storagePowerRating",LowerBound=0,UpperBound=maxStoragePowerRating); storageEnergyRating = optimvar("storageEnergyRating",LowerBound=0,UpperBound=maxStorageEnergyRating);
電力変数とエネルギー変数にはエネルギー バランスの関係があります。1 時間に使用されるか得られる電力により、蓄積されるエネルギーが増減します。このエネルギー バランスを適用するには、最適化制約を作成します。
storageEnergyBalance = optimconstr(numSteps); % Initialize storageEnergyBalance(1) = storageEnergy(1) == -storagePower(1)*timeStep; % Initialize assuming zero stored energy at first storageEnergyBalance(2:numSteps) = storageEnergy(2:numSteps) == ... storageEnergy(1:numSteps-1) - storagePower(2:numSteps)*timeStep; H2productionProblem.Constraints.storageEnergyBalance = storageEnergyBalance;
蓄電システムは時間の経過とともに徐々に劣化します。蓄電容量と電力限界の両方について、蓄電システムの劣化をシステムの寿命にわたって 5% の線形劣化でモデル化します。
degradationFactor = linspace(1,1-0.05,numSteps)'; H2productionProblem.Constraints.chargeUpper = ... storageEnergy <= storageEnergyRating*degradationFactor; H2productionProblem.Constraints.storagePowerLower1 = ... storagePower >= -storagePowerRating*degradationFactor; H2productionProblem.Constraints.storagePowerUpper = ... storagePower <= storagePowerRating*degradationFactor;
蓄電池の電力について、風力発電または太陽光発電のみを使用してグリッドからのエネルギーは使用しないように制約します。この制約により、蓄電ユニットが水素の生成中に再生可能資源からのエネルギーのみを確実に供給するようになります。
renewablePower = data.solarProfile*solarRating + data.windProfile*windRating; H2productionProblem.Constraints.storagePowerLower2 = storagePower >= -renewablePower;
電解槽ユニット
電解槽が 1 時間ごとに使用する電力を表す electrolyzerPower という名前の最適化変数と、electrolyzerPower の最大値を表す electrolyzerPowerRating という名前の最適化変数を作成します。
単一の電解槽ユニットを仮定します。
電解槽の電力定格は 0 ~ 50 kW の範囲です。
電解槽は水素を継続的に生成し、蓄積された水素を週に 1 回売却します。
水素をシステムに蓄積するためのコストは考慮されません。
電解槽は 55 kWh のエネルギーを使用して 1 kg の水素を生成します。
電解槽ユニットのコストはその電力容量に比例します。
electrolyzerPowerCost = 4000; % $/kW of capacity, so total cost = electrolyzerPowerCost*electrolyzerPowerRating.電解槽パラメーターの変数を作成します。
maxElectrolyzerPowerRating = 50; % kW H2SellInterval = 24*7; % hours in one week H2ProdEnergy = 55; % kWh/kg
電解槽の電力とタイム ステップごとに蓄積される水素の両方の最適化変数を作成します。
electrolyzerPower = optimvar("electrolyzerPower",numSteps,... LowerBound=0,UpperBound=maxElectrolyzerPowerRating); electrolyzerPowerRating = optimvar("electrolyzerPowerRating",LowerBound=0,UpperBound=maxElectrolyzerPowerRating); H2_stored = optimvar("H2_stored",numSteps,LowerBound=0,UpperBound=1e12);
電解槽の電力を使用して水素を生成するように強制する制約を作成します。
electrolyzerH2prod = optimconstr(numSteps);
electrolyzerH2prod(1) = H2_stored(1) == electrolyzerPower(1)*timeStep/H2ProdEnergy;
electrolyzerH2prod(2:numSteps) = H2_stored(2:numSteps) == ...
H2_stored(1:numSteps-1) + electrolyzerPower(2:numSteps)*timeStep/H2ProdEnergy;
H2productionProblem.Constraints.electrolyzerH2prod = electrolyzerH2prod;生成されたすべての水素が指定の間隔で売却されるようにする制約を作成します。
H2productionProblem.Constraints.electrolyzerH2prod(H2SellInterval+1:H2SellInterval:numSteps) = ... H2_stored(H2SellInterval+1:H2SellInterval:numSteps) == ... electrolyzerPower(H2SellInterval+1:H2SellInterval:numSteps)*timeStep/H2ProdEnergy;
指定の売却間隔で売却される水素量を計算します。
H2_sold = H2_stored(H2SellInterval:H2SellInterval:numSteps);
電解槽の電力を maxElectrolyzerPowerRating に制約し、蓄電ユニットの電力容量とエネルギー容量の場合と同じ劣化係数を使用して経時的な線形劣化を表します。
H2productionProblem.Constraints.electrolyzerPowerUpper1 = ...
electrolyzerPower <= electrolyzerPowerRating*degradationFactor;電解槽に太陽光発電、風力発電、および蓄電池の電力のみが供給され、グリッドの電力は供給されないように制約します。この制約により、水素が確実に再生可能資源のみで生成されるようになります。
H2productionProblem.Constraints.electrolyzerPowerUpper2 = ...
electrolyzerPower <= renewablePower + storagePower;システムの電力平衡
使用電力と電解槽の電力の和がその他の電力コンポーネントの合計と等しいという制約を作成します。
H2productionProblem.Constraints.powerBalance = ... data.loadPower + electrolyzerPower == ... gridPower + storagePower + ... data.solarProfile.*solarRating + ... data.windProfile.*windRating;
最適化問題を作成して解く
システムのコストを表にまとめます。
コスト | 金額 | 関連する変数 |
蓄電池のエネルギー | $354/kWh |
|
蓄電池の電力 | $1690/kW |
|
蓄電池の固定 | $5982 (1 回限りのコスト) | (なし) |
太陽光発電 | $1500/kW |
|
風力発電 | $1500/kW |
|
電解槽の電力 | $4000/kW |
|
グリッドの電力 |
|
|
NPV (正味現在価値) が次のように定義されることを思い出してください。
ここで、 は期間、 は期間の総数、 はキャッシュ フロー、 は割引率です。
各年のキャッシュ フローに適用する NPV 補正係数の配列を作成します。
NPV_correction = 1./((1+discount_rate).^(1:20));
年単位の間隔で NPV 補正を適用するには、グリッドからの電力の購入とグリッドへの電力の売却の両方による年間キャッシュ フローを計算します。
gridCashFlow = gridPower.*data.priceGrid; gridCashFlowAnnual = sum(reshape(gridCashFlow,numYears,8760),2);
同様に、水素の売却によるキャッシュ フローを計算します。水素の売却間隔は時間単位ではなく週単位であるため、各年のキャッシュ フローの計算はより複雑になります。
priceH2_sellTimes = data.priceH2(H2SellInterval:H2SellInterval:numSteps); H2cashFlow = H2_sold.*priceH2_sellTimes; H2cashFlowAnnual = optimexpr(numYears,1); j = 1; % year counter for i = 1:size(H2cashFlow,1) if i > j*numSteps/(numYears*H2SellInterval) j = j + 1; end H2cashFlowAnnual(j,1) = H2cashFlowAnnual(j,1) + H2cashFlow(i,1); end
NPV の式を定義し、NPV を問題の目的関数として設定します。ゴールは NPV の最大化であることを思い出してください。
NPV = dot(H2cashFlowAnnual,NPV_correction) - ... (dot(gridCashFlowAnnual,NPV_correction) + ... storageEnergyRating*storageEnergyCost + ... storagePowerRating*storagePowerCost + ... storageFixedCost + ... solarRating*solarPowerCost + ... windRating*windPowerCost + ... electrolyzerPowerRating*electrolyzerPowerCost); H2productionProblem.Objective = NPV;
最適化問題を解くには、solve 関数を呼び出します。solve は、問題定義から適切なソルバーを自動的に選択します。solve のオプションを設定するには、どのソルバーがこの問題の既定かを調べます。
defaultSolver = solvers(H2productionProblem)
defaultSolver = "linprog"
次に、linprog ソルバーが "interior-point" アルゴリズムを使用するようにオプションを設定します。このアルゴリズムは通常、大規模な問題の場合に効率的です。長時間かかる解法プロセス中にソルバーを監視するには、反復表示を指定します。
opt = optimoptions("linprog",Display="iter",Algorithm="interior-point");
解法プロセスの時間を測定しながら、solve を呼び出します。
tic [sol,fval,exitflag,output] = solve(H2productionProblem,Options=opt);
Solving problem using linprog.
LP preprocessing removed 1 inequalities, 350400 equalities,
350400 variables, and 174163 non-zero elements.
Iter Fval Primal Infeas Dual Infeas Complementarity
0 2.018450e+07 8.226336e+10 7.929518e+04 3.964759e+04
1 1.552183e+07 7.044826e+10 4.401464e+04 2.851580e+04
2 1.356020e+07 6.532633e+10 4.385490e+04 2.840865e+04
3 9.200252e+06 5.593844e+10 3.668795e+04 2.601673e+04
4 9.357494e+06 5.506621e+10 3.615345e+04 2.556162e+04
5 4.343854e+06 4.234017e+10 1.943619e+04 1.942665e+04
6 3.663265e+06 4.081119e+10 1.929830e+04 1.918952e+04
7 3.485725e+06 4.022795e+10 1.750641e+04 1.909905e+04
8 1.164683e+06 3.245046e+10 1.739851e+04 1.789185e+04
9 -6.963977e+05 2.433568e+10 1.299994e+04 1.662839e+04
10 -1.126482e+06 9.768712e+09 3.738028e+03 1.434624e+04
11 -9.687063e+05 8.032400e+09 2.792419e+03 1.547206e+04
12 -9.468808e+05 7.352327e+09 2.455865e+03 1.453425e+04
13 -8.833332e+05 3.687013e+09 1.998453e+03 1.338917e+04
14 -7.277230e+05 1.715294e+09 8.500309e+02 1.071701e+04
15 -7.436108e+05 1.498642e+09 8.230177e+02 1.037671e+04
16 -1.074011e+06 8.261753e+08 7.441277e+02 9.379018e+03
17 -1.077624e+06 8.245123e+08 7.245774e+02 9.132715e+03
18 -1.226810e+06 6.261597e+08 7.225536e+02 9.107218e+03
19 -1.266135e+06 5.950300e+08 6.306165e+02 8.377604e+03
20 -1.372968e+06 4.214008e+08 5.631281e+02 7.899575e+03
21 -1.549299e+06 1.824030e+08 4.472333e+02 6.574444e+03
22 -1.626012e+06 9.120146e+04 9.807344e+00 3.695863e+03
23 -1.622792e+06 4.560073e+01 9.560155e-03 1.362373e+01
24 -8.064141e+05 2.127121e+01 3.678170e-03 1.916751e+01
25 -4.678312e+05 1.557951e+01 2.700289e-03 1.756024e+01
26 -4.627417e+05 1.547614e+01 2.699102e-03 1.754751e+01
27 -3.805279e+05 1.390284e+01 1.161992e-03 5.257968e+00
28 -3.670200e+05 1.044264e+01 1.080932e-03 2.826650e+00
29 -1.955032e+05 7.452452e+00 6.067237e-04 5.262977e+00
Iter Fval Primal Infeas Dual Infeas Complementarity
30 -1.834978e+05 6.736750e+00 6.053788e-04 6.796647e+00
31 -1.650436e+05 6.438945e+00 5.036610e-04 6.689471e+00
32 -2.698129e+04 4.394982e+00 3.238541e-04 7.299377e+00
33 -2.646554e+04 4.377763e+00 2.704182e-04 9.136283e+00
34 4.775113e+04 3.009570e+00 1.588434e-04 1.755189e+01
35 8.715253e+04 2.313734e+00 1.036529e-04 1.582682e+01
36 1.095374e+05 1.933172e+00 6.971713e-05 1.391112e+01
37 1.428280e+05 1.384880e+00 5.228584e-05 1.536791e+01
38 1.653059e+05 1.006606e+00 3.007598e-05 1.738325e+01
39 1.745924e+05 8.066753e-01 2.349982e-05 1.677252e+01
40 1.887234e+05 5.707941e-01 1.799345e-05 1.675065e+01
41 1.894661e+05 5.595033e-01 1.639836e-05 1.671120e+01
42 1.994373e+05 4.016306e-01 1.299087e-05 1.663295e+01
43 2.071318e+05 2.876110e-01 1.016935e-05 1.648997e+01
44 2.113263e+05 2.266574e-01 8.323093e-06 1.595836e+01
45 2.148295e+05 1.770347e-01 6.935740e-06 1.515705e+01
46 2.180868e+05 1.319762e-01 5.723765e-06 1.545211e+01
47 2.194061e+05 1.100278e-01 4.895371e-06 1.549773e+01
48 2.204827e+05 8.998842e-02 3.854651e-06 1.538815e+01
49 2.214611e+05 7.659881e-02 2.637180e-06 1.539659e+01
50 2.231041e+05 5.602257e-02 1.498145e-06 1.124591e+01
51 2.240638e+05 4.512802e-02 7.528389e-07 9.045476e+00
52 2.256579e+05 2.853341e-02 4.992136e-07 5.702067e+00
53 2.267204e+05 1.776539e-02 3.628167e-07 4.005795e+00
54 2.269046e+05 1.598756e-02 3.339862e-07 4.006549e+00
55 2.274924e+05 1.039321e-02 1.411994e-07 4.011043e+00
56 2.276517e+05 9.014455e-03 9.943557e-08 4.010769e+00
57 2.279885e+05 6.211416e-03 6.882643e-08 4.010103e+00
58 2.282015e+05 4.492601e-03 4.924503e-08 3.010547e+00
59 2.283730e+05 3.131676e-03 4.810175e-07 2.097811e+00
Iter Fval Primal Infeas Dual Infeas Complementarity
60 2.284716e+05 2.384796e-03 4.118093e-06 1.623020e+00
61 2.285782e+05 1.581911e-03 2.482488e-06 1.645759e+00
62 2.286907e+05 8.093256e-04 1.824487e-06 1.526011e+00
63 2.287277e+05 5.715719e-04 3.074821e-06 1.080195e+00
64 2.287452e+05 4.695733e-04 2.948513e-06 8.883417e-01
65 2.287805e+05 2.663655e-04 5.353201e-06 5.044170e-01
66 2.288118e+05 1.039414e-04 2.921798e-05 1.971499e-01
67 2.288190e+05 7.158810e-05 1.314693e-05 1.357991e-01
68 2.288331e+05 1.787068e-05 2.169306e-06 3.369522e-02
69 2.288371e+05 4.840301e-06 7.612367e-06 8.511136e-03
70 2.288385e+05 1.677557e-06 9.943466e-07 2.397492e-03
71 2.288392e+05 5.499432e-07 7.753010e-09 7.948444e-06
72 2.288392e+05 5.638821e-07 6.120019e-10 1.028384e-07
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in feasible directions, to within the function tolerance, and constraints are satisfied to within the constraint tolerance.
toc
Elapsed time is 695.973725 seconds.
結果の解析
最適化された NPV を表示します。
optimizedNPV = fval
optimizedNPV = 2.2884e+05
NPV が正であるため、プロジェクトには経済的価値があります。
解析用に最適化の解の値を抽出します。
solarPowerVal = data.solarProfile*sol.solarRating; solarPowerRatingVal = sol.solarRating; windPowerVal = data.windProfile*sol.windRating; windPowerRatingVal = sol.windRating; gridPowerVal = sol.gridPower; storagePowerVal = sol.storagePower; storagePowerRatingVal = sol.storagePowerRating; storageEnergyRatingVal = sol.storageEnergyRating; electrolyzerPowerVal = sol.electrolyzerPower; electrolyzerPowerRatingVal = sol.electrolyzerPowerRating;
解の変数を表示する table を作成します。
systemComponents = ["Solar Power Rating (kW)";"Wind Power Rating (kW)"; ... "Storage Power Rating (kW)";"Storage Energy Rating (kWh)"; ... "Electrolyzer Power Rating (kW)"]; lowerBounds = zeros(5,1); upperBounds = [maxSolarRating; maxWindRating; maxStoragePowerRating;... maxStorageEnergyRating; maxElectrolyzerPowerRating]; optimizedRatings = [solarPowerRatingVal; windPowerRatingVal; storagePowerRatingVal; ... storageEnergyRatingVal; electrolyzerPowerRatingVal]; resultsTable = table(systemComponents,lowerBounds,upperBounds,optimizedRatings)
resultsTable=5×4 table
systemComponents lowerBounds upperBounds optimizedRatings
________________________________ ___________ ___________ ________________
"Solar Power Rating (kW)" 0 500 42.216
"Wind Power Rating (kW)" 0 500 114.54
"Storage Power Rating (kW)" 0 200 37.688
"Storage Energy Rating (kWh)" 0 10000 199.02
"Electrolyzer Power Rating (kW)" 0 50 50
電解槽の最適な電力定格は上限値の 50 です。この結果から、定格が 50 kW を超える電解槽を使用すると、プロジェクトの NPV が高くなる可能性があることがわかります。
システム動作の確認
システムの動作を詳しく確認します。まず、20 年間の時間ベクトルを作成します。
t1 = datetime(2024,1,1,0,0,0); t2 = datetime(2024 + numYears - 1,12,31,23,0,0); t = linspace(t1,t2,numSteps);
太陽光発電、風力発電、グリッドの電力、蓄電池の電力、負荷電力、および電解槽の電力の時系列データをプロットします。
figure p = plot(t,solarPowerVal,t,windPowerVal,t,gridPowerVal,"k",t,storagePowerVal,t, ... data.loadPower,"--",t,electrolyzerPowerVal,"--",LineWidth=2); grid legend("Solar Power","Wind Power","Grid Power","Storage Power","Load Power","Electrolyzer Power",Location="eastoutside") xlabel("Date and Time"),ylabel("Power (kW)")
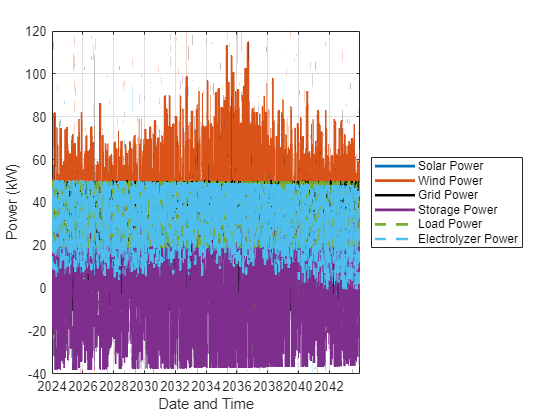
曲線をさらに詳しく確認するには、ズームインして 1 週間を表示します。
xlim([t(1e3),t(1e3+24*7)])
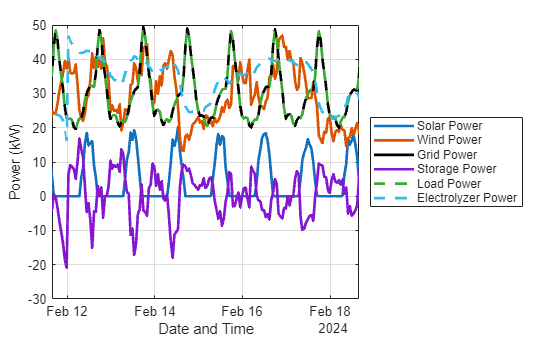
詳細レベルによって次のことがわかります。
グリッドの電力と負荷電力の曲線は同一です。この時間範囲では、負荷は完全にグリッドから供給されています。
蓄電池の電力は、太陽光発電が最大値に近づくと負になる傾向があります。蓄電池システムは、太陽光発電を利用できるときは太陽エネルギーを蓄積する傾向があり、太陽光発電を利用できないときは電力を供給します。
電解槽の電力は風力発電と相関関係にありますが、同一ではありません。
グリッドの電力とグリッドの価格プロファイルをプロットします。
figure plot(t,sol.gridPower,"k"); xlabel("Date and Time"),ylabel("Grid Power (kW)") grid hold on yyaxis right plot(t,data.priceGrid); ylabel("Grid Power Price ($/kW)") ylim([min(data.priceGrid) max(data.priceGrid)]) hold off
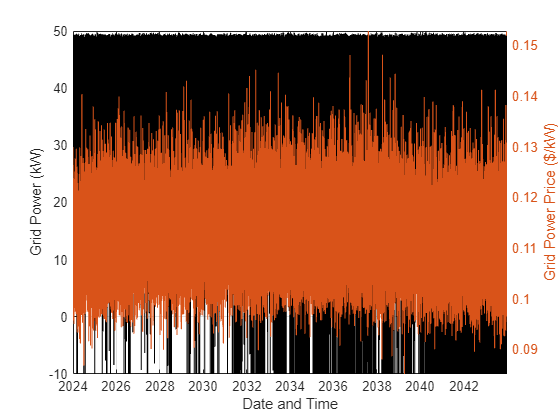
ズームインして詳しく調べます。
xlim([t(1e5) t(1.002e5)])
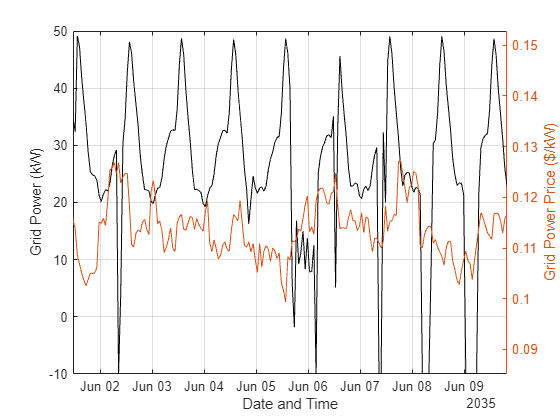
グリッドの電力が負になることがあり、グリッドに電力が売却されていることがわかります。
電力は通常、グリッドの価格が高いときにグリッドに売却されますが、必ずしもそうであるとは限りません。この結果により、このタイプの複雑な問題で判定を行うときに最適化を使用することの価値が浮き彫りになっています。
水素の累積売却量を計算してプロットします。
H2_sold_cum = cumsum(sol.H2_stored);
totalH2 = H2_sold_cum(end);
fprintf("Total H2 sold in kg: %g\n",totalH2)Total H2 sold in kg: 1.09694e+07
figure plot(t,H2_sold_cum); xlabel("Date and Time") ylabel("Cumulative Hydrogen Sold (kg)") grid
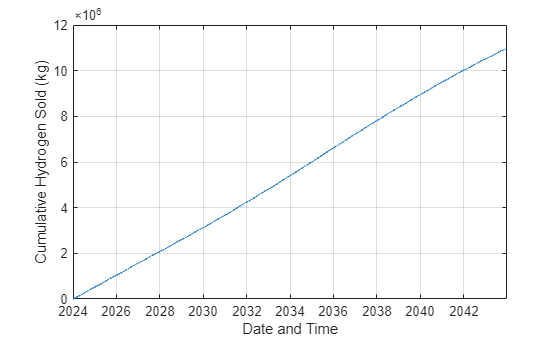
水素の累積売却量は (概ね) 時間とともに線形に増加しています。
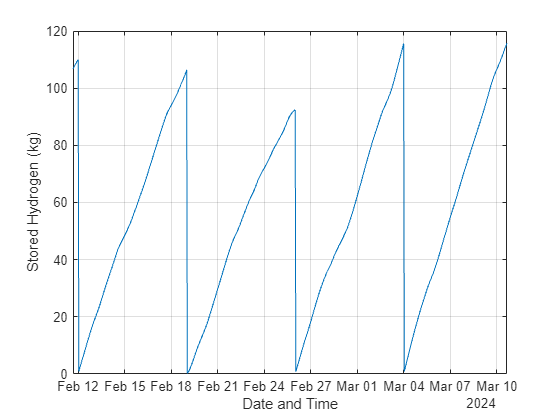
4 週間の蓄積された水素のプロファイルをプロットします。蓄積された水素は 1 週間増え続け、その週の最後に売却されると減少することに注目してください。
figure plot(t,sol.H2_stored); xlabel("Date and Time") ylabel("Stored Hydrogen (kg)") xlim([t(1e3),t(1e3+24*7*4)]) grid
割引率の変更
このシステムの経済性に割引率はどのように影響するでしょうか。さまざまな割引率の結果を計算します。この計算には長い時間がかかるため、利用可能な場合は並列計算を使用します。
nrates = 16; discountRate = linspace(.02,.08,nrates); % Create arrays to hold the results. sols = cell(nrates,1); fvals = zeros(1,nrates); opt.Display = "none"; allconstraints = H2productionProblem.Constraints; tic parfor i = 1:nrates NPVCorrection = 1./((1+discountRate(i)).^(1:numYears)); NPV = dot(H2cashFlowAnnual,NPVCorrection) - ... (dot(gridCashFlowAnnual,NPVCorrection) + ... storageEnergyRating*storageEnergyCost + ... storagePowerRating*storagePowerCost + ... storageFixedCost + ... solarRating*solarPowerCost + ... windRating*windPowerCost + ... electrolyzerPowerRating*electrolyzerPowerCost); H2productionProblem = optimproblem(Objective=NPV,... Constraints=allconstraints,ObjectiveSense="max"); [tempsol,tempfval] = solve(H2productionProblem,Options=opt); sols{i} = tempsol; fvals(i) = tempfval; end
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 4 workers.
toc
Elapsed time is 2822.702064 seconds.
NPV を割引率の関数としてプロットします。
figure plot(discountRate,fvals,"bo") xlabel("Discount Rate") ylabel("NPV")
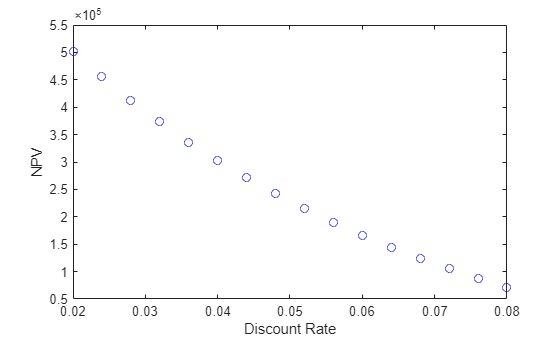
割引率が 2% から 8% に増加すると、最適な NPV は 5e5 から 7e4 に滑らかに減少します。最適曲線は凸のように見えます。これは、NPV が小さいときは割引率の変化の影響を受けやすくなり、NPV が大きいときは影響をあまり受けないことを示しています。
太陽光発電、風力発電、蓄電池、および電解槽の最適な定格がさまざまな割引率からどのような影響を受けるかをプロットします。
solarPowerRatings = zeros(1,nrates); windPowerRatings = zeros(1,nrates); storagePowerRatings = zeros(1,nrates); storageEnergyRatings = zeros(1,nrates); electrolyzerPowerRatings = zeros(1,nrates); Total_H2_Sold = zeros(1,nrates); for i = 1:nrates solarPowerRatings(i) = sols{i}.solarRating; windPowerRatings(i) = sols{i}.windRating; storagePowerRatings(i) = sols{i}.storagePowerRating; storageEnergyRatings(i) = sols{i}.storageEnergyRating; electrolyzerPowerRatings(i) = sols{i}.electrolyzerPowerRating; Total_H2_Sold(i) = sum(sols{i}.H2_stored); end figure tiledlayout(3,2,TileSpacing="tight") nexttile plot(discountRate,solarPowerRatings,"bo") xlabel("Discount Rate") ylabel("Solar Power") nexttile plot(discountRate,windPowerRatings,"bo") xlabel("Discount Rate") ylabel("Wind Power") nexttile plot(discountRate,storagePowerRatings,"bo") xlabel("Discount Rate") ylabel("Storage Power") nexttile plot(discountRate,storageEnergyRatings,"bo") xlabel("Discount Rate") ylabel("Storage Energy") nexttile plot(discountRate,electrolyzerPowerRatings,"bo") xlabel("Discount Rate") ylabel("Electrolyzer Power") ylim([49 50]) nexttile plot(discountRate,Total_H2_Sold,"bo") xlabel("Discount Rate") ylabel("Total H2 Sold")
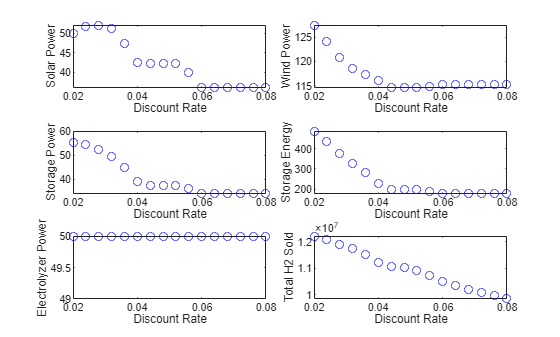
太陽光発電の定格は、割引率の単調関数ではありません。観測される最も高い太陽光発電の最適な定格は約 52 kW で、最も小さい定格は約 36 kW です。
同様に、風力発電の定格が割引率から受ける影響も単調ではありません。観測される最も高い風力発電の定格はほぼ 128 kW で、最も低い定格は 114 kW をわずかに上回ります。
蓄電池の電力定格は増加していません。観測される最も高い蓄電池の電力定格は 55 kW で、最も低い定格は 34 kW です。
同様に、蓄電池のエネルギー定格も増加していません。観測される最も高い蓄電池のエネルギー定格はほぼ 500 kWh で、最も低い定格は 200 kWh をわずかに下回ります。
電解槽の最適な電力定格はすべての割引率で 50 kW です。この結果から、電解槽の電力定格を高くすると NPV を向上できることがわかります。
20 年間の合計水素売却量は割引率増加で単調に減少し、凹でも凸でもありません。観測される最も多い水素売却量は 1.2e7 kg を上回り、最も少ない売却量は 1e7 kg をわずかに下回ります。
まとめ
グリーン水素製造システムの解析により、システムが 2% ~ 8% のすべての割引率の使用について経済的であることがわかります。システムの動作の詳細から、さまざまな割引率の影響を受けて予期しない変化がいくつか生じることがわかります。具体的には、システム コンポーネントの定格が厳密に割引率の単調関数ではありません。システム動作の確認のセクションで説明したように、最適解にはさまざまなシステム コンポーネントの 1 時間ごとの設定が含まれます。