このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

ソルバーベースの最適化ライブ エディター タスクの概要

このサンプル スクリプトは、ソルバーベースの "最適化" ライブ エディター タスクを使用した最適化や方程式解法を示しています。独自の問題に合わせてスクリプトを修正してください。

このスクリプトは、非線形制約を伴う非線形最適化問題を解きます。

パラメーターまたはデータの挿入

通常は、データや値をソルバーに渡します。これらの値を入力セクション (x0 が表示されている) に入力し、[セクション]、[セクションの実行] を選択するか、Control+Enter を押すことによってセクションを実行します。

初期点 x0 を設定し、最適化するために a をスケールします。

x0 = [2;1];
a = 100;

先に進む前にこのセクションを実行することによって、x0 の値と他の問題データをワークスペースに配置します。

最適化ライブ エディター タスク

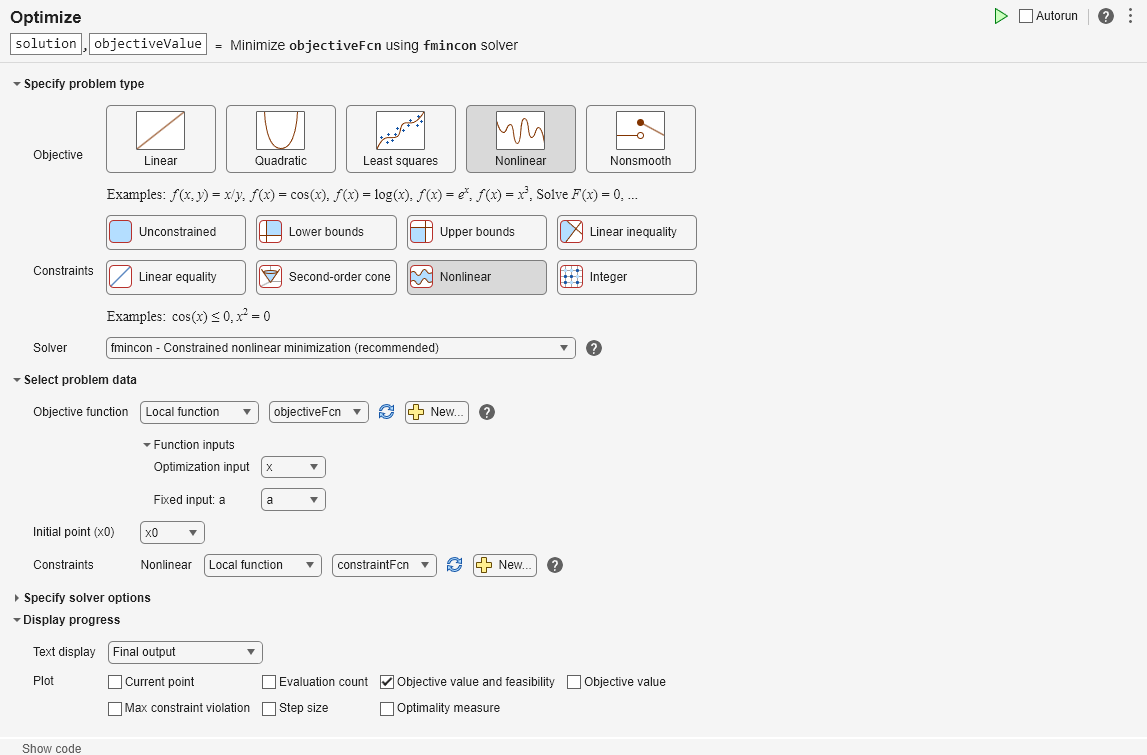
通常は、[ライブ エディター] タブで [タスク] > [最適化] を選択するか、または [挿入] タブで [タスク] > [最適化] を選択して、最適化ライブ エディター タスクをスクリプトに配置します。このとき、次の選択肢が表示されます。(これは単なるイメージで、実際のタスクではありません。)

ソルバーベースのタスクを選択するには、[ソルバーベース] をクリックします。

次のソルバーベースのタスクには、目的関数と非線形制約関数が含まれています。これらの関数を変更するには、タスクの下の関数リストを編集します。

制約を変更するには、該当する制約タイプを選択して、入力ボックスに値を入力します。上記の x0 が含まれるセクションに値を入力して、そのセクションを実行し、ワークスペースに値を配置しなければならない場合があります。

左側の縞模様のバーをクリックする、[実行] または [セクション]、[セクションの実行] を選択する、あるいは Control+Enter を押すことによって、タスクを実行します。

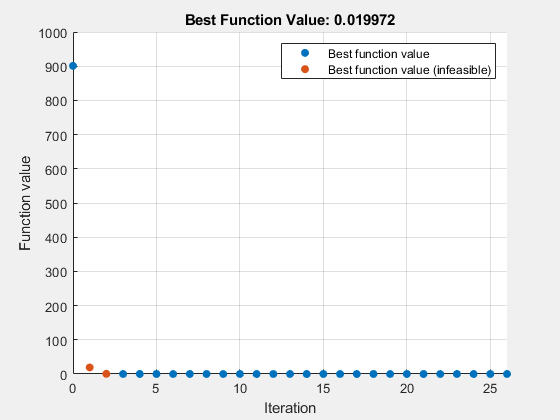
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

結果

Optimize は、解をワークスペース変数 solution に保存し、その解での目的関数値をワークスペース変数 objectiveValue に保存します。Optimize タスクの一番上でこれらの変数名を表示して変更できます。

これらの変数を表示します。

solution

solution = 2×1

    1.1413
    1.3029

objectiveValue

objectiveValue = 
0.0200

解での非線形制約関数値を表示します。

[ccons,ceqcons] = constraintFcn(solution)

ccons = 1×2

   -2.0000   -0.0000

ceqcons =

     []

補助関数 - ローカル関数

次のコードは目的関数を作成します。独自の問題に合わせてこのコードを修正してください。

function f = objectiveFcn(x,a)
f = a*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
end

次のコードは制約関数を作成します。独自の問題に合わせてこのコードを修正してください。

function [c,ceq] = constraintFcn(x)
c(1) = x(1)^2 + x(2)^2 - 5;
c(2) = 3 - x(1)^2 - x(2)^2;
ceq = [];  % No equality constraints
end

参考

最適化

トピック

• ソルバーベースの [最適化] ライブ エディター タスクの効果的な使い方
• ライブ スクリプトへの対話型タスクの追加
• How to Use the Optimize Live Editor Task