fminsearch アルゴリズム

fminsearch は、Lagarias らの [57] で説明されている Nelder-Mead のシンプレックス アルゴリズムを使用します。このアルゴリズムは n 次元のベクトル x に対して、n + 1 点のシンプレックスを使用します。このアルゴリズムはまず始めに、x₀(i) の要素の 5% を x₀ に加え、これらの n ベクトルをx₀ に付け加えてシンプレックスの要素として使用し、初期推定 x₀ のまわりにシンプレックスを作成します(x₀(i) = 0 の場合は、アルゴリズムが要素 i として 0.00025 を使用します)。次にアルゴリズムは以下の手順に従い、シンプレックスを繰り返し変更します。

メモ

fminsearch 反復表示のためのキーワードは、手順の説明後に [ ] 付きで表示されます。

1. x(i) が現在のシンプレックスの点のリスト i = 1,...,n + 1 を示すとします。

2. 最小の関数値 f(x(1)) から最大の関数値 f(x(n + 1)) へシンプレックスの点を並べます。反復の各ステップにおいて、アルゴリズムは現在の最悪の点 x(n + 1) を破棄し、他の点をシンプレックスにします (あるいは、次の手順 7 の場合に、f(x(1)) より大きい値をもつすべての n 点が変更されます)。

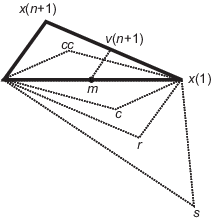
3. "反射" 点の生成

   r = 2m – x(n + 1),

   ここで、

   m = Σx(i)/n, i = 1...n

   そして、f(r) を計算します。

4. f(x(1)) ≤ f(r) < f(x(n)) の場合、r を採用し、この反復を終了します。[反射]

5. f(r) < f(x(1)) の場合、拡張点 s を計算し、

   s = m + 2(m – x(n + 1)),

   そして、f(s) を計算します。

   1. f(s) < f(r) の場合、s を採用してこの反復を終了します。[展開]

   2. そうでない場合は r を採用し、この反復を終了します。[反射]

6. f(r) ≥ f(x(n)) の場合は、m と x(n + 1) または r (目的関数値の小さい方) の間で "縮小" を実行します。

   1. f(r) < f(x(n + 1)) (つまり、r の方が x(n + 1) より正確) の場合は、次を計算します。

      c = m + (r – m)/2

      そして、f(c) を計算します。f(c) < f(r) の場合、c を採用してこの反復を終了します。外側に縮小

      そうでない場合は、手順 7 (収縮) に進みます。

   2. f(r) ≥ f(x(n + 1)) の場合、

      cc = m + (x(n + 1) – m)/2

      そして、f(cc) を計算します。f(cc) < f(x(n + 1)) の場合、cc を採用してこの反復を終了します。内側に縮小

      そうでない場合は、手順 7 (収縮) に進みます。

7. n 点を計算します

   v(i) = x(1) + (x(i) – x(1))/2

   そして、f(v(i)) (i = 2,...,n + 1) を計算します。次の反復でシンプレックスは x(1), v(2),...,v(n + 1) です。[収縮]

以下の図は、fminsearch が新しい各シンプレックスと共にステップで計算するであろう点を示します。元のシンプレックスは太い外側の線で示されます。反復は停止条件を満たすまで行われます。

参考

fminsearch

関連するトピック

• 制約なし非線形最適化アルゴリズム