解析的ヘッシアンを使用した fmincon の内点法アルゴリズム
この例では、導関数情報を使用して、解法プロセスをより迅速でロバストにする方法を説明します。fmincon の内点法アルゴリズムは入力にヘッセ関数を受け入れることができます。ヘッシアンを与えると、制約付き最小化問題は効率的に解くことができ、より正確な解を得ることができます。
補助関数 bigtoleft は、x(1) 座標が負の場合に急速に負になる目的関数です。その勾配は 3 要素のベクトルです。補助関数 bigtoleft のコードは、この例の終わりに掲載しています。
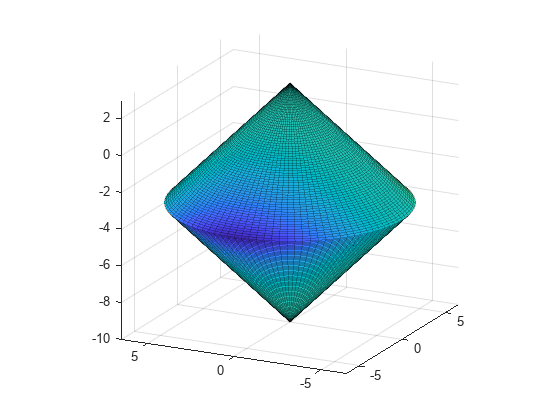
この例の制約集合は 2 つの円錐の内部交差部分です。1 つの円錐は上向きで、もう 1 つの円錐は下向きです。制約関数は各円錐に対して 1 つの要素を含む 2 要素のベクトルです。この例は 3 次元であるため、制約の勾配は 3 行 2 列の行列です。補助関数 twocone のコードは、この例の終わりに掲載しています。
この制約の Figure を作成します。色付けには目的関数を使用します。
% Create figure figure1 = figure; % Create axes axes1 = axes('Parent',figure1); view([-63.5 18]); grid('on'); hold('on'); % Set up polar coordinates and two cones r=0:.1:6.5; th=2*pi*(0:.01:1); x=r'*cos(th); y=r'*sin(th); z=-10+sqrt(x.^2+y.^2); zz=3-sqrt(x.^2+y.^2); % Evaluate objective function on cone surfaces newxf=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000; newxg=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000; % Create lower surf with color set by objective surf(x,y,z,newxf,'Parent',axes1,'EdgeAlpha',0.25); % Create upper surf with color set by objective surf(x,y,zz,newxg,'Parent',axes1,'EdgeAlpha',0.25); axis equal
ヘッセ関数の作成
fmincon ソルバーで 2 次導関数情報を使用するには、ラグランジュ関数のヘッシアンを作成しなければなりません。ラグランジュ関数のヘッシアンは次の式で与えられます。
ここで、 は関数 bigtoleft であり、 は 2 つの円錐制約関数です。補助関数 hessinterior (この例の終わりに掲載) が、点 x におけるラグランジュ関数のヘッシアンをラグランジュ乗数構造体 lambda を使用して計算します。この関数は、まず を計算します。次いで、2 つの制約ヘッシアン および を計算してから、これらを対応するラグランジュ乗数 lambda.ineqnonlin(1) および lambda.ineqnonlin(2) で乗算し、その積を加算します。 となることを制約関数 twocone の定義から確認できます。これによって計算を簡略化します。
導関数を使用するためのオプションの作成
fmincon で目的勾配、制約勾配、およびヘッシアンを使用できるようにするには、適切なオプションを設定しなければなりません。ラグランジュ関数のヘッシアンを使用する HessianFcn オプションは、内点法アルゴリズムに対してのみ利用可能です。
options = optimoptions('fmincon','Algorithm','interior-point',... "SpecifyConstraintGradient",true,"SpecifyObjectiveGradient",true,... 'HessianFcn',@hessinterior);
すべての導関数情報を使用する最小化
初期点 x0 = [-1,-1,-1] を設定します。
x0 = [-1,-1,-1];
この問題には、線形制約または範囲がありません。これらの引数を [] に設定します。
A = []; b = []; Aeq = []; beq = []; lb = []; ub = [];
問題を解きます。
[x,fval,eflag,output] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
解および解法プロセスの検証
解、目的関数値、終了フラグおよび関数評価と反復の回数を調べます。
disp(x)
-6.5000 -0.0000 -3.5000
disp(fval)
-2.8941e+03
disp(eflag)
1
disp([output.funcCount,output.iterations])
7 6
ヘッセ関数を使用しない場合、fmincon は収束に向けた反復回数が多くなり、関数評価回数もより多く必要となります。
options.HessianFcn = [];
[x2,fval2,eflag2,output2] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
disp([output2.funcCount,output2.iterations])
13 9
また、勾配情報を含めない場合、fmincon が実行する反復回数は変わりませんが、さらに多くの関数評価が必要になります。
options.SpecifyConstraintGradient = false;
options.SpecifyObjectiveGradient = false;
[x3,fval3,eflag3,output3] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
disp([output3.funcCount,output3.iterations])
43 9
補助関数
次のコードは、bigtoleft 補助関数を作成します。
function [f gradf] = bigtoleft(x) % This is a simple function that grows rapidly negative % as x(1) becomes negative % f = 10*x(:,1).^3+x(:,1).*x(:,2).^2+x(:,3).*(x(:,1).^2+x(:,2).^2); if nargout > 1 gradf=[30*x(1)^2+x(2)^2+2*x(3)*x(1); 2*x(1)*x(2)+2*x(3)*x(2); (x(1)^2+x(2)^2)]; end end
次のコードは、twocone 補助関数を作成します。
function [c ceq gradc gradceq] = twocone(x) % This constraint is two cones, z > -10 + r % and z < 3 - r ceq = []; r = sqrt(x(1)^2 + x(2)^2); c = [-10+r-x(3); x(3)-3+r]; if nargout > 2 gradceq = []; gradc = [x(1)/r,x(1)/r; x(2)/r,x(2)/r; -1,1]; end end
次のコードは、hessinterior 補助関数を作成します。
function h = hessinterior(x,lambda) h = [60*x(1)+2*x(3),2*x(2),2*x(1); 2*x(2),2*(x(1)+x(3)),2*x(2); 2*x(1),2*x(2),0];% Hessian of f r = sqrt(x(1)^2+x(2)^2);% radius rinv3 = 1/r^3; hessc = [(x(2))^2*rinv3,-x(1)*x(2)*rinv3,0; -x(1)*x(2)*rinv3,x(1)^2*rinv3,0; 0,0,0];% Hessian of both c(1) and c(2) h = h + lambda.ineqnonlin(1)*hessc + lambda.ineqnonlin(2)*hessc; end