このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

常微分方程式 (ODE) の適合

この例では、ODE のパラメーターをデータに当てはめる 2 通りの方法を示します。1 番目は、ローレンツ方程式 (初期パラメーター鋭敏性を備えた有名な ODE) の解の一部に一定速度の循環パスを直接当てはめる方法を示します。2 番目は、ローレンツ方程式のパラメーターを変更して一定速度の循環パスを当てはめる方法を示します。微分方程式をデータに当てはめるためのモデルとして、自分の用途に適したアプローチを使用できます。

ローレンツ方程式: 定義と数値的な解

ローレンツ方程式は連立常微分方程式です (ローレンツ方程式を参照)。実定数 $$\sigma ,\rho ,\beta$$ について、方程式は以下になります。

$$\begin{array}{l}\frac{dx}{dt}=\sigma (y-x)\\ \frac{dy}{dt}=x(\rho -z)-y\\ \frac{dz}{dt}=xy-\beta z.\end{array}$$

鋭敏性の高い方程式の場合、ローレンツのパラメーターの値は、$$\sigma =10,\beta =8/3,\rho =28$$ です。方程式を [x(0),y(0),z(0)] = [10,20,10] から始め、時間 0 から 100 までの方程式の変化を表示します。

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
xt0 = [10,20,10];
[tspan,a] = ode45(f,[0 100],xt0);     % Runge-Kutta 4th/5th order ODE solver
figure
plot3(a(:,1),a(:,2),a(:,3))
view([-10.0 -2.0])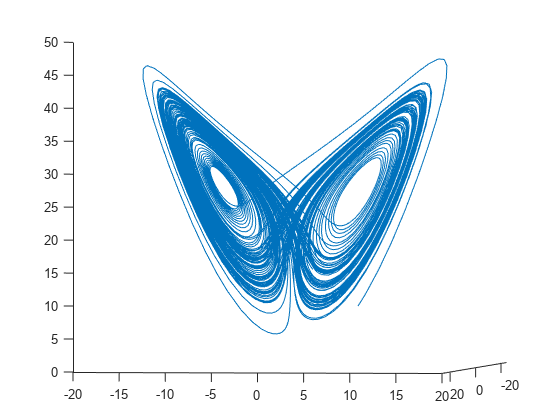

変化はかなり複雑です。ただし、短い時間間隔では、均一な循環動作に見えます。時間間隔 [0,1/10] にわたり、解をプロットします。

[tspan,a] = ode45(f,[0 1/10],xt0);     % Runge-Kutta 4th/5th order ODE solver
figure
plot3(a(:,1),a(:,2),a(:,3))
view([-30 -70])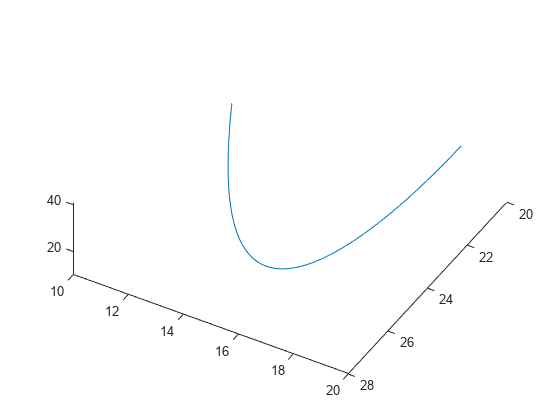

循環パスの ODE 解への適合

循環パスの方程式にはいくつかのパラメーターがあります。

• x-y 平面からのパスの角度 $$\theta (1)$$

• x 軸に沿った傾斜からの平面の角度 $$\theta (2)$$

• 半径 R

• 速度 V

• 時間 0 からのシフト t0

• 空間 delta における 3 次元シフト

これらのパラメーターに関して、時間 xdata の循環パスの位置を決定します。

type fitlorenzfn

function f = fitlorenzfn(x,xdata)

theta = x(1:2);
R = x(3);
V = x(4);
t0 = x(5);
delta = x(6:8);
f = zeros(length(xdata),3);
f(:,3) = R*sin(theta(1))*sin(V*(xdata - t0)) + delta(3);
f(:,1) = R*cos(V*(xdata - t0))*cos(theta(2)) ...
    - R*sin(V*(xdata - t0))*cos(theta(1))*sin(theta(2)) + delta(1);
f(:,2) = R*sin(V*(xdata - t0))*cos(theta(1))*cos(theta(2)) ...
    - R*cos(V*(xdata - t0))*sin(theta(2)) + delta(2);

ODE 解での所定の時間における、ローレンツ方程式への最適適合循環パスを求めるには、lsqcurvefit を使用します。パラメーターを妥当な範囲内に留めるよう、さまざまなパラメーターに範囲を設けます。

lb = [-pi/2,-pi,5,-15,-pi,-40,-40,-40];
ub = [pi/2,pi,60,15,pi,40,40,40];
theta0 = [0;0];
R0 = 20;
V0 = 1;
t0 = 0;
delta0 = zeros(3,1);
x0 = [theta0;R0;V0;t0;delta0];
[xbest,resnorm,residual] = lsqcurvefit(@fitlorenzfn,x0,tspan,a,lb,ub);

Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

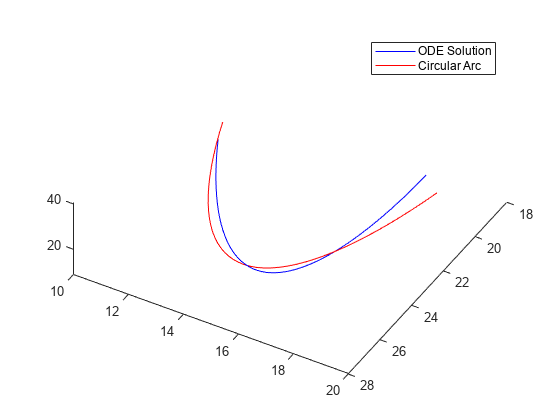
ODE 解からの時間における最適適合循環パスを、ローレンツ方程式の解と一緒にプロットします。

soln = a + residual;
hold on
plot3(soln(:,1),soln(:,2),soln(:,3),'r')
legend('ODE Solution','Circular Arc')
hold off

figure
plot3(a(:,1),a(:,2),a(:,3),'b.','MarkerSize',10)
hold on
plot3(soln(:,1),soln(:,2),soln(:,3),'rx','MarkerSize',10)
legend('ODE Solution','Circular Arc')
hold off

ODE の円弧への適合

ここで、パラメーター $$\sigma ,\beta ,and\rho$$ を円弧への最適適合となるように変更します。さらに適した適合となるように、初期点 [10,20,10] を変更できます。

これを行うには、関数ファイル paramfun を記述します。このファイルは、ODE 適合のパラメーターをとり、時間 t にわたる軌跡を計算します。

type paramfun

function pos = paramfun(x,tspan)

sigma = x(1);
beta = x(2);
rho = x(3);
xt0 = x(4:6);
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
[~,pos] = ode45(f,tspan,xt0);

最適なパラメーターを見つけるには、lsqcurvefit を使用して、新たに計算された ODE 軌跡と円弧 soln との間の差を最小化します。

xt0 = zeros(1,6);
xt0(1) = sigma;
xt0(2) = beta;
xt0(3) = rho;
xt0(4:6) = soln(1,:);
[pbest,presnorm,presidual,exitflag,output] = lsqcurvefit(@paramfun,xt0,tspan,soln);

Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

この最適化でパラメーターがどの程度変化したかを判別します。

fprintf('New parameters: %f, %f, %f',pbest(1:3))

New parameters: 9.132446, 2.854998, 27.937986

fprintf('Original parameters: %f, %f, %f',[sigma,beta,rho])

Original parameters: 10.000000, 2.666667, 28.000000

パラメーター sigma と beta は、約 10% ずつ変化しました。

変更済みの解をプロットします。

figure
hold on
odesl = presidual + soln;
plot3(odesl(:,1),odesl(:,2),odesl(:,3),'b')
plot3(soln(:,1),soln(:,2),soln(:,3),'r')
legend('ODE Solution','Circular Arc')
view([-30 -70])
hold off

ODE の適合における問題

シミュレーションまたは常微分方程式の最適化で説明されているとおり、オプティマイザーでは、数値的 ODE 解に固有のノイズに起因する問題が生じることがあります。正確でない可能性があることを終了メッセージまたは終了フラグが示しているなどの理由で、解が理想的でないと疑われる場合は、有限差分の変更を試みてください。この例では、より大きな有限差分ステップ サイズと中心有限差分を使用します。

options = optimoptions('lsqcurvefit','FiniteDifferenceStepSize',1e-4,...
    'FiniteDifferenceType','central');
[pbest2,presnorm2,presidual2,exitflag2,output2] = ...
    lsqcurvefit(@paramfun,xt0,tspan,soln,[],[],options);

Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

この場合、これらの有限差分オプションを使用しても、解は改善されません。

disp([presnorm,presnorm2])

   20.0637   20.0637

参考

トピック

• 離散化された最適軌跡 (問題ベース)
• シミュレーションまたは常微分方程式の最適化