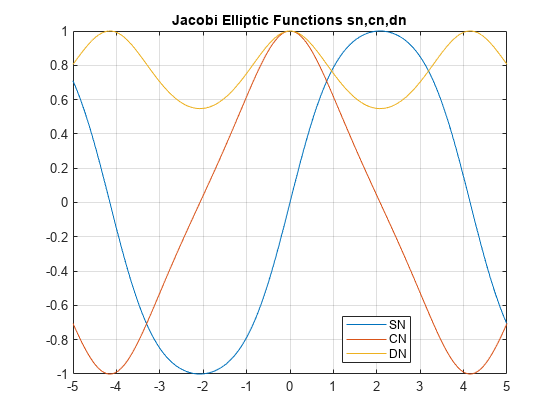
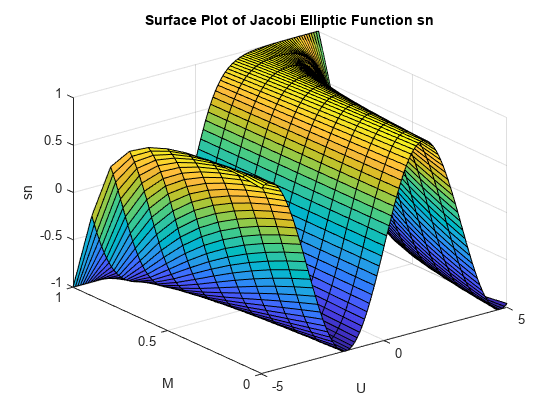
ellipj

ヤコビ楕円関数

構文

[SN,CN,DN] = ellipj(U,M)

[SN,CN,DN] = ellipj(U,M,tol)

説明

[SN,CN,DN] = ellipj(U,M) は、引数 U とパラメーター M の対応要素に関して評価された、ヤコビ楕円関数 SN、CN、DN を返します。入力 U と M は同じサイズであるか、U または M のいずれかがスカラーでなければなりません。

[SN,CN,DN] = ellipj(U,M,tol) は、精度 tol でヤコビ楕円関数を計算します。tol の既定値は eps です。tol を大きくすると計算精度は低くなりますが、より高速に計算が行われます。

例

ヤコビ楕円関数の検出

U = 0.5 および M = 0.25 であるヤコビ楕円関数を求めます。

[s,c,d] = ellipj(0.5,0.25)

s = 
0.4751

c = 
0.8799

d = 
0.9714

ヤコビ楕円関数のプロット

-5≤U≤5 および M = 0.7 であるヤコビ楕円関数をプロットします。

M = 0.7;
U = -5:0.01:5;
[S,C,D] = ellipj(U,M);
plot(U,S,U,C,U,D);
legend('SN','CN','DN','Location','best')
grid on
title('Jacobi Elliptic Functions sn,cn,dn')

ヤコビ楕円関数 sn の表面プロットの生成

M の許容範囲および -5≤U≤5 でヤコビ楕円関数 sn の表面プロットを生成します。

[M,U] = meshgrid(0:0.1:1,-5:0.1:5);
S = ellipj(U,M);
surf(U,M,S)
xlabel('U')
ylabel('M')
zlabel('sn')
title('Surface Plot of Jacobi Elliptic Function sn')

許容誤差の変更によるヤコビ楕円積分の高速計算

tol の既定値は eps です。任意の M に対して既定値を用いた実行時間を tic と toc を使用して取得します。tol を 1000 倍に増やして実行時間を取得します。実行時間を比較します。

tic
ellipj(0.253,0.937)

ans = 
0.2479

toc

Elapsed time is 0.045461 seconds.

tic
ellipj(0.253,0.937,eps*1000)

ans = 
0.2479

toc

Elapsed time is 0.005111 seconds.

許容誤差を大幅に増やすと、ellipj は非常に速く実行されます。

入力引数

U — 入力配列

スカラー | ベクトル | 行列 | 多次元配列

入力配列。スカラー、ベクトル、行列または多次元配列として指定します。U は実数値に制限されます。U が非スカラーの場合、M はスカラーであるか、U と同じサイズの非スカラーでなければなりません。

データ型: single | double

M — 入力配列

スカラー | ベクトル | 行列 | 多次元配列

入力配列。スカラー、ベクトル、行列または多次元配列として指定します。M は 0≤ m ≤1 の値をとることができます。M が非スカラーの場合、U はスカラーであるか、M と同じサイズの非スカラーでなければなりません。M のその他の値は、[1] に記載されている変換式 16.10 と 16.11 を使用して、この範囲にマッピングします。

データ型: single | double

tol — 結果の精度

eps (既定値) | 非負の実数

結果の精度。非負の実数として指定します。既定値は eps です。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

出力引数

SN — ヤコビ楕円関数の sn

スカラー | ベクトル | 行列 | 多次元配列

ヤコビ楕円関数の sn。スカラー、ベクトル、行列または多次元配列として返されます。

CN — ヤコビ楕円関数の cn

スカラー | ベクトル | 行列 | 多次元配列

ヤコビ楕円関数の cn。スカラー、ベクトル、行列または多次元配列として返されます。

DN — ヤコビ楕円関数の dn

スカラー | ベクトル | 行列 | 多次元配列

ヤコビ楕円関数の dn。スカラー、ベクトル、行列または多次元配列として返されます。

詳細

ヤコビ楕円関数

ヤコビ楕円関数は、積分項で定義されます。

$$u={\displaystyle {\int }_0^{\varphi }\frac{d\theta }{\sqrt{1-m{\sin }^2\theta }}}.$$

以下のようになります。

$$sn(u)=\sin \varphi ,cn(u)=\cos \varphi ,dn(u)=\sqrt{1-m{\sin }^2\varphi }.$$

いくつかの楕円関数の定義では、パラメーター m の代わりに楕円係数 k またはモジュラー角 α を使用します。次式のような関係があります。

$$k^2=m={\sin }^{2}a.$$

ヤコビ楕円関数は、多くの数学的な恒等式に従います。良い例については、[1]を参照してください。

アルゴリズム

ellipj は、[1]の算術幾何平均を使って、ヤコビ楕円関数を計算します。3 つの値から始めます。

$$a_0=1,b_0=\sqrt{1-m},c_0=\sqrt{m}.$$

ellipj は以下の式を使用して次の反復を計算します。

$$\begin{array}{l}{a}_i=\frac{1}{2}(a_{i-1}+b_{i-1})\\ b_i={(}^{a_{i-1}}\\ c_i=\frac{1}{2}(a_{i-1}-b_{i-1}).\end{array}$$

次に、以下の式でラジアン単位で振幅を計算します。

$$\sin (2{\varphi }_{n-1}-{\varphi }_n)=\frac{c_n}{a_n}\sin ({\varphi }_n),$$

このとき、位相の連続性に注意してください。ヤコビ楕円関数は、簡単に以下の式で表されます。

$$\begin{array}{l}sn(u)=\sin {\varphi }_0\\ cn(u)=\cos {\varphi }_0\\ dn(u)=\sqrt{1-m\cdot sn{(u)}^2}.\end{array}$$

参照

[1] Abramowitz, M. and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

バージョン履歴

R2006a より前に導入

参考

ellipke