状態依存の強い質量行列による ODE の求解

この例では、移動メッシュ法 [1] を使用して Burger の方程式を解く方法を説明します。問題には質量行列が含まれます。また、強い状態依存と質量行列のスパース性を考慮したオプションが指定され、解法プロセスが効率化されています。

問題の設定

Burger の方程式は、次の PDE で与えられる移流拡散方程式です。

$$\frac{\partial \mathit{u}}{\partial \mathit{t}}=ϵ\frac{{\partial }^2\mathit{u}}{{\partial \mathit{x}}^2}-\frac{\partial }{\partial \mathit{x}}\left(\frac{{\mathit{u}}^2}{2}\right),0<\mathit{x}<1,\mathit{t}>0,ϵ=1{\times \mathrm{10}}^{-4}.$$

座標変換 ([1] の方程式 18) を適用すると、左辺の項数が追加されます。

$$\frac{\partial \mathit{u}}{\partial \mathit{t}}-\frac{\partial \mathit{u}}{\partial \mathit{x}}\frac{\partial \mathit{x}}{\partial \mathit{t}}=ϵ\frac{{\partial }^2\mathit{u}}{{\partial \mathit{x}}^2}-\frac{\partial }{\partial \mathit{x}}\left(\frac{{\mathit{u}}^2}{2}\right).$$

PDE から 1 変数の ODE への変換は、有限差分を使用して $\mathit{x}$ に対する偏導関数を近似することで実行されます。有限差分が $\Delta$ として記述されている場合、PDE は $\mathit{t}$ に対する導関数のみを含む ODE として書き換えることができます。

$$\frac{\mathit{du}}{\mathit{dt}}-\Delta \mathit{u}\frac{\mathit{dx}}{\mathit{dt}}=ϵ{\Delta }^2\mathit{u}-\Delta \left(\frac{{\mathit{u}}^2}{2}\right).$$

この形式では、ode15s など ODE ソルバーを使用して、$\mathit{u}$ および $\mathit{x}$ の解を経時的に求めることができます。

この例では、問題は $\mathit{N}$ 点からなる "移動" メッシュとして定式化されます。[1] に記述されている移動メッシュ法では、変化する領域に集中するよう、各タイム ステップにメッシュ点が配置されます。境界条件と初期条件は次のとおりです。

$$\begin{array}{l}\mathit{u}\left(0,\mathit{t}\right)=\mathit{u}\left(1,\mathit{t}\right)=0,\\ \mathit{u}\left(\mathit{x},0\right)=\sin \left(2\pi \mathit{x}\right)+\frac{1}{2}\sin \left(\pi \mathit{x}\right).\end{array}$$

与えられた $\mathit{N}$ 点の初期メッシュでは、求解すべき方程式が $2\mathit{N}$ 個あります。$\mathit{N}$ 個の方程式は Burger の方程式に対応し、$\mathit{N}$ 個の方程式は各メッシュ点の運動を特定します。したがって、最終的な連立方程式は次のようになります。

$$\begin{array}{l}\frac{\mathit{d}{\mathit{u}}_1}{\mathit{dt}}-\Delta {\mathit{u}}_1\frac{\mathit{d}{\mathit{x}}_1}{\mathit{dt}}=ϵ{\Delta }^2{\mathit{u}}_1-\Delta \left(\frac{{{\mathit{u}}_1}^2}{2}\right),\\ ⋮\\ \frac{\mathit{d}{\mathit{u}}_{\mathit{N}}}{\mathit{dt}}-\Delta {\mathit{u}}_{\mathit{N}}\frac{\mathit{d}{\mathit{x}}_{\mathit{N}}}{\mathit{dt}}=ϵ{\Delta }^2{\mathit{u}}_{\mathit{N}}-\Delta \left(\frac{{{\mathit{u}}_{\mathit{N}}}^2}{2}\right),\\ \frac{{\mathit{d}}^2\dot{{\mathit{x}}_1}}{\mathit{d}{\mathit{t}}^2}=\frac{1}{\tau }\frac{\mathit{d}}{\mathit{dt}}\left(\mathit{B}\left({\mathit{x}}_1,\mathit{t}\right)\frac{\mathit{d}{\mathit{x}}_1}{\mathit{dt}}\right),\\ ⋮\\ \frac{{\mathit{d}}^2\dot{{\mathit{x}}_{\mathit{N}}}}{\mathit{d}{\mathit{t}}^2}=\frac{1}{\tau }\frac{\mathit{d}}{\mathit{dt}}\left(\mathit{B}\left({\mathit{x}}_{\mathit{N}},\mathit{t}\right)\frac{\mathit{d}{\mathit{x}}_{\mathit{N}}}{\mathit{dt}}\right).\end{array}$$

移動メッシュの項は [1] の MMPDE6 に対応します。パラメーター $\tau$ はメッシュに等配分を強いる時間スケールを表します。項 $\mathit{B}\left(\mathit{x},\mathit{t}\right)$ は [1] の方程式 21 で示される監視関数です。

$$\mathit{B}\left(\mathit{x},\mathit{t}\right)=\sqrt{1+{\left(\frac{\mathit{d}{\mathit{u}}_{\mathit{i}}}{\mathit{d}{\mathit{x}}_{\mathit{i}}}\right)}^2}.$$

移動メッシュ点を使って Burger の方程式を解くためにこの例で使用されたアプローチでは、いくつかの手法が示されています。

• 連立方程式は質量行列による定式化 $\mathit{M}{\mathit{y}}^{\prime }=\mathit{f}\left(\mathit{t},\mathit{y}\right)$ を使用して表現されます。ode15s ソルバーに質量行列が関数として指定されます。

• 導関数には Burger の方程式に対応する方程式だけでなく、選択した移動メッシュを扱う一連の方程式も含まれます。

• ヤコビアン $\mathrm{dF}/\mathrm{dy}$ のスパース パターンとベクトルで乗算された質量行列の導関数 $\mathit{d}\left(\mathrm{Mv}\right)/\mathrm{dy}$ のスパース パターンが、ソルバーに関数として指定されます。これらのスパース パターンを指定することで、ソルバーの動作がより効率的になります。

• いくつかの偏導関数の近似には有限差分が使用されます。

MATLAB® でこの方程式を解くには、導関数、質量行列関数、ヤコビアン $\mathrm{dF}/\mathrm{dy}$ のスパース パターン関数、および $\mathit{d}\left(\mathrm{Mv}\right)/\mathrm{dy}$ のスパース パターン関数を記述します。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

質量行列のコード化

連立方程式の左辺には 1 階微分の線形結合があるため、質量行列ではすべての項が表現されている必要があります。連立方程式の左辺を $\mathit{M}{\mathit{y}}^{\prime }$ と等号で結び、この形式の質量行列を抽出します。質量行列はそれぞれが次数 $\mathit{N}$ の正方行列である、4 つのブロックで構成されます。

$\left[\begin{array}{c}\frac{\partial {\mathit{u}}_1}{\partial \mathit{t}}-\frac{\partial {\mathit{u}}_1}{\partial {\mathit{x}}_1}\frac{\partial {\mathit{x}}_1}{\partial \mathit{t}}\\ ⋮\\ \frac{\partial {\mathit{u}}_{\mathit{N}}}{\partial \mathit{t}}-\frac{\partial {\mathit{u}}_{\mathit{N}}}{\partial {\mathit{x}}_{\mathit{N}}}\frac{\partial {\mathit{x}}_{\mathit{N}}}{\partial \mathit{t}}\\ \frac{{\partial }^2\dot{{\mathit{x}}_1}}{\partial {\mathit{t}}^2}\\ ⋮\\ \frac{{\partial }^2\dot{{\mathit{x}}_{\mathit{N}}}}{\partial {\mathit{t}}^2}\end{array}\right]=\mathit{M}{\mathit{y}}^{\prime }=\left[\begin{array}{cc}{\mathit{M}}_1& {\mathit{M}}_2\\ {\mathit{M}}_3& {\mathit{M}}_4\end{array}\right]\left[\begin{array}{c}\dot{{\mathit{u}}_1}\\ ⋮\\ \dot{{\mathit{u}}_{\mathit{N}}}\\ \dot{{\mathit{x}}_1}\\ ⋮\\ \dot{{\mathit{x}}_{\mathit{N}}}\end{array}\right]$.

この定式化では、${\mathit{M}}_1$ と ${\mathit{M}}_2$ が Burger の方程式の左辺を形成し (連立方程式の最初の $\mathit{N}$ 個の方程式)、${\mathit{M}}_3$ と ${\mathit{M}}_4$ がメッシュの方程式の左辺を形成します (連立方程式の最後の $\mathit{N}$ 個の方程式)。ブロック行列は次のとおりです。

$$\begin{array}{l}{\mathit{M}}_1={\mathit{I}}_{\mathit{N}},\\ {\mathit{M}}_2=-\frac{\partial {\mathit{u}}_{\mathit{i}}}{\partial {\mathit{x}}_{\mathit{i}}}{\mathit{I}}_{\mathit{N}},\\ {\mathit{M}}_3=0_{\mathit{N}},\\ {\mathit{M}}_4=\frac{{\partial }^2}{\partial {\mathit{t}}^2}{\mathit{I}}_{\mathit{N}}.\end{array}$$

${\mathit{I}}_{\mathit{N}}$ は $\mathit{N}\times \mathit{N}$ の単位行列です。${\mathit{M}}_2$ の偏導関数は有限差分を使用して推定される一方、${\mathit{M}}_4$ の偏導関数ではラプラシアン行列が使用されます。${\mathit{M}}_3$ にはゼロのみが含まれることに注意してください。メッシュ運動の方程式はいずれも $\dot{\mathit{u}}$ に依存しないためです。

これで、質量行列を計算する関数を記述できます。関数は時間 $\mathit{t}$ と解ベクトル $\mathit{y}$ という 2 つの入力を受け入れなければなりません。解ベクトル $\mathit{y}$ は半分が $\dot{\mathit{u}}$ 要素でもう半分が $\dot{\mathit{x}}$ 要素であるため、関数ではまずこれらを抽出します。次に、関数は (問題の境界値を考慮して) すべてのブロック行列を形成し、4 つのブロックを使用して質量行列を組み立てます。

function M = mass(t,y)
% Extract the components of y for the solution u and mesh x
N = length(y)/2; 
u = y(1:N);
x = y(N+1:end);

% Boundary values of solution u and mesh x
u0 = 0;
uNP1 = 0;
x0 = 0;
xNP1 = 1;

% M1 and M2 are the portions of the mass matrix for Burgers' equation. 
% The derivative du/dx is approximated with finite differences, using 
% single-sided differences on the edges and centered differences in between.
M1 = speye(N);
i = 2:N-1;
v = [0; -(u(i+1) - u(i-1))./(x(i+1) - x(i-1)) ; 0];
M2 = spdiags(v,0,N,N);

M2(1,1) = - (u(2) - u0)/(x(2) - x0);
M2(N,N) = - (uNP1 - u(N-1))/(xNP1 - x(N-1));

% M3 and M4 define the equations for mesh point evolution, corresponding to 
% MMPDE6 in the reference paper. Since the mesh functions only involve d/dt(dx/dt), 
% the M3 portion of the mass matrix is all zeros. The second derivative in M4 is 
% approximated using a finite difference Laplacian matrix. 
M3 = sparse(N,N);
M4 = spdiags([1 -2 1],-1:1,N,N);

% Assemble mass matrix
M = [M1 M2; M3 M4];
end

メモ: 関数はすべて例の最後にローカル関数として含まれます。

導関数のコード化

この問題の導関数は $2\mathit{N}$ 個の要素をもつベクトルを返します。最初の $\mathit{N}$ 個の要素は Burger の方程式に対応し、残りの $\mathit{N}$ 個の要素は移動メッシュの方程式に対応します。関数 movingMeshODE は以下の手順を通して、連立方程式のすべての方程式の右辺を評価します。

1. 有限差分を使用して Burger の方程式を評価します (最初の $\mathit{N}$ 個の要素)。

2. 監視関数を評価します (最後の $\mathit{N}$ 個の要素)。

3. 監視関数に空間の平滑化を適用し、移動メッシュの方程式を評価します。

導関数の最初の $\mathit{N}$ 個の方程式は、Burger の方程式の右辺をエンコードします。Burger の方程式は、空間導関数を伴う次の形式の微分演算子とみなすことができます。

$\mathit{f}\left(\mathit{u}\right)=ϵ\frac{{\partial }^2\mathit{u}}{{\partial \mathit{x}}^2}-\frac{\partial }{\partial \mathit{x}}\left(\frac{{\mathit{u}}^2}{2}\right)$.

参考文献 [1] には、次による中心有限差分を使用した微分演算子 $\mathit{f}$ の近似手順が記載されています。

$${\mathit{f}}_{\mathit{i}}=ϵ\left[\frac{\left(\frac{{\mathit{u}}_{\mathit{i}+1}-{\mathit{u}}_{\mathit{i}}}{{\mathit{x}}_{\mathit{i}+1}-{\mathit{x}}_{\mathit{i}}}\right)-\left(\frac{{\mathit{u}}_{\mathit{i}}-{\mathit{u}}_{\mathit{i}-1}}{{\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{i}-1}}\right)}{\frac{1}{2}\left({\mathit{x}}_{\mathit{i}+1}-{\mathit{x}}_{\mathit{i}-1}\right)}\right]-\frac{1}{2}\left(\frac{{\mathit{u}}_{\mathit{i}+1}^2-{\mathit{u}}_{\mathit{i}-1}^2}{{\mathit{x}}_{\mathit{i}+1}-{\mathit{x}}_{\mathit{i}-1}}\right).$$

メッシュのエッジ ($\mathit{i}=1$ および $\mathit{i}=\mathit{N}$) では、代わりに片側差分のみが使用されます。この例では、$ϵ=1\times {10}^{-4}$ を使用します。

メッシュを扱う方程式 (導関数の最後の $\mathit{N}$ 個の方程式で構成) は次のとおりです。

$$\frac{{\partial }^2\dot{\mathit{x}}}{\partial {\mathit{t}}^2}=\frac{1}{\tau }\frac{\partial }{\partial \mathit{t}}\left(\mathit{B}\left(\mathit{x},\mathit{t}\right)\frac{\partial \mathit{x}}{\partial \mathit{t}}\right).$$

Burger の方程式と同様、有限差分を使用して監視関数 $\mathit{B}\left(\mathit{x},\mathit{t}\right)$ を近似できます。

$$\mathit{B}\left(\mathit{x},\mathit{t}\right)=\sqrt{1+{\left(\frac{\partial {\mathit{u}}_{\mathit{i}}}{\partial {\mathit{x}}_{\mathit{i}}}\right)}^2}=\sqrt{1+{\left(\frac{{\mathit{u}}_{\mathit{i}+1}-{\mathit{u}}_{\mathit{i}-1}}{{\mathit{x}}_{\mathit{i}+1}-{\mathit{x}}_{\mathit{i}-1}}\right)}^2}.$$

監視関数の評価後、空間の平滑化を適用します ([1] の方程式 14 と 15)。この例では、空間の平滑化パラメーターとして $\gamma =2$ と $\mathit{p}=2$ を使用します。

連立方程式をエンコードする関数は次のとおりです。

function g = movingMeshODE(t,y)
% Extract the components of y for the solution u and mesh x
N = length(y)/2;
u = y(1:N);
x = y(N+1:end);

% Boundary values of solution u and mesh x
u0 = 0;
uNP1 = 0;
x0 = 0;
xNP1 = 1;

% Preallocate g vector of derivative values.
g = zeros(2*N,1);

% Use centered finite differences to approximate the RHS of Burgers'
% equations (with single-sided differences on the edges). The first N
% elements in g correspond to Burgers' equations.
ind = 1:N;
x = [x0; x; xNP1];
u = [u0; u; uNP1];
i = 2:N+1;
delx = x(i+1) - x(i-1);
g(ind) = 1e-4*((u(i+1) - u(i))./(x(i+1) - x(i)) - ...
          (u(i) - u(i-1))./(x(i) - x(i-1)))./(0.5*delx) - ...
          0.5*(u(i+1).^2 - u(i-1).^2)./delx;

% Evaluate the monitor function values (Eq. 21 in reference paper), used in
% RHS of mesh equations. Centered finite differences are used for interior
% points, and single-sided differences are used on the edges.
M = zeros(N,1);
M(ind) = sqrt(1 + ((u(i+1) - u(i-1))./(x(i+1) - x(i-1))).^2);
M0 = sqrt(1 + ((u(2) - u0)/(x(2) - x0))^2);
MNP1 = sqrt(1 + ((uNP1 - u(N+1))/(xNP1 - x(N+1)))^2);

% Apply spatial smoothing (Eqns. 14 and 15) with gamma = 2, p = 2.
x = y(N+1:end);
ind = 2:N-1;
SM = zeros(N,1);
i = 3:N-2;
SM(i) = sqrt((4*M(i-2).^2 + 6*M(i-1).^2 + 9*M(i).^2 + ...
    6*M(i+1).^2 + 4*M(i+2).^2)/29);

SM0 = sqrt((9*M0^2 + 6*M(1)^2 + 4*M(2)^2)/19);
SM(1) = sqrt((6*M0^2 + 9*M(1)^2 + 6*M(2)^2 + 4*M(3)^2)/25);
SM(2) = sqrt((4*M0^2 + 6*M(1)^2 + 9*M(2)^2 + 6*M(3)^2 + 4*M(4)^2)/29);
SM(N-1) = sqrt((4*M(N-3)^2 + 6*M(N-2)^2 + 9*M(N-1)^2 + 6*M(N)^2 + 4*MNP1^2)/29);
SM(N) = sqrt((4*M(N-2)^2 + 6*M(N-1)^2 + 9*M(N)^2 + 6*MNP1^2)/25);
SMNP1 = sqrt((4*M(N-1)^2 + 6*M(N)^2 + 9*MNP1^2)/19);

g(ind+N) = (SM(ind+1) + SM(ind)).*(x(ind+1) - x(ind)) - ...
    (SM(ind) + SM(ind-1)).*(x(ind) - x(ind-1));
g(1+N) = (SM(2) + SM(1))*(x(2) - x(1)) - (SM(1) + SM0)*(x(1) - x0);
g(N+N) = (SMNP1 + SM(N))*(xNP1 - x(N)) - (SM(N) + SM(N-1))*(x(N) - x(N-1));

% Form final discrete approximation for Eq. 12 in reference paper, the equation governing
% the mesh points.
tau = 1e-3;
g(1+N:end) = - g(1+N:end)/(2*tau);
end

スパース パターン関数のコード化

導関数のヤコビアン $\mathrm{dF}/\mathrm{dy}$ は、導関数 movingMeshODE のすべての偏導関数を含む $2\mathit{N}\times 2\mathit{N}$ の行列です。この行列がオプション構造体に指定されていない場合、ode15s は有限差分を使用してヤコビアンを推定します。ヤコビアンのスパース パターンを指定することで、ode15s はより高速に計算できるようになります。

ヤコビアンのスパース パターン関数は次のとおりです。

function out = JPat(N)
S1 = spdiags(1,-1:1,N,N);
S2 = spdiags(1,-4:4,N,N);
out = [S1 S1; S2 S2];
end

spy を使用して、$\mathit{N}=80$ での $\mathrm{dF}/\mathrm{dy}$ のスパース パターンをプロットします。

spy(JPat(80))

計算を効率化するためのもう 1 つの方法は、$\mathit{d}\left(\mathrm{Mv}\right)/\mathrm{dy}$ のスパース パターンを指定することです。このスパース パターンは、${\mathit{u}}_{\mathit{i}}$ と ${\mathit{x}}_{\mathit{i}}$ のどの項が質量行列関数で計算された有限差分の中に存在するかを調べることで見出せます。

$\mathit{d}\left(\mathrm{Mv}\right)/\mathrm{dy}$ のスパース パターンの関数は次のとおりです。

function S = MvPat(N)
SZ = sparse(N,N);
S1 = spdiags(1,[-1 1],N,N);
S = [S1 S1; SZ SZ];
end

spy を使用して、$\mathit{N}=80$ での $\mathit{d}\left(\mathrm{Mv}\right)/\mathrm{dy}$ のスパース パターンをプロットします。

spy(MvPat(80))

連立方程式を解く

値 $\mathit{N}=80$ で連立方程式を解きます。初期条件については、等間隔グリッドで $\mathit{x}$ を初期化し、そのグリッド上で $\mathit{u}\left(\mathit{x},0\right)$ を評価します。

N = 80;
h = 1/(N+1);
xinit = h*(1:N);
uinit = sin(2*pi*xinit) + 0.5*sin(pi*xinit);
y0 = [uinit xinit];

odeset を使用して、いくつかの値を設定するオプション構造体を作成します。

• 質量行列の関数ハンドル

• 質量行列の状態依存。この問題では、質量行列は $\mathit{t}$ と $\mathit{y}$ の両方の関数であるため、'strong' となります。

• ヤコビ スパース パターンを計算する関数ハンドル

• ベクトルで乗算された質量行列の導関数のスパース パターンを計算する関数ハンドル

• 絶対許容誤差と相対許容誤差

opts = odeset(Mass=@mass,MStateDependence="strong",JPattern=JPat(N),...
    MvPattern=MvPat(N),RelTol=1e-5,AbsTol=1e-4);

最後に、導関数 movingMeshODE、時間範囲、初期条件、およびオプション構造体を使用して ode15s を呼び出し、区間 $\left[0,1\right]$ で連立方程式を解きます。

tspan = [0 1];
sol = ode15s(@movingMeshODE,tspan,y0,opts);

結果のプロット

積分の結果は、タイム ステップ $\mathit{t}$、メッシュ点 $\mathit{x}\left(\mathit{t}\right)$、解 $\mathit{u}\left(\mathit{x},\mathit{t}\right)$ を格納する構造体 sol となります。構造体からこれらの値を抽出します。

t = sol.x;
x = sol.y(N+1:end,:);
u = sol.y(1:N,:);

メッシュ点の経時的な動きをプロットします。プロットでは、時間経過に沿ってメッシュ点が適度に等間隔を保っていますが (監視関数による)、解の移動に伴い、解の不連続点近くでは密集しうることが示されています。

plot(x,t)
xlabel("t")
ylabel("x(t)")
title("Burgers' equation: Trajectories of grid points")

ここで、いくつかの $\mathit{t}$ の値で $\mathit{u}\left(\mathit{x},\mathit{t}\right)$ をサンプリングし、時間経過に伴う解の変化をプロットします。区間の両端のメッシュ点は固定で、x(0) = 0 と x(N+1) = 1 となっています。境界値は u(t,0) = 0 と u(t,1) = 0 であり、Figure 用に計算された既知の値として追加しなければなりません。

tint = 0:0.2:1;
yint = deval(sol,tint);
figure
labels = {};
for j = 1:length(tint)
   solution = [0; yint(1:N,j); 0];
   location = [0; yint(N+1:end,j); 1];
   labels{j} = ['t = ' num2str(tint(j))];
   plot(location,solution,"-o")
   hold on
end
xlabel("x")
ylabel("solution u(x,t)")
legend(labels{:},"Location","SouthWest")
title("Burgers equation on moving mesh")
hold off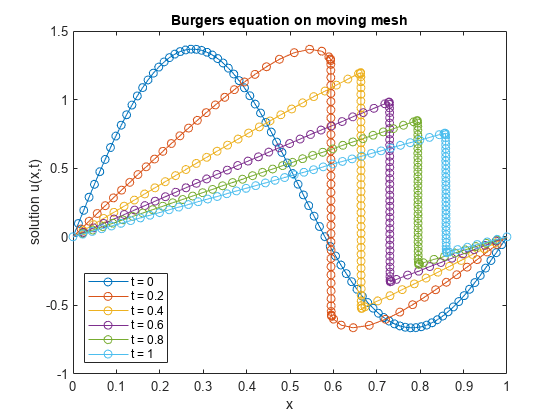

プロットは、$\mathit{u}\left(\mathit{x},0\right)$ が $\mathit{x}=1$ に向かって時間が経過するとともに急勾配が展開する、滑らかな波であることを示しています。メッシュ点は不連続点の動きを追跡するため、各タイム ステップで適切な位置に評価点が追加されています。

参照

[1] Huang, Weizhang, et al. “Moving Mesh Methods Based on Moving Mesh Partial Differential Equations.”Journal of Computational Physics, vol. 113, no. 2, Aug. 1994, pp. 279–90. https://doi.org/10.1006/jcph.1994.1135.

ローカル関数

ここでは、ソルバー ode15s が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function g = movingMeshODE(t,y)
% Extract the components of y for the solution u and mesh x
N = length(y)/2;
u = y(1:N);
x = y(N+1:end);

% Boundary values of solution u and mesh x
u0 = 0;
uNP1 = 0;
x0 = 0;
xNP1 = 1;

% Preallocate g vector of derivative values.
g = zeros(2*N,1);

% Use centered finite differences to approximate the RHS of Burgers'
% equations (with single-sided differences on the edges). The first N
% elements in g correspond to Burgers' equations.
ind = 1:N;
x = [x0; x; xNP1];
u = [u0; u; uNP1];
i = 2:N+1;
delx = x(i+1) - x(i-1);
g(ind) = 1e-4*((u(i+1) - u(i))./(x(i+1) - x(i)) - ...
          (u(i) - u(i-1))./(x(i) - x(i-1)))./(0.5*delx) - ...
          0.5*(u(i+1).^2 - u(i-1).^2)./delx;

% Evaluate the monitor function values (Eq. 21 in reference paper), used in
% RHS of mesh equations. Centered finite differences are used for interior
% points, and single-sided differences are used on the edges.
M = zeros(N,1);
M(ind) = sqrt(1 + ((u(i+1) - u(i-1))./(x(i+1) - x(i-1))).^2);
M0 = sqrt(1 + ((u(2) - u0)/(x(2) - x0))^2);
MNP1 = sqrt(1 + ((uNP1 - u(N+1))/(xNP1 - x(N+1)))^2);

% Apply spatial smoothing (Eqns. 14 and 15) with gamma = 2, p = 2.
x = y(N+1:end);
ind = 2:N-1;
SM = zeros(N,1);
i = 3:N-2;
SM(i) = sqrt((4*M(i-2).^2 + 6*M(i-1).^2 + 9*M(i).^2 + ...
    6*M(i+1).^2 + 4*M(i+2).^2)/29);

SM0 = sqrt((9*M0^2 + 6*M(1)^2 + 4*M(2)^2)/19);
SM(1) = sqrt((6*M0^2 + 9*M(1)^2 + 6*M(2)^2 + 4*M(3)^2)/25);
SM(2) = sqrt((4*M0^2 + 6*M(1)^2 + 9*M(2)^2 + 6*M(3)^2 + 4*M(4)^2)/29);
SM(N-1) = sqrt((4*M(N-3)^2 + 6*M(N-2)^2 + 9*M(N-1)^2 + 6*M(N)^2 + 4*MNP1^2)/29);
SM(N) = sqrt((4*M(N-2)^2 + 6*M(N-1)^2 + 9*M(N)^2 + 6*MNP1^2)/25);
SMNP1 = sqrt((4*M(N-1)^2 + 6*M(N)^2 + 9*MNP1^2)/19);

g(ind+N) = (SM(ind+1) + SM(ind)).*(x(ind+1) - x(ind)) - ...
    (SM(ind) + SM(ind-1)).*(x(ind) - x(ind-1));
g(1+N) = (SM(2) + SM(1))*(x(2) - x(1)) - (SM(1) + SM0)*(x(1) - x0);
g(N+N) = (SMNP1 + SM(N))*(xNP1 - x(N)) - (SM(N) + SM(N-1))*(x(N) - x(N-1));

% Form final discrete approximation for Eq. 12 in reference paper, the equation governing
% the mesh points.
tau = 1e-3;
g(1+N:end) = - g(1+N:end)/(2*tau);
end

% -----------------------------------------------------------------------
function M = mass(t,y)
% Extract the components of y for the solution u and mesh x
N = length(y)/2; 
u = y(1:N);
x = y(N+1:end);

% Boundary values of solution u and mesh x
u0 = 0;
uNP1 = 0;
x0 = 0;
xNP1 = 1;

% M1 and M2 are the portions of the mass matrix for Burgers' equation. 
% The derivative du/dx is approximated with finite differences, using 
% single-sided differences on the edges and centered differences in between.
M1 = speye(N);
i = 2:N-1;
v = [0; -(u(i+1) - u(i-1))./(x(i+1) - x(i-1)) ; 0];
M2 = spdiags(v,0,N,N);

M2(1,1) = - (u(2) - u0)/(x(2) - x0);
M2(N,N) = - (uNP1 - u(N-1))/(xNP1 - x(N-1));

% M3 and M4 define the equations for mesh point evolution, corresponding to 
% MMPDE6 in the reference paper. Since the mesh functions only involve d/dt(dx/dt), 
% the M3 portion of the mass matrix is all zeros. The second derivative in M4 is 
% approximated using a finite difference Laplacian matrix. 
M3 = sparse(N,N);
M4 = spdiags([1 -2 1],-1:1,N,N);

% Assemble mass matrix
M = [M1 M2; M3 M4];
end

% -------------------------------------------------------------------------
function out = JPat(N)  % Jacobian sparsity pattern
S1 = spdiags(1,-1:1,N,N);
S2 = spdiags(1,-4:4,N,N);
out = [S1 S1; S2 S2];
end

% -------------------------------------------------------------------------
function S = MvPat(N)  % Sparsity pattern for the derivative of the Mass matrix times a vector
SZ = sparse(N,N);
S1 = spdiags(1,[-1 1],N,N);
S = [S1 S1; SZ SZ];
end
% -------------------------------------------------------------------------

参考

ode15s | odeset

トピック

• ODE ソルバーの選択
• ODE オプションの概要
• 空中に投げられたバトンの動きを表す方程式の求解