空中に投げられたバトンの動きを表す方程式の求解

ライブスクリプトを開く

この例では、空中に投げられたバトンのダイナミクスをモデル化する連立常微分方程式を解きます [1]。バトンは、長さ $L$ のロッドで結合された質量 $m_{1}$ および $m_{2}$ の 2 つの質点としてモデル化されます。バトンは空中に投げられた後、重力の影響を受けながら、垂直な xy 平面内を移動します。ロッドは水平方向と $θ$ の角度をもち、1 つ目の質点の座標は $(x, y)$ です。この定式化では、2 つ目の質点の座標は $(x + L \cos θ, y + L \sin θ)$ です。

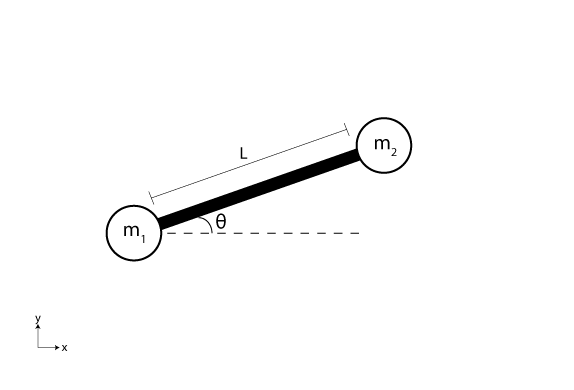
このシステムの運動方程式は、3 つの座標 $x$ 、 $y$ 、および $θ$ それぞれに対しラグランジュ方程式を適用することで得られます。

$\begin{array}{l} (m_{1} + m_{2}) \ddot{x} - m_{2} L \ddot{θ} \sin θ - m_{2} L {\dot{θ}}^{2} \cos θ = 0, \\ (m_{1} + m_{2}) \ddot{y} - m_{2} L \ddot{θ} \cos θ - m_{2} L {\dot{θ}}^{2} \sin θ + (m_{1} + m_{2}) g = 0, \\ L^{2} \ddot{θ} - L \ddot{x} \sin θ + L \ddot{y} \cos θ + g L \cos θ = 0 . \end{array}$

方程式のコード作成

MATLAB では、 $\dot{q} = f (t, q)$ の形式で方程式を記述する必要があります。ここで、 $\dot{q}$ は各座標の 1 階微分です。この問題では、解ベクトルに $x$ 、 $y$ 、角度 $θ$ 、およびそれらの 1 階微分という 6 つの要素があります。

$q = [\begin{array}{c} q_{1} \\ q_{2} \\ q_{3} \\ q_{4} \\ q_{5} \\ q_{6} \end{array}] = [\begin{array}{c} x \\ \dot{x} \\ y \\ \dot{y} \\ θ \\ \dot{θ} \end{array}] .$

この表記を使って、運動方程式全体を $q$ の要素によって書き換えることができます。

$\begin{array}{l} (m_{1} + m_{2}) \dot{q_{2}} - m_{2} L \dot{q_{6}} \sin q_{5} = m_{2} L q_{6}^{2} \cos q_{5}, \\ (m_{1} + m_{2}) \dot{q_{4}} - m_{2} L \dot{q_{6}} \cos q_{5} = m_{2} L q_{6}^{2} \sin q_{5} - (m_{1} + m_{2}) g, \\ L^{2} \dot{q_{6}} - L \dot{q_{2}} \sin q_{5} + L \dot{q_{4}} \cos q_{5} = - g L \cos q_{5} . \end{array}$

左辺に 1 階微分の項がいくつか存在するため、残念ながらこの運動方程式はソルバーが必要とする形式 $\dot{q} = f (t, q)$ に適合しません。こうした場合は、質量行列を使用して方程式の左辺を表現しなければなりません。

行列表記では、 $M (t, q) \dot{q} = f (t, q)$ の形式で質量行列を使用して、6 つの方程式からなる方程式系として運動方程式を書き換えることができます。質量行列では、方程式の左辺にある 1 階微分の線形結合が、行列とベクトルの積により表現されます。この形式では、方程式系は次のようになります。

$[\begin{array}{c} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & m_{1} + m_{2} & 0 & 0 & 0 & - m_{2} L \sin q_{5} \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & m_{1} + m_{2} & 0 & m_{2} L \cos q_{5} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & - L \sin q_{5} & 0 & L \cos q_{5} & 0 & L^{2} \end{array}] [\begin{array}{c} \dot{q_{1}} \\ \dot{q_{2}} \\ \dot{q_{3}} \\ \dot{q_{4}} \\ \dot{q_{5}} \\ \dot{q_{6}} \end{array}] = [\begin{array}{c} q_{2} \\ m_{2} L q_{6}^{2} \cos q_{5} \\ q_{4} \\ m_{2} L q_{6}^{2} \sin q_{5} - (m_{1} + m_{2}) g \\ q_{6} \\ - g L \cos q_{5} \end{array}]$

この式から、質量行列の非ゼロ要素を計算する関数を記述できます。関数は 3 つの入力を取ります。 $t$ と解ベクトル $q$ は必須 (関数本体で使用されない場合でも、これらの入力を指定しなければなりません) であり、 $P$ はオプションの追加入力で、パラメーター値を渡すために使用されます。

function M = mass(t,q,P)
% Extract parameters
m1 = P(1);
m2 = P(2);
L = P(3);
g = P(4);

% Mass matrix elements
M = zeros(6,6);
M(1,1) = 1;
M(2,2) = m1 + m2;
M(2,6) = -m2*L*sin(q(5));
M(3,3) = 1;
M(4,4) = m1 + m2;
M(4,6) = m2*L*cos(q(5));
M(5,5) = 1;
M(6,2) = -L*sin(q(5));
M(6,4) = L*cos(q(5));
M(6,6) = L^2;
end

次に、方程式系 $M (t, q) \dot{q} = f (t, q)$ における各方程式の右辺の関数を記述できます。質量行列関数と同様、この関数は $t$ と $q$ という 2 つの必須入力と、パラメーター値 $P$ という 1 つのオプション入力を取ります。

function dydt = f(t,q,P)
% Extract parameters
m1 = P(1);
m2 = P(2);
L = P(3);
g = P(4);

% Equations to solve
dydt = [q(2)
        m2*L*q(6)^2*cos(q(5))
        q(4)
        m2*L*q(6)^2*sin(q(5))-(m1+m2)*g
        q(6)
        -g*L*cos(q(5))];
end

方程式を解く

まず、 $m_{1}$ 、 $m_{2}$ 、 $L$ 、および $g$ のパラメーター値からなるベクトル P を作成します。ソルバーはベクトル P を追加入力として質量行列と ODE 関数に渡します。

P = [0.1 0.1 1 9.81];

問題の初期条件のベクトルを作成します。バトンはある角度で上向きに投げられるため、初期速度には非ゼロ値を $\dot{x_{0}} = 4$ 、 $\dot{y_{0}} = 20$ 、 $\dot{θ_{0}} = 2$ のように使用します。バトンは直立位置からの開始となるため、初期位置は $θ_{0} = - π / 2$ 、 $x_{0} = 0$ 、 $y_{0} = L$ となります。

y0 = [0; 4; P(3); 20; -pi/2; 2];

次に、問題を表す ode オブジェクトを作成し、ODEFcn、MassMatrix、InitialValue、および Parameters の値を指定します。オブジェクトの表示から、この問題のソルバーとして ode15s が選択されていることがわかります。質量行列があるためです。

F = ode(ODEFcn=@f,...
        MassMatrix=@mass,...
        InitialValue=y0,...
        Parameters=P)

F = 
  ode with properties:

   Problem definition
               ODEFcn: @f
           Parameters: [0.1000 0.1000 1 9.8100]
          InitialTime: 0
         InitialValue: [6x1 double]
             Jacobian: []
           MassMatrix: [1x1 odeMassMatrix]
         EquationType: standard

   Solver properties
    AbsoluteTolerance: 1.0000e-06
    RelativeTolerance: 1.0000e-03
               Solver: auto
       SelectedSolver: ode15s

  Show all properties

積分の時間範囲として 0 ～ 4 の 25 点からなるベクトルを作成し、solve を使用して方程式系をシミュレートします。時間のベクトルを指定すると、ソルバーは独自の内部ステップを取りますが、指定された時点における解を内挿します。

tspan = linspace(0,4,25);
sol = solve(F,tspan)

sol = 
  ODEResults with properties:

        Time: [0 0.1667 0.3333 0.5000 0.6667 0.8333 1 1.1667 1.3333 1.5000 1.6667 1.8333 2 2.1667 2.3333 2.5000 2.6667 2.8333 3 3.1667 3.3333 3.5000 3.6667 3.8333 4]
    Solution: [6x25 double]

結果のプロット

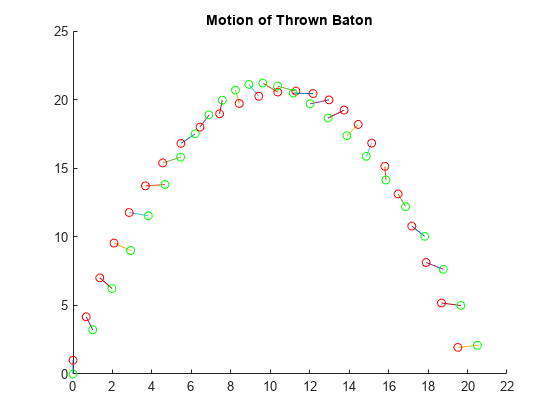
solve からの出力には、要求された各タイムステップでの運動方程式の解が含まれます。結果を確認するために、時間経過に沿ったバトンの運動をプロットします。

解の各列をループし、タイムステップごとにバトンの位置をプロットします。時間経過に沿った回転が確認できるよう、バトンのそれぞれの端に色を付けます。

figure
title("Motion of Thrown Baton");
axis([0 22 0 25])
hold on
for j = 1:length(sol.Time)
   theta = sol.Solution(5,j);
   X = sol.Solution(1,j);
   Y = sol.Solution(3,j);
   xvals = [X X+P(3)*cos(theta)];
   yvals = [Y Y+P(3)*sin(theta)];
   plot(xvals,yvals,xvals(1),yvals(1),"ro",xvals(2),yvals(2),"go")
end
hold off

Figure contains an axes object. The axes object with title Motion of Thrown Baton contains 75 objects of type line. One or more of the lines displays its values using only markers

参照

[1] Wells, Dare A. Schaum’s Outline of Theory and Problems of Lagrangian Dynamics: With a Treatment of Euler’s Equations of Motion, Hamilton’s Equations and Hamilton’s Principle. Schaum's Outline Series. New York: Schaum Pub. Co, 1967.

参考

ode45

空中に投げられたバトンの動きを表す方程式の求解

方程式のコード作成

方程式を解く

結果のプロット

参照

参考

関連するトピック