高次のソルバーを使用した天体力学問題の求解

この例では、ode78 および ode89 を使用して、積分の成功のために ODE ソルバーの各ステップで高い精度が要求される天体力学問題を解く方法を説明します。ode45 と ode113 はどちらも、既定の許容誤差を使用してこの問題を解くことができません。誤差のしきい値がより厳密である場合でも、ode89 は各ステップで使用するルンゲ・クッタ公式の精度が高いため、この問題に最適です。

問題の説明

"プレアデス問題" は、7 つの星の重力相互作用を示す天体力学問題です [1]。この星団は "セブン シスターズ" とも呼ばれ、地球に近いため夜空で肉眼で見えます [2]。この星団の星の動きを記述する方程式系は、14 個のノンスティッフ 2 階微分方程式で構成され、1 階形式で書き換えると 28 個の方程式の系が得られます。

ニュートンの運動の第 2 法則は、物体に加えられる力とその運動量の経時変化率を関連付けるものです。

${\mathit{F}}_{\mathit{i}}=\frac{\mathrm{d}}{\mathrm{d}\mathit{t}}{\mathit{p}}_{\mathit{i}}$.

運動量 (${\mathit{p}}_{\mathit{i}}={\mathit{m}}_{\mathit{i}}{\mathit{v}}_{\mathit{i}}$) には、個別の "x" 成分と "y" 成分があります。同時に、万有引力の法則は、次のように物体 "j" から物体 "i" に作用する力について説明するものです。

${\mathit{F}}_{\mathrm{ij}}=\mathit{g}\frac{{\mathit{m}}_{\mathit{i}}{\mathit{m}}_{\mathit{j}}}{{\Vert {\mathit{p}}_{\mathit{i}}-{\mathit{p}}_{\mathit{j}}\Vert }^2}{\mathit{d}}_{\mathrm{ij}}$.

項 ${\mathit{d}}_{\mathrm{ij}}=\frac{{\mathit{p}}_{\mathit{j}}-{\mathit{p}}_{\mathit{i}}}{\Vert {\mathit{p}}_{\mathit{j}}-{\mathit{p}}_{\mathit{i}}\Vert }$ は物体間の距離の方向を示し、物体の質量は ${\mathit{m}}_{\mathit{i}}=\mathit{i}$ ($\mathit{i}=1,2,...,7$) です。多くの物体を含む系では、個々の物体に加えられる力はその他すべてとの相互作用の合計であるため、次のようになります。

$${\mathit{F}}_{\mathit{i}}=\sum _{\mathit{i}\ne \mathit{j}}{\mathit{F}}_{\mathrm{ij}}.$$

重力定数 $\mathit{g}$ を 1 と等しくなるよう設定して解を求めると、"x" 成分と "y" 成分の経時変化を記述する 2 次方程式系が得られます。

$${{{\mathit{x}}_{\mathit{i}}}^{\prime }}^{\prime }={\mathit{f}}_{\mathit{i}}\left(\mathit{x},\mathit{y}\right)=\sum _{\mathit{j}\ne \mathit{i}}\frac{{\mathit{m}}_{\mathit{j}}\left({\mathit{x}}_{\mathit{j}}-{\mathit{x}}_{\mathit{i}}\right)}{{\mathit{r}}_{\mathrm{ij}}^{3/2}},$$

$${{{\mathit{y}}_{\mathit{i}}}^{\prime }}^{\prime }={\mathit{h}}_{\mathit{i}}\left(\mathit{x},\mathit{y}\right)=\sum _{\mathit{j}\ne \mathit{i}}\frac{{\mathit{m}}_{\mathit{j}}\left({\mathit{y}}_{\mathit{j}}-{\mathit{y}}_{\mathit{i}}\right)}{{\mathit{r}}_{\mathrm{ij}}^{3/2}},$$

ここで ${\mathit{r}}_{\mathrm{ij}}=\sqrt{{\left({\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{j}}\right)}^2+{\left({\mathit{y}}_{\mathit{i}}-{\mathit{y}}_{\mathit{j}}\right)}^2}$ です。これら 2 つの方程式が系内の 7 つの星それぞれに適用されるため、14 個の 2 階微分方程式 ($\mathit{i}=1,2,...,7)$ が系全体を記述します。

[1] に記載されているように、方程式系の初期条件は次のとおりです。

$$\{\begin{array}{cc}{x}_0& =(3,3,-1,-3,2,-2,2)\\ y_0& =(3,-3,2,0,0,-4,4)\\ x_0^{\prime }& =(0,0,0,0,0,1.75,-1.5)\\ y_0^{\prime }& =(0,0,0,-1.25,1,0,0)\end{array}$$

MATLAB® でこの ODE 系を解くには、ソルバー ode78 とソルバー ode89 を呼び出す前に方程式を関数へとコード化する必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード作成

MATLAB の ODE ソルバーでは、方程式を 1 次形式 ${\mathit{q}}^{\prime }=\mathit{u}\left(\mathit{t},\mathit{q}\right)$ で記述する必要があります。この問題では、代入 $\mathit{w}={\mathit{x}}^{\prime }$ および $\mathit{z}={\mathit{y}}^{\prime }$ を使用してこの方程式系を 1 次形式で書き換えることができます。これらの代入を使用すると、この方程式系には 28 個の 1 次方程式が含まれ、7 つの方程式からなる 4 つのグループに整理されます。

$$\left[\begin{array}{c}{x}_i^{\prime }\\ y_i^{\prime }\\ w_i^{\prime }\\ z_i^{\prime }\end{array}\right]=\left[\begin{array}{c}{w}_i\\ z_i\\ f_i(x,y)\\ h_i(x,y)\end{array}\right]$$.

この方程式系を解くことで得られる解ベクトルの形式は次のとおりです。

$$\mathit{q}=\left[\begin{array}{c}{\mathit{x}}_{\mathit{i}}\\ {\mathit{y}}_{\mathit{i}}\\ {\mathit{w}}_{\mathit{i}}\\ {\mathit{z}}_{\mathit{i}}\end{array}\right].$$

したがって、解ベクトル $\mathit{q}$ に基づいて元の方程式を記述すると、次のようになります。

$$\left[\begin{array}{c}{{\mathit{x}}_{\mathit{i}}}^{\prime }\\ {{\mathit{y}}_{\mathit{i}}}^{\prime }\\ {{\mathit{w}}_{\mathit{i}}}^{\prime }\\ {{\mathit{z}}_{\mathit{i}}}^{\prime }\end{array}\right]=\left[\begin{array}{c}\left({\mathit{q}}_{15},{\mathit{q}}_{16},...,{\mathit{q}}_{21}\right)\\ \left({\mathit{q}}_{22},{\mathit{q}}_{23},...,{\mathit{q}}_{28}\right)\\ {\mathit{f}}_{\mathit{i}}\left(\mathit{x},\mathit{y}\right)\\ {\mathit{h}}_{\mathit{i}}\left(\mathit{x},\mathit{y}\right)\end{array}\right],$$

ここで $\mathit{x}=\left({\mathit{q}}_1,{\mathit{q}}_2,...,{\mathit{q}}_7\right)$ および $\mathit{y}=\left({\mathit{q}}_8,{\mathit{q}}_9,...,{\mathit{q}}_{14}\right)$ です。1 次形式 ${\mathit{q}}^{\prime }=\mathit{u}\left(\mathit{t},\mathit{q}\right)$ で記述された方程式を使用すると、解法プロセスの各タイム ステップで成分を計算する関数を記述できます。この方程式系をコード化する関数は次のとおりです。

function dqdt = pleiades(t,q)
  x = q(1:7);
  y = q(8:14);
  xDist = (x - x.');
  yDist = (y - y.');
  r = (xDist.^2+yDist.^2).^(3/2);
  m = (1:7)';
  dqdt = [q(15:28);
          sum(xDist.*m./r,1,'omitnan').';
          sum(yDist.*m./r,1,'omitnan').'];
end

この関数では、$\mathit{x}$ と $\mathit{y}$ の値は解ベクトル $\mathit{q}$ から直接抽出され、出力の最初の 14 個の成分も同様です。次に、この関数は位置の値を使用して 7 つすべての星の間の距離を計算し、これらの距離が ${\mathit{f}}_{\mathit{i}}\left(\mathit{x},\mathit{y}\right)$ および ${\mathit{h}}_{\mathit{i}}\left(\mathit{x},\mathit{y}\right)$ のコードで使用されます。

オプション パラメーターの設定

関数 odeset を使用して、いくつかのオプション パラメーターの値を設定します。

• 相対許容誤差と絶対許容誤差として、それぞれ厳しい許容誤差 1e-13 および 1e-15 を指定します。

• ソルバー統計の表示をオンにします。

opts = odeset("RelTol",1e-13,"AbsTol",1e-15,"Stats","on");

方程式を解く

初期条件をもつ列ベクトルと、範囲 $\left[0,15\right]$ の等間隔の点をもつ時間ベクトルを作成します。2 つを超える要素をもつ時間ベクトルを指定すると、ソルバーは指定された時間点における解を返します。

init = [3 3 -1 -3 2 -2 2 ...
        3 -3 2 0 0 -4 4 ...
        0 0 0 0 0 1.75 -1.5 ...
        0 0 0 -1.25 1 0 0]';
tspan = linspace(1,15,200);

ここで、ode78 と ode89 の両方を使用して、方程式、時間範囲、初期値、およびオプションを指定して方程式を解きます。tic と toc を使用して、比較のために各ソルバーの時間を測定します (時間測定値は使用するコンピューターによって異なる場合があることに注意してください)。

tic
[t78,q78] = ode78(@pleiades,tspan,init,opts);

14963 successful steps
549 failed attempts
201899 function evaluations

toc

Elapsed time is 5.194569 seconds.

tic
[t89,q89] = ode89(@pleiades,tspan,init,opts);

4181 successful steps
56 failed attempts
68726 function evaluations

toc

Elapsed time is 2.554040 seconds.

この出力は、ode89 の方が高速で、失敗したステップが少ないため、問題を解くうえで最適であることを示しています。

解の曲線のプロット

q89 の最初の 14 個の成分には、ode89 で得られた 7 つの星それぞれの "x" と "y" の位置が含まれています。これらの解要素をプロットして、時間の経過に伴うすべての星の軌跡を確認します。

plot(q89(:,1),q89(:,8),'--',...
     q89(:,2),q89(:,9),'--',...
     q89(:,3),q89(:,10),'--',...
     q89(:,4),q89(:,11),'--',...
     q89(:,5),q89(:,12),'--',...
     q89(:,6),q89(:,13),'--',...
     q89(:,7),q89(:,14),'--')
title('Position of Pleiades Stars, Solved by ODE89')
xlabel('X Position')
ylabel('Y Position')

結果のアニメーションの作成

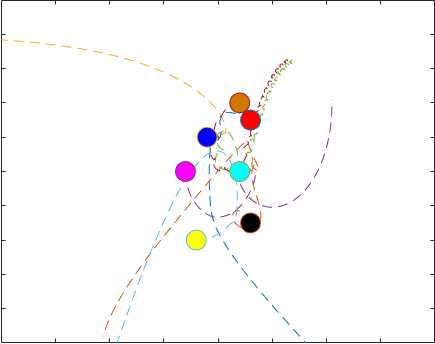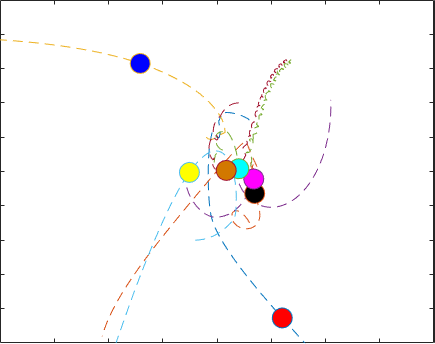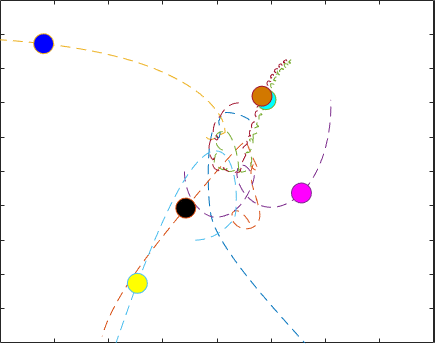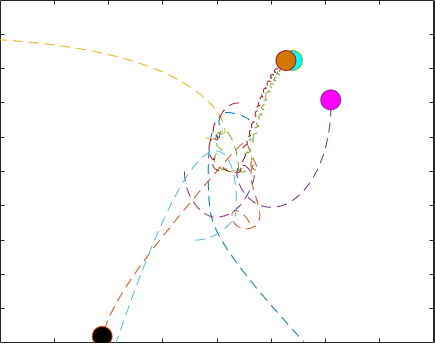
星の軌跡は大きくオーバーラップしているため、結果を可視化するには、星の経時的な動きを示すアニメーションを作成することをお勧めします。この例の最後にローカル関数として記載されている関数 AnimateOrbits は、この問題のソルバーからの出力を受け入れ、星がその軌跡に沿って移動することを示すアニメーション GIF ファイルを現在のフォルダーに作成します。

たとえば、次のコマンドを使用して ode89 ソルバーからの出力でアニメーションを生成できます。

AnimateOrbits(t89,q89);

以下はサンプルの出力 GIF です。

参照

[1] Hairer, E., et al. "Solving Ordinary Differential Equations I: Nonstiff Problems". 2nd rev. ed, Springer, 2009.

[2] "Pleiades." "Wikipedia", 21 June 2021. "Wikipedia", https://en.wikipedia.org/wiki/Pleiades.

ローカル関数

この節では、ODE ソルバーが解を計算するために呼び出すローカル関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function dqdt = pleiades(t,q)
  x = q(1:7);
  y = q(8:14);
  xDist = (x - x.');
  yDist = (y - y.');
  r = (xDist.^2+yDist.^2).^(3/2);
  m = (1:7)';
  dqdt = [q(15:28);
          sum(xDist.*m./r,1,'omitnan').';
          sum(yDist.*m./r,1,'omitnan').'];
end
%-----------------------------------------------------------------
function AnimateOrbits(t,q)
for k = 1:length(t)
    plot(q(:,1),q(:,8),'--',q(:,2),q(:,9),'--',...
         q(:,3),q(:,10),'--',q(:,4),q(:,11),'--',...
         q(:,5),q(:,12),'--',q(:,6),q(:,13),'--',...
         q(:,7),q(:,14),'--')
    hold on
    xlim([-20 20])
    ylim([-10 10])
    sz = 15;
    plot(q(k,1),q(k,8),'o','MarkerSize',sz,'MarkerFaceColor','r')
    plot(q(k,2),q(k,9),'o','MarkerSize',sz,'MarkerFaceColor','k')
    plot(q(k,3),q(k,10),'o','MarkerSize',sz,'MarkerFaceColor','b')
    plot(q(k,4),q(k,11),'o','MarkerSize',sz,'MarkerFaceColor','m')
    plot(q(k,5),q(k,12),'o','MarkerSize',sz,'MarkerFaceColor','c')
    plot(q(k,6),q(k,13),'o','MarkerSize',sz,'MarkerFaceColor','y')
    plot(q(k,7),q(k,14),'o','MarkerSize',sz,'MarkerFaceColor',[210 120 0]./255)
    hold off
    drawnow
    M(k) = getframe(gca);
    im{k} = frame2im(M(k));
end

filename = "orbits.gif";
for idx = 1:length(im)
    [A,map] = rgb2ind(im{idx},256);
    if idx == 1
        imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0);
    else
        imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0);
    end
end
close all
end

参考

ode78 | ode89 | odeset

関連するトピック

• ODE ソルバーの選択
• ODE オプションの概要
• 空中に投げられたバトンの動きを表す方程式の求解