このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

地上局アクセスの制約を満たしながら衛星群を最適化する

この例では、Global Optimization Toolbox ソルバーと Aerospace Toolbox ™ 関数を使用して、地上局のアクセス要件を満たす最小限の衛星コンステレーションを見つける方法を示します。この例では、4 つの局からなる地上局ネットワークが与えられていることを前提としています。より複雑な最適化には、衛星だけでなく地上局の割り当ても含まれる可能性があります。アクセス要件は次のとおりです。

• いくつかの関心地点は、少なくとも一定の割合の時間、衛星から観測可能でなければなりません。この例では、関心のあるポイントは地上局です。

• 各衛星は、データをダウンロードするために、少なくとも一定の割合の時間、地上局を監視する必要があります。これらのパーセンテージは、accessPercentage (Aerospace Toolbox) 関数を使用して計算できます。

すべての衛星は同じ高度にあり、高度は最適化変数の 1 つです。衛星は同じ軌道傾斜角にあり、これも最適化の変数です。衛星は、10 以下の整数である最適化変数である多数の軌道面にあります。最後に、軌道面あたりの衛星数は最適化変数であり、20 以下の整数です。

目的は衛星の総数を最小限に抑えることです。

星座の定義

ワークスペースに 4 つの地上局の座標を配置します。地上局を地図上にプロットします。

targets = table(...
    Size=[0,3],...
    VariableTypes=["string","double","double"],...
    VariableNames=["Name","Latitude","Longitude"]);

targets(1:4,:) = {...
    "Paris",        48.856614,      2.3522219  ;
    "Bruxelles",    50.850340,      4.351710   ;
    "Kiruna",       64.8557995,     20.2252821 ;    % Far from the equator
    "Kourou",       5.1597,         -52.6503  };    % Close to the equator
figure;
geoaxes("Basemap","satellite");
geoplot(targets.Latitude, targets.Longitude,"ko",MarkerFaceColor="red");
% Annotate the targets.
text(targets.Latitude,targets.Longitude,targets.Name,FontWeight="bold");

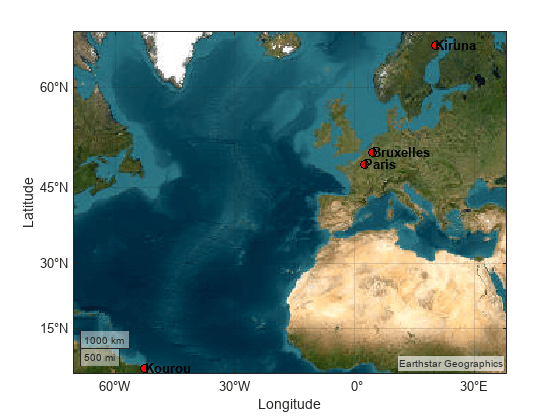
地上局は、少なくとも 1 つの衛星によって、少なくとも minObservability = 90% の時間にわたって観測可能でなければなりません。この制約が星座に対して満たされているかどうかを計算するには、この例の最後にある observability ヘルパー関数を使用します。この関数は、衛星シナリオ関数 walkerDelta (Aerospace Toolbox) と Aerospace Toolbox で使用可能なアクセス メソッドを使用します。

minObservability = 0.9;

衛星シナリオを定義し、指定されたターゲットを地上局として含めます。シナリオとターゲット オブジェクトを mission という名前の構造にバンドルします。

% Setup scenario
mission.Scenario = satelliteScenario(...
    datetime(2023,09,02,12,0,0),...
    datetime(2023,09,02,12,0,0) + days(1),...
    300);

% Ground stations
mission.Targets = groundStation(...
    mission.Scenario,...
    Name=targets.Name,...
    Latitude=targets.Latitude,...
    Longitude=targets.Longitude,...
    MinElevationAngle=30);

衛星群の定義の一部となるいくつかの量を定義します。詳細は、walkerDelta (Aerospace Toolbox)を参照してください。

phasing = 0;
argLat = 15; % deg

最適化問題の定義

この問題を最適化問題として定式化するには、最適化変数を定義し、次にこれらの変数に基づいて制約と目的関数を定義します。最適化問題を設定するための使いやすいインターフェースを提供する 問題ベースの最適化ワークフロー を使用します。

最適化変数

最適化問題には次の変数を使用します。

• numPlanes — 軌道面の数、1 から 10 までの整数。

• satPerPlane — 軌道面あたりの衛星数。1 から 20 までの整数。

• inclination — 傾斜度数、40 から 80 までの実数スカラー。

• altitude — メガメートル単位の高度、0.5 から 1.2 までの実数スカラー。この変数を他の変数とほぼ同じスケールにするには、一般的なキロメートルやメートルの代わりにメガメートルを使用します。この例の最後にある alt2radius ヘルパー関数は、高さをメガメートルからメートルに変換し、地球の半径を変換に含めます。

optimvar 関数を使用して最適化変数を定義します。変数の型 (記載されている場合は整数または連続) と境界を含めます。

numPlanes = optimvar("numPlanes",Type="integer",LowerBound=1,UpperBound=10);
satPerPlane = optimvar("satPerPlane",Type="integer",LowerBound=1,UpperBound=20);
inclination = optimvar("inclination",LowerBound=40,UpperBound=80);
altitude = optimvar("altitude",LowerBound=0.5,UpperBound=1.2);

目的関数

目的は、衛星の数、つまり軌道面あたりの衛星の数と軌道面の数を掛け合わせた数を最小限に抑えることです。

$$\mathrm{minimize}\mathrm{satPerPlane}*\mathrm{numPlanes}$$

この最小化の目的関数を含む最適化問題を作成します。

satelliteProb = optimproblem(Objective=satPerPlane*numPlanes,ObjectiveSense="minimize");

制約

この問題の制約は

$\mathrm{visibility}\ge \mathrm{minObservability}$

可視性は変数の複雑な関数です。この例の最後にある observability ヘルパー関数がこの量を計算します。このヘルパー関数を問題に配置するには、fcn2optimexpr 関数を使用して関数を最適化式に変換します。

visibility = fcn2optimexpr(@observability,numPlanes,satPerPlane,mission,...
                altitude,inclination,phasing,argLat);

最適化問題に制約を追加します。

satelliteProb.Constraints = visibility >= minObservability;

問題を確認します。

show(satelliteProb)

  OptimizationProblem : 

	Solve for:
       altitude, inclination, numPlanes, satPerPlane
	where:
       numPlanes, satPerPlane integer

	minimize :
       satPerPlane*numPlanes


	subject to :
       arg_LHS >= arg_RHS

       where:

             arg1 = observability(numPlanes, satPerPlane, extraParams{1}, altitude, inclination, 0, 15);
             arg_LHS = arg1;
             arg2 = 0.9;
             arg1 = arg2(ones(1,4));
             arg_RHS = arg1(:);

       extraParams

	variable bounds:
       0.5 <= altitude <= 1.2

       40 <= inclination <= 80

       1 <= numPlanes <= 10

       1 <= satPerPlane <= 20

問題を解く

問題の定式化は完了です。問題を解決するために使用できるソルバーを特定します。

[default,available] = solvers(satelliteProb)

default = 
"ga"

available = 1×3 string
    "ga"    "surrogateopt"    "gamultiobj"

このような時間のかかる整数制約の問題の場合、デフォルトの ga よりも surrogateopt ソルバーの方が効率的であることがよくあります。

surrogateopt ソルバーを使用して問題を解きます。ソリューションの進行状況を監視するには、optimplotfvalconstr プロット関数を指定します。より高速なソリューションを試すには、並列コンピューティングを指定します (Parallel Computing Toolbox ™ が必要)。より優れた代替モデルを取得するには、MinSurrogatePoints オプションをデフォルト値の 2 倍である 40 に設定します。また、関数評価の最大回数をデフォルト値より 100 多い 300 に設定します。並列で実行すると、surrogateopt は再現可能な結果を生成しません。したがって、実行環境がシリアルの場合は、再現可能な結果を得るためにランダム シードを設定します。

rng default % For reproducibility
options = optimoptions("surrogateopt",PlotFcn=@optimplotfvalconstr,...
    UseParallel=true,MaxFunctionEvaluations=300,MinSurrogatePoints=40);
[sol,fval,exitflag,output] = solve(satelliteProb,Solver="surrogateopt",Options=options)

Solving problem using surrogateopt.

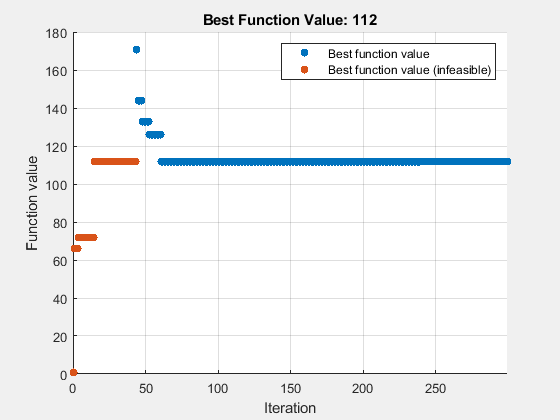
surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = struct with fields:
       altitude: 1.2000
    inclination: 62.8358
      numPlanes: 7
    satPerPlane: 16

fval = 112

exitflag = 
    SolverLimitExceeded

output = struct with fields:
        elapsedtime: 4.9507e+03
          funccount: 300
    constrviolation: 3.4602e-04
               ineq: [-0.1000 -0.1000 -0.1000 3.4602e-04]
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'
             solver: 'surrogateopt'

ディスプレイソリューション

最適化ソリューションから個別の変数を取得します。

numPlanes = sol.numPlanes

numPlanes = 7

numSatPerPlane = sol.satPerPlane

numSatPerPlane = 16

altitudeMm = sol.altitude

altitudeMm = 1.2000

inclination = sol.inclination

inclination = 62.8358

disp("Total number of satellites: " + evaluate(satelliteProb.Objective,sol))

Total number of satellites: 112

衛星群を視覚化します。

radiusMeters = alt2radius(altitudeMm);

mission.Constellation = walkerDelta(...
    mission.Scenario,...
    radiusMeters,...
    inclination,...
    numSatPerPlane*numPlanes,...
    numPlanes,...
    phasing,...
    ArgumentOfLatitude=argLat,...
    Name="Sat");

satelliteScenarioViewer(mission.Scenario);

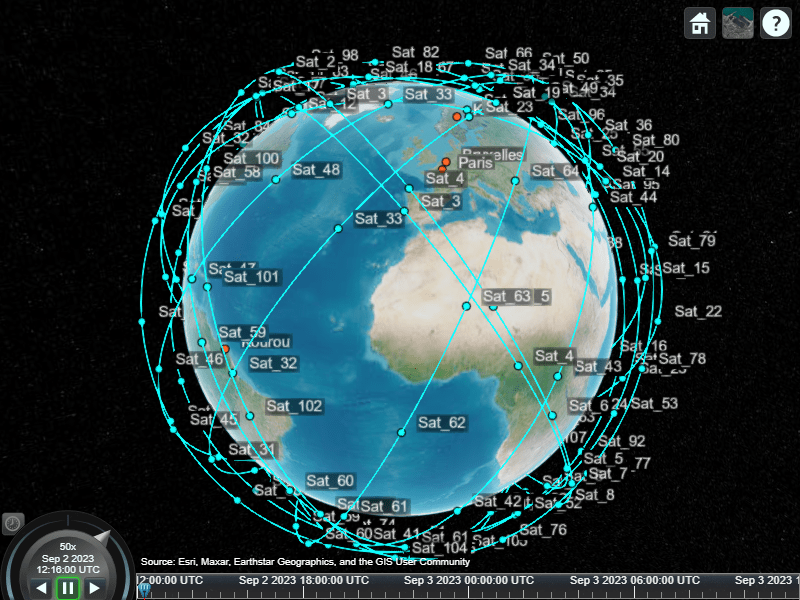
補助関数

このコードは関数 alt2radius を作成します。

function radiusMeters = alt2radius(altitude)
% Convert altitude in Mm to radius in m.

% Add the radius of the Earth in Mm.
radius = altitude + 6.378137; 

% Convert the radius to meters.
radiusMeters = radius * 1000 * 1000;
end

このコードは関数 observability を作成します。

function targetVisibilityPct = observability(numPlanes,satPerPlane,mission,...
                altitude,inclination,phasing,argLat)
% The radius is in megameters (1000s of km) to keep the optimization search
% bounded in [0.5 1.5], which is roughly low Earth orbit.

% Convert the radius to meters for walkerDelta setup.
radiusMeters = alt2radius(altitude);

mission.Constellation = walkerDelta(...
    mission.Scenario,...
    radiusMeters,...
    inclination,...
    satPerPlane*numPlanes,...
    numPlanes,...
    phasing,...
    ArgumentOfLatitude=argLat,...
    Name="Sat");

% Compute the access for each target.
targetVisibilityPct = zeros(numel(mission.Targets),1);
for targetIdx = 1:numel(mission.Targets)
    accessAnalysis = access(mission.Constellation,mission.Targets(targetIdx));
    satAccess = accessStatus(accessAnalysis);
    systemAccess = any(satAccess,1);
    targetVisibilityPct(targetIdx) = mean(systemAccess); 
end
end

参考

surrogateopt

トピック

• サロゲート最適化