このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。

遺伝的アルゴリズムの仕組み

アルゴリズムの概要

遺伝的アルゴリズムの仕組みを以下にまとめます。

1. アルゴリズムはランダムな初期集団を作成することから始まります。

2. 次に、アルゴリズムは一連の新しい集団を作成します。各ステップで、アルゴリズムは現在の世代の個体を使用して次の集団を作成します。新しい集団を作成するために、アルゴリズムは次の手順を実行します。

   1. 現在の集団の各メンバーの適応度値を計算してスコアを付けます。これらの値は生のフィットネススコアと呼ばれます。

   2. 生のフィットネス スコアをスケーリングして、より使いやすい値の範囲に変換します。これらのスケールされた値は期待値と呼ばれます。

   3. 期待に基づいて、親と呼ばれるメンバーを選択します。

   4. 現在の集団の中で適応度が低い個体の一部が エリート として選択されます。これらのエリート個体は次の集団に引き継がれます。

   5. 親から子供を産みます。子は、単一の親にランダムな変更を加えることによって（突然変異）、または一対の親のベクトルエントリを組み合わせることによって（交差）生成されます。

   6. 現在の人口を子供たちに置き換えて、次の世代を形成します。

3. 停止基準の 1 つが満たされると、アルゴリズムは停止します。アルゴリズムの停止条件を参照してください。

4. アルゴリズムは線形制約と整数制約に対して修正された手順を実行します。整数と線形制約を参照してください。

5. アルゴリズムは非線形制約に合わせてさらに変更されます。遺伝的アルゴリズムのための非線形制約ソルバーアルゴリズムを参照してください。

初期人口

アルゴリズムは、次の図に示すように、ランダムな初期集団を作成することから始まります。

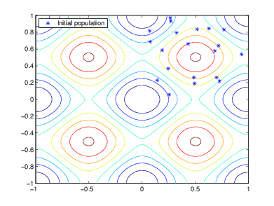
この例では、初期集団には 20 個の個体が含まれています。初期集団のすべての個体は図の右上象限に位置し、つまり座標は 0 から 1 の間にあることに注意してください。この例では、InitialPopulationRange オプションは [0;1] です。

関数の最小点がおおよそどこにあるかわかっている場合は、その点がその範囲の中央付近になるように InitialPopulationRange を設定する必要があります。たとえば、Rastrigin 関数の最小点が点 [0 0] の近くにあると考えられる場合、InitialPopulationRange を [-1;1] に設定できます。ただし、この例が示すように、遺伝的アルゴリズムは、InitialPopulationRange の選択が最適ではない場合でも最小値を見つけることができます。

次世代の創造

各ステップで、遺伝的アルゴリズムは現在の集団を使用して、次の世代を構成する子供を作成します。アルゴリズムは、現在の集団内の 親 と呼ばれる個体のグループを選択します。親は、自分の 遺伝子 (ベクトルのエントリ) を子供に提供します。アルゴリズムは通常、より優れた適応度値を持つ個体を親として選択します。SelectionFcn オプションで、アルゴリズムが親を選択するために使用する関数を指定できます。選択オプションを参照してください。

遺伝的アルゴリズムは、次の世代のために 3 種類の子を作成します。

• エリート 子供は、現在の世代で最も優れた適応度値を持つ個体です。これらの個体は自動的に次の世代まで生き残ります。

• 交差 子は、一対の親のベクトルを組み合わせることによって作成されます。

• 突然変異 子は、単一の親にランダムな変更、つまり突然変異を導入することによって作成されます。

次の図は、3 種類の子供を示しています。

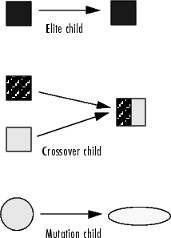
突然変異と交叉 は、アルゴリズムが生成する各タイプの子の数と、交差と突然変異を実行するために使用する関数を指定する方法について説明します。

次のセクションでは、アルゴリズムが交差と突然変異の子を作成する方法について説明します。

クロスオーバーチルドレン

アルゴリズムは、現在の集団内の親のペアを組み合わせることで交差子を作成します。子ベクトルの各座標では、デフォルトの交差関数が 2 つの親のいずれかから同じ座標にあるエントリ、つまり 遺伝子 をランダムに選択し、それを子に割り当てます。線形制約のある問題の場合、デフォルトのクロスオーバー関数は、親のランダムな加重平均として子を作成します。

突然変異の子供たち

このアルゴリズムは、個々の親の遺伝子をランダムに変更することで突然変異の子供を作成します。デフォルトでは、制約のない問題の場合、アルゴリズムはガウス分布からのランダムなベクトルを親に追加します。境界付きまたは線形制約付きの問題の場合、子は実行可能なままです。

次の図は、初期集団の子供、つまり第 2 世代の集団を示しており、それらがエリート、交差、または突然変異の子供であるかどうかを示しています。

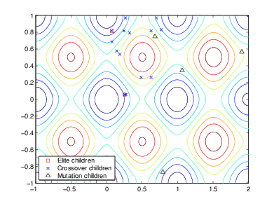
後世の陰謀

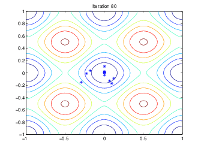
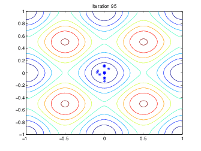
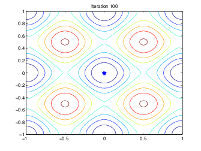
次の図は、反復 60、80、95、および 100 における集団を示しています。

世代数が増えるにつれて、集団内の個体は互いに近づき、最小点 [0 0] に近づきます。

アルゴリズムの停止条件

遺伝的アルゴリズムは、次のオプションを使用して停止するタイミングを決定します。opts = optimoptions('ga') を実行して各オプションのデフォルト値を確認してください。

• MaxGenerations — 世代数が MaxGenerations に達するとアルゴリズムは停止します。

• MaxTime — アルゴリズムは、 MaxTime に等しい秒数だけ実行された後に停止します。

• FitnessLimit — 現在の集団内の最良の点の適応度関数の値が FitnessLimit 以下になると、アルゴリズムは停止します。

• MaxStallGenerations — MaxStallGenerations にわたる適合度関数値の平均相対変化が Function tolerance 未満になると、アルゴリズムは停止します。

• MaxStallTime — MaxStallTime に等しい秒数の間に目的関数に改善が見られない場合、アルゴリズムは停止します。

• FunctionTolerance — アルゴリズムは、MaxStallGenerations にわたる適合度関数値の平均相対変化が Function tolerance 未満になるまで実行されます。

• ConstraintTolerance — ConstraintTolerance は停止基準として使用されません。非線形制約に関する実現可能性を判断するために使用されます。また、max(sqrt(eps),ConstraintTolerance) は線形制約に関して実現可能性を決定します。

これらの条件のいずれかが満たされるとすぐにアルゴリズムは停止します。

選択

選択関数は、適応度スケーリング関数からのスケーリングされた値に基づいて、次世代の親を選択します。スケーリングされた適応度値は期待値と呼ばれます。個体は親として複数回選択される可能性があり、その場合、その個体の遺伝子は複数の子に提供されます。デフォルトの選択オプション @selectionstochunif は、各親がそのスケール値に比例した長さの線の部分に対応する線をレイアウトします。アルゴリズムは、同じサイズのステップで線に沿って移動します。各ステップで、アルゴリズムは到達したセクションから親を割り当てます。

より決定論的な選択オプションは @selectionremainder であり、これは次の 2 つのステップを実行します。

• 最初のステップでは、関数は各個体のスケール値の整数部分に従って決定論的に親を選択します。たとえば、個体のスケール値が 2.3 の場合、関数はその個体を親として 2 回選択します。

• 2 番目のステップでは、選択関数は、確率的均一選択と同様に、スケールされた値の小数部分を使用して追加の親を選択します。この関数は、個々のスケール値の小数部に比例する長さのセクションに線を配置し、線に沿って等間隔で移動して親を選択します。

  Top スケーリングを使用する場合のように、スケーリングされた値の小数部分がすべて 0 に等しい場合、選択は完全に決定論的であることに注意してください。

詳細とその他の選択オプションについては、選択オプション を参照してください。

複製オプション

再生オプションは、遺伝的アルゴリズムが次世代を作成する方法を制御します。次のオプションがあります。

• EliteCount — 現在の世代で最高の適応度を持ち、次の世代まで生き残ることが保証されている個体の数。これらの人々はエリートの子供たちと呼ばれます。

  EliteCount が 1 以上の場合、最適な適応度値は世代ごとに減少するだけです。遺伝的アルゴリズムは適応度関数を最小化するため、これが望ましい結果となります。EliteCount を高い値に設定すると、最も適応した個体が集団を支配することになり、検索の効果が低下する可能性があります。

• CrossoverFraction — 交叉によって生成される、エリートの子供以外の次世代の個体の割合。変異と交差の変化 のトピック「交差率の設定」では、CrossoverFraction の値が遺伝的アルゴリズムのパフォーマンスにどのように影響するかについて説明します。

エリート個体はすでに評価されているため、ga は繁殖中にエリート個体の適応度関数を再評価しません。この動作は、個体の適応度関数がランダムではなく、決定論的な関数であると想定しています。この動作を変更するには、出力関数を使用します。EvalElitesのを参照してください。

突然変異と交叉

遺伝的アルゴリズムは、現在の世代の個体を使用して、次の世代を構成する子供を作成します。アルゴリズムは、現在の世代で最も適応度の高い個体に対応するエリートの子の他に、

• 現在の世代の個体のペアからベクトルエントリ、つまり遺伝子を選択して交叉し、それらを組み合わせて子を形成します。

• 現在の世代の単一の個体にランダムな変更を適用して子供を作成することにより、突然変異の子供を作成します。

どちらのプロセスも遺伝的アルゴリズムに不可欠です。クロスオーバーにより、アルゴリズムはさまざまな個体から最良の遺伝子を抽出し、それらを再結合して、潜在的に優れた子供を生み出すことができます。突然変異により集団の多様性が増し、アルゴリズムがより良い適応度を持つ個体を生成する可能性が高まります。

遺伝的アルゴリズムが突然変異と交差を適用する方法の例については、次世代の創造 を参照してください。

次のように、アルゴリズムが作成する各タイプの子の数を指定できます。

• EliteCount はエリートの子供の数を指定します。

• CrossoverFraction は、エリートの子供以外の、クロスオーバーの子供である人口の割合を指定します。

たとえば、PopulationSize が 20、EliteCount が 2、CrossoverFraction が 0.8 の場合、次の世代の各タイプの子の数は次のようになります。

• エリートの子供が二人います。

• エリートの子以外の個体は 18 個あるため、アルゴリズムは 0.8 * 18 = 14.4 を 14 に丸めて交差子の数を取得します。

• エリートの子供以外の残りの4人は突然変異の子供です。

整数と線形制約

問題に整数または線形制約 (境界を含む) がある場合、アルゴリズムは集団の進化を変更します。

• 問題に整数制約と線形制約の両方がある場合、ソフトウェアは生成されたすべての個体をそれらの制約に関して実行可能になるように変更します。任意の作成、突然変異、または交差関数を使用でき、集団全体が整数制約と線形制約に関して実行可能なままになります。

• 問題に線形制約のみがある場合、ソフトウェアはそれらの制約に関して実行可能になるように個体を変更しません。線形制約に関して実現可能性を維持する作成、突然変異、および交差関数を使用する必要があります。そうしないと、人口が実現不可能になり、結果が実現不可能になる可能性があります。デフォルトの演算子は線形実行可能性を維持します: 作成の場合は gacreationlinearfeasible または gacreationnonlinearfeasible、突然変異の場合は mutationadaptfeasible、交差の場合は crossoverintermediate。

整数および線形実行可能性の内部アルゴリズムは、surrogateopt のアルゴリズムと似ています。問題に整数制約と線形制約がある場合、アルゴリズムはまず線形に実行可能な点を作成します。次に、アルゴリズムは、点を線形に実行可能な状態に保つヒューリスティックを使用して、線形に実行可能な点を整数に丸めることで、整数制約を満たそうとします。このプロセスで集団を構築するのに十分な実行可能なポイントを取得できなかった場合、アルゴリズムは intlinprog を呼び出して、境界、線形制約、および整数制約に関して実行可能なポイントをさらに見つけようとします。

その後、突然変異または交差によって新しい集団メンバーが作成されるときに、アルゴリズムは同様の手順を実行して、新しいメンバーが整数かつ線形実行可能であることを確認します。各新しいメンバーは、必要に応じて、整数および線形の制約と境界を満たしながら、元の値に可能な限り近くなるように変更されます。

関連するトピック

• 遺伝的アルゴリズムの用語
• 遺伝的アルゴリズムのための非線形制約ソルバーアルゴリズム