Main Content

ハードウェア効率に優れたアルゴリズムを使用した複素数値線形方程式系の求解

スクリプトを開く

この例では、シストリック アレイを使用して、Simulink® のハードウェア効率に優れた MATLAB® コードを使用して複素数値線形方程式系を解く方法について説明します。この例で使用しているモデルでは、次の連立方程式を解くためのハードウェア効率に優れた方法を説明します。

$$AX = B$$

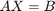
ここで、A は m 行 n 列の複素数行列で、X は n 行 p 列の複素数行列で、B は m 行 p 列の複素数行列です。

モデルを開く

fi_complex_mldivide_systolic_array_model モデルを開きます。

model = 'fi_complex_mldivide_systolic_array_model';
open_system(model)

データを送信する Enabled Subsystem には、次に送信する入力を把握する MATLAB Function ブロックが含まれており、ready 信号が High のとき、行列 A および B の行をブロック "4x4 Complex CORDIC Matrix Left Divide" に送信します。ready が High の状態でデータを送信した場合、パイプライン内に既に存在するデータが無効になることはありません。

アルゴリズムは行列 A を上三角行列 R で上書きします。アルゴリズムは B を C = Q'B で上書きします。ここで Q はユニタリで、QR = A です。アルゴリズムは、上三角行列方程式に後退代入を使用します。

$$RX = C.$$

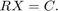
アルゴリズムを調査するため、ブロック "4x4 Complex CORDIC Matrix Left Divide" のマスク内を表示します。

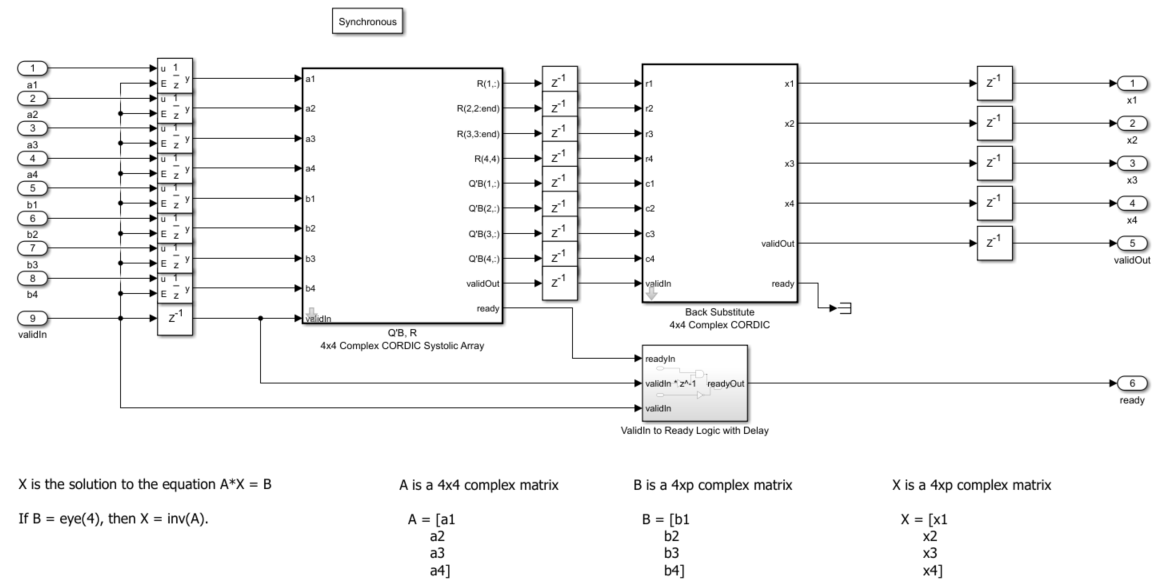
パラメーターの定義

ベース ワークスペースで複素数行列 A および B を定義します。この例では、行列 A は 4 行 4 列、行列 B は 4 行 p 列 (p は右辺の数) でなければなりません。

rng('default');
A = complex(randn(4,4),randn(4,4));
B = complex(randn(4,1),randn(4,1));

この手法では CORDIC アルゴリズムを使用するため、NumberOfCORDICIterations パラメーター、または "4x4 Complex CORDIC Matrix Left Divide" ブロックのブロック パラメーターに、CORDIC カーネルの反復回数も指定しなければなりません。

A と B が倍精度浮動小数点データ型の場合、CORDIC の反復回数には double の仮数のビット数を指定します。入力が固定小数点の場合、CORDIC 反復数は語長より小さくなければなりません。計算の精度は反復ごとに 1 ビットずつ、入力の語長まで向上します。このモデルは固定小数点データ型、double データ型、single データ型で動作します。

NumberOfCORDICIterations = 52;

また、後退代入で使用されるデータ型を指定するため、変数 BackSubstitutePrototype をインスタンス化するか、"4x4 Complex CORDIC Matrix Left Divide" ブロックのブロック パラメーターにプロトタイプ値を入力しなければなりません。この場合は、行列 A と B が double のため、BackSubstitutePrototype 値を double に設定します。この変数は、関数castにより、'like' 構文を使用して後退代入変数をキャストするために使用されます。

BackSubstitutePrototype = 0;

モデルのシミュレーション

予期される警告をオフにし、モデルをシミュレートします。

warning_state = warning('off','Coder:builtins:ConstantFoldingOverFlow');
sim(model)

シミュレーション後、モデルは行列 X に戻り、これが行列方程式の解になります。

$$AX = B$$

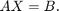
AX-B が小さい値であることをチェックし、結果を検証します。

err = norm(A*X - B)

err =

   6.5534e-15

QR アルゴリズム

CORDIC を使用した QR 分解の実行およびシストリック アレイでの CORDIC を使用したハードウェア効率に優れた QR 分解の実装の例のように、CORDIC アルゴリズムを使用して QR 分解が計算されます。

この例は 4 行 4 列の行列 A についてです。このモデル内にブロックを並べることで、任意のサイズの行列を作成できます。

QR アルゴリズムを確認するには、ブロック "Q'B, R 4x4 Complex CORDIC Systolic Array" のマスク内を表示します。

複素数の QR

この例のデータは複素数であるため、ピボットの虚数部をゼロにして実数値にするために追加のステップが必要になります。これは、データを実数部と虚数部に分け、CORDIC を使用して、実数行列の 2 つの行であるかのように虚数部をゼロにすることによって行います。これは、以下の複素数の乗算と等価です。

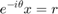
$$e^{-i\theta} x = r$$

ここで、

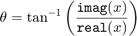
$$
\theta = \tan^{-1}\left({\mbox{\texttt{imag}}(x)\over \mbox{\texttt{real}}(x)}\right)
$$

および

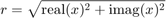
$$ r = \sqrt{\mbox{real}(x)^2 + \mbox{imag}(x)^2}$$

ただし、演算は CORDIC アルゴリズムを使用して、二乗や平方根を使用せずに行われます。

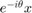$e^{-i\theta} x$ のアルゴリズムを確認するには、ブロック "Rotate first element to real" のマスク内を表示します。

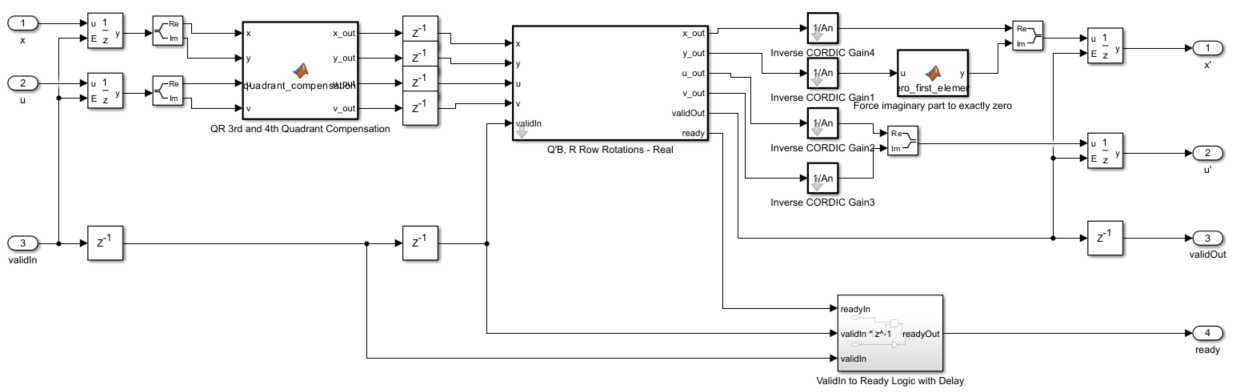
後退代入

最後に、X を計算するため、R の対角要素の逆数を計算し、右辺 C に後退代入します。アルゴリズムでは、CORDIC 除算実装を使用して逆数を計算します。

後退代入アルゴリズムを確認するには、ブロック "Back Substitute 4x4 Complex CORDIC" のマスク内を表示します。

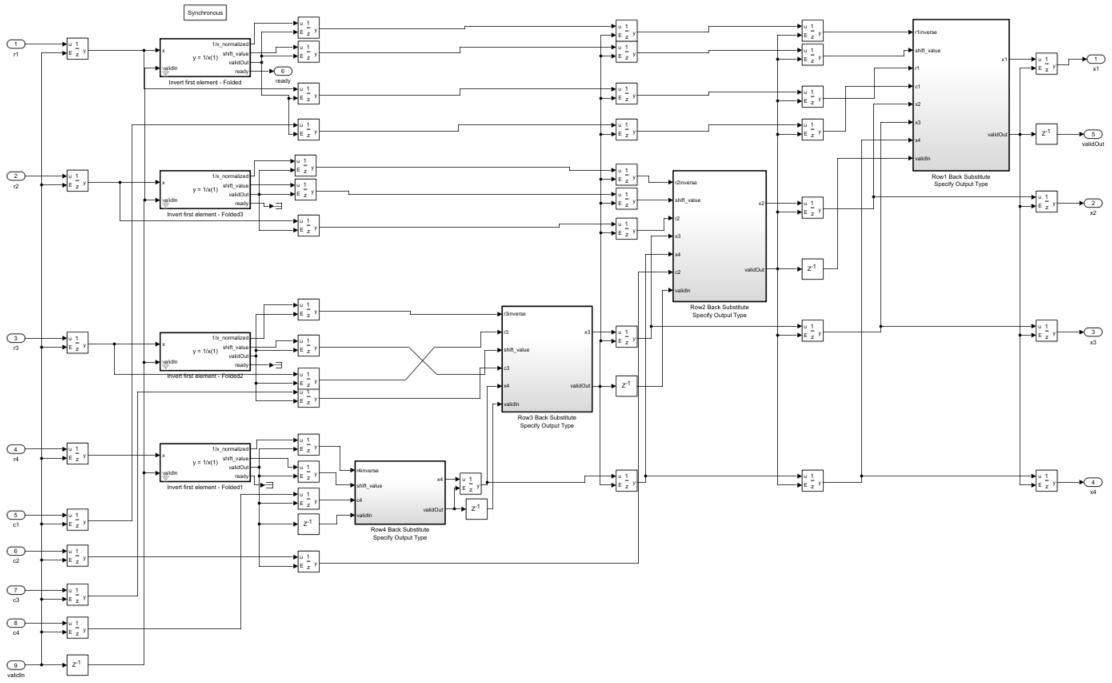
逆行列

通常、逆行列を明示的に計算することは必要ありません [3]、[5]。しかし、計算する場合、B を単位行列 I と等しくなるよう設定します。すると、以下の方程式の解は、

$$AX = I$$

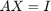
以下と等価になります。

$$X = A^{-1}.$$

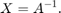
A = complex(2*rand(4,4)-1,2*rand(4,4)-1);
B = complex(eye(4));
NumberOfCORDICIterations = 52;
BackSubstitutePrototype = 0;

モデルのシミュレーションを実行します。

sim(model)

AX と XA が単位行列に近いことを確認します。丸め誤差により多少の差は生じます。

A*X

ans =

   1.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   1.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 + 0.0000i
  -0.0000 + 0.0000i   0.0000 - 0.0000i   1.0000 + 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   1.0000 - 0.0000i


X*A

ans =

   1.0000 - 0.0000i  -0.0000 - 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i
   0.0000 + 0.0000i   1.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.0000 + 0.0000i   1.0000 - 0.0000i  -0.0000 + 0.0000i
   0.0000 - 0.0000i  -0.0000 + 0.0000i  -0.0000 + 0.0000i   1.0000 + 0.0000i

非整数のスケーリング

非整数のデータ型に正規化すると、固定小数点の演算が簡単になります。データが [-1, +1] の範囲に収まるように行列をスケーリングして、小数固定小数点型を使用できます。なぜなら、以下の行列方程式の解は

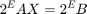
$$2^E AX = 2^EB$$

以下の式の解と同じだからです。

$$AX = B.$$

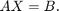
生成コードのコストを増やさずに非整数のスケーリングに変換するには、MATLAB の関数 reinterpretcast を使用するか、[等価な値をもつ入力と出力] を [整数格納 (SI)] に設定して Simulink の Data Type Conversion ブロックを使用します。

網羅的なテスト ポイントの実行

A および B の 3 次元配列を作成して、モデルから多くのテスト入力を実行できます。

m = 4;
n = 4;
p = 1;
n_test_inputs = 100;

実数部と虚数部が範囲 [-1, +1] に収まるように入力を作成します。

A = complex(2*rand(m,n,n_test_inputs)-1, 2*rand(m,n,n_test_inputs)-1);
B = complex(2*rand(m,p,n_test_inputs)-1, 2*rand(m,p,n_test_inputs)-1);

この例では、行列 A と B には既に [-1, +1] の範囲に収まる実数部と虚数部が含まれているため、型を非整数に設定します。

data_word_length = 24;
data_fraction_length = 23;

QR のデータ型

実数 QR 分解の R の要素の成長は 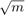$\sqrt{m}$ です (CORDIC を使用した QR 分解の実行を参照)。この例では要素は複素数であるため、追加の成長係数 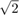$\sqrt{2}$ が必要です。その理由は以下であるからです。

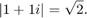
$$|1+1i| = \sqrt{2}.$$

また、CORDIC アルゴリズムは、以下のゲイン係数 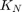$K_N$ を中間値まで拡大させます。ここで、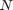$N$ は、正規化されるまでの CORDIC の反復回数です。

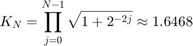
$$
K_N = \prod_{j=0}^{N-1}{\sqrt{1+2^{-2j}}} \approx 1.6468
$$

したがって、m 行 n 列の複素数行列 A の QR アルゴリズムの成長上限は、すべての成長係数の積です。

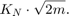
$$ K_N \cdot \sqrt{2m}.$$

この例では、A は 4 行 4 列のため、QR アルゴリズムの最大成長係数は以下のとおりです。

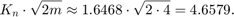
$$K_n \cdot \sqrt{2m} \approx 1.6468 \cdot \sqrt{2\cdot 4} = 4.6579.$$

したがって、m=4 行のとき、オーバーフローを防ぐために QR アルゴリズムで許可する追加の整数ビットの数は、次のようになります。

qr_growth_bits = ceil(log2(1.6468*sqrt(2*m)))

qr_growth_bits =

     3

行列 A および B の固定小数点へのキャスト

モデルでは、入力が符号付きで、B の語長が A の語長と同じであることが必要です。

QR の成長に対応できるよう、データの語長を増やします。

qr_input_word_length = data_word_length + qr_growth_bits

qr_input_word_length =

    27

A を固定小数点にキャストし、B を A の型にキャストします。

T.A = fi([], 1, qr_input_word_length, data_fraction_length);
T.B = T.A;

A = cast(A,'like',T.A);
B = cast(B,'like',T.B);

後退代入のデータ型

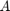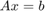$A$ が $n$ 行 $n$ 列の可逆複素数行列で、$x$ が行列方程式 $Ax=b$ の解である場合、ベクトルと行列のノルムのプロパティを使用することで (例は参考文献 [6] を参照)、以下が示されます。

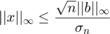
$$
||x||_\infty \leq \frac{\sqrt{n}||b||_\infty}{\sigma_n}
$$

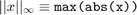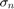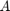ここで、$||x||_\infty \equiv \mbox{\texttt{max(abs(x))}}$ と $\sigma_n$ は、$A$ の最も小さい特異値です。この境界は、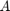$A$ の条件数に関連しています。

この例では、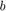$b$ は、1 を境界値とする、実数部と虚数部をもつ複素数ベクトルです。そのため、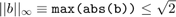$||b||_\infty \equiv \mbox{\texttt{max(abs(b))}}\leq \sqrt{2}$ となります。

したがって、この問題の 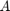$A$ 行列の特異値の分布が既知の場合、与えられた確率で、後退代入でのオーバーフローを避けるために必要な追加の整数ビット数を選択できます (例は参考文献 [1] を参照)。

この例では、テスト ベンチ内のすべての行列について特異値を計算し、それに基づいて、オーバーフローを避ける整数ビット数を選択します。

singular_values = zeros(n,n_test_inputs);
A0 = double(A);
for k = 1:n_test_inputs
    singular_values(:,k) = svd(A0(:,:,k));
end
condition_numbers = singular_values(1,:)./singular_values(end,:);
x_bound = sqrt(2*n)./singular_values(end,:);

追加する増加分ビット数は、最大値の範囲の底を 2 とする対数です。

integer_bits_for_backsubstitute = ceil(log2(max(x_bound)))

integer_bits_for_backsubstitute =

     7

語長から後退代入に必要な整数ビットと符号ビット用の追加ビットを減算します。

backsubstitute_fraction_length = T.A.WordLength - integer_bits_for_backsubstitute - 1

backsubstitute_fraction_length =

    19

そのため、後退代入のデータ型は次のようになります。

BackSubstitutePrototype = fi(0, 1, T.A.WordLength, backsubstitute_fraction_length)

BackSubstitutePrototype = 

     0

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 27
        FractionLength: 19

CORDIC の反復回数を、A の固定小数点語長より 1 少ない数に設定します。

NumberOfCORDICIterations = T.A.WordLength - 1

NumberOfCORDICIterations =

    26

固定小数点の入力を使用してモデルをシミュレートします。

sim(model)

誤差の計算とプロット

誤差の測定値は以下のようになります。

norm(AX - B)

これは、入力 A と B の各ペアについてです。

norm_error = zeros(1,size(X,3));
B0 = double(B);
X0 = double(X);
for k = 1:size(X,3)
    norm_error(k) = norm(A0(:,:,k)*X0(:,:,k) - B0(:,:,k));
end

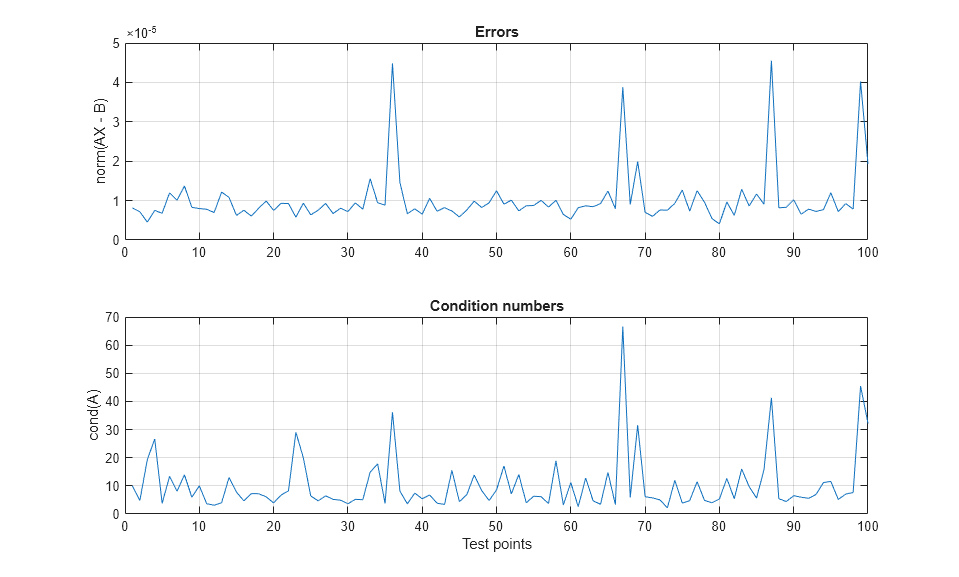
誤差をプロットします。選択されたデータ型により、誤差は小さくなっています。理論から予測されるとおり、通常、行列 A の条件数が大きいとき、誤差は大きくなります。

figure(1)
clf
h1 = subplot(2,1,1);
plot(norm_error)
grid on
title('Errors')
ylabel('norm(AX - B)')
h2 = subplot(2,1,2);
plot(condition_numbers)
grid on
title('Condition numbers')
ylabel('cond(A)')
xlabel('Test points')
linkaxes([h1,h2],'x')

警告を再度有効にします。

warning(warning_state);

参考文献

[1] Zizhong Chen and Jack J. Dongarra."Condition Numbers of Gaussian Random Matrices".SIAM Journal on Matrix Analysis and Applications.27.3 (July 2005), pp. 603-620.

[2] George E. Forsythe and Cleve B. Moler.Computer Solution of Linear Algebraic Systems.Englewood Cliffs, N.J.:Prentice-Hall, 1967.

[3] George E. Forsythe, M.A. Malcom and Cleve B. Moler.Computer Methods for Mathematical Computations.Englewood Cliffs, N.J.:Prentice-Hall, 1977.

[4] Cleve B. Moler.Cleve's Corner:What is the Condition Number of a Matrix?>, The MathWorks, Inc. 2017.

[5] Cleve B. Moler.Numerical Computing with MATLAB.SIAM, 2004. isbn:978-0-898716-60-3.

[6] Gene H. Golub and Charles F. Van Loan.Matrix Computations.The Johns Hopkins University Press.

%#ok<*NOPTS,*NASGU>

関連するトピック