シストリックアレイでの CORDIC を使用したハードウェア効率に優れた QR 分解の実装

この例では、Simulink® でハードウェア効率に優れた MATLAB® コードを使用して行列の QR 分解を計算する方法を示します。

方程式系を解く、つまり QR 分解を使用して行列方程式 AX = B の最小二乗解を計算するには、R と Q'B を計算します。ここで QR = A および RX = Q'B です。R は上三角行列、Q は直交行列です。Q と R だけが必要な場合は、B を単位行列に設定します。

この例では、CORDIC アルゴリズムを使用してギブンス回転を適用して、行列 A から R が計算されています。C = Q'B は、同じギブンス回転を適用して行列 B から計算されています。このアルゴリズムでは反復的なシフトと加算のみを使用してこれらの計算を実行します。

この例で使用されるアルゴリズムの詳細については、CORDIC を使用した QR 分解の実行を参照してください。

概要

この例で使用される Simulink モデルは次のとおりです。

fxpdemo_real_4x4_systolic_array_QR_model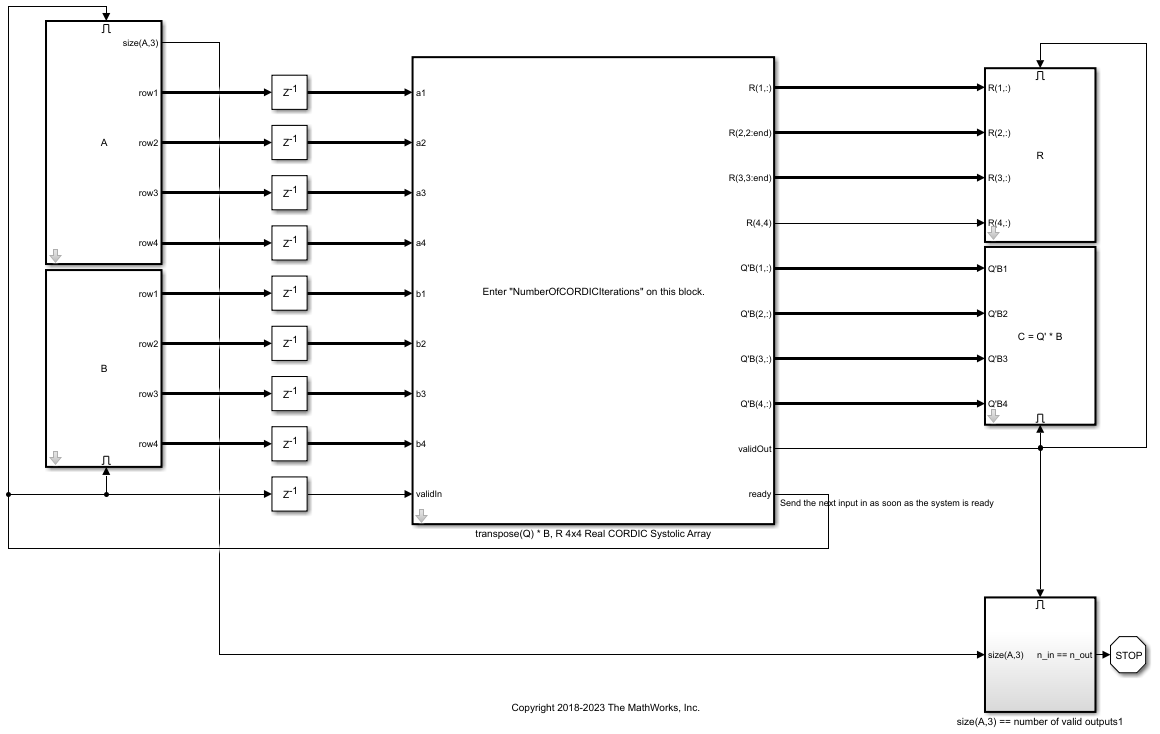

独自の入力行列 A と B を入力するには、対応する有効なサブシステムブロックのブロックパラメーターを左側に開きます。シミュレーション後、モデルは計算された出力行列 C = Q'B および R をワークスペースに返しますtranspose(Q)*B, R 4x4 Real CORDIC Systolic Array サブシステムのブロックパラメーターで CORDIC 反復数を指定します。入力が固定小数点の場合、CORDIC 反復数は語長より小さくなければなりません。計算の精度は反復ごとに 1 ビットずつ、入力の語長まで向上します。

このモデルは固定小数点データ型、double データ型、single データ型で動作します。

アルゴリズムでの因数分解の実行方法を確認するには、transpose(Q)*B, R 4x4 Real CORDIC Systolic Array サブシステムのマスク内を確認します。注釈には、下対角要素をゼロ設定するために演算されている行列の行が示されます。シストリックアレイは 4 行 4 列の行列 A に対して設定されますが、同じパターンに従ってどのサイズにも拡張できます。この実装は、実数入力行列でのみ動作します。

CORDIC を使用してギブンス回転を実行する MATLAB Function ブロックの MATLAB コードを確認するには、引き続きブロックマスク内を確認します。

この例では、A の行数と列数が 4 でなければなりません。行列 B には 4 つの行がなければなりませんが、列数は任意です。

QR を使用して行列方程式 Ax = B を解く

行列方程式 AX = B を解く最初のステップは RX = Q'B を計算することです。ここで、R は上三角、Q は直交で Q*R = A です。

以下の入力は倍精度浮動小数点型であるため、反復数は double の仮数のビット数である 52 に設定します。

format
NumberOfCORDICIterations = 52;
A = 2*rand(4,4)-1;
B = 2*rand(4,4)-1;

モデルをシミュレーションして R および C = Q'B を計算します。

sim fxpdemo_real_4x4_systolic_array_QR_model
R
C

R =

    1.5149   -0.0519    1.7292   -0.3224
         0    0.9593   -0.0259   -0.0879
         0         0    0.2565    1.0888
         0         0         0   -0.6429


C =

    0.5942   -0.2382    0.0676   -0.9370
   -0.8887    0.6146   -0.5758    0.3051
    0.1725    0.7339    0.5409    0.5374
    0.8540    1.1078   -0.2183   -0.5620

R および C = Q'B で後退代入すると MATLAB と同じ結果になることを確認します。

X = R\C
X_should_be = A\B

X =

   -7.1245  -12.1131   -0.6637    1.4236
   -0.8779    0.7572   -0.5511    0.3545
    6.3113   10.1759    0.6673   -1.6155
   -1.3283   -1.7231    0.3396    0.8741


X_should_be =

   -7.1245  -12.1131   -0.6637    1.4236
   -0.8779    0.7572   -0.5511    0.3545
    6.3113   10.1759    0.6673   -1.6155
   -1.3283   -1.7231    0.3396    0.8741

組み込みの MATLAB の解と CORDIC QR の解の差のノルムは小さくなります。

norm(X - X_should_be)

ans =

   3.2578e-14

Q および R の計算

Q および R を計算するには、B を単位行列と等価に設定します。B が単位行列と等しい場合、Q = C' になります。

NumberOfCORDICIterations = 52;
A = 2*rand(4,4)-1;
B = eye(size(A,1),'like',A);
sim fxpdemo_real_4x4_systolic_array_QR_model

Q = C';

理論的な QR 分解は QR==A であるため、計算された QR と A の差は小さくなります。

norm(Q*R - A)

ans =

   2.2861e-15

QR は一意ではない

QR 分解が一意であるのは R の行と Q の列の符号までです。R の対角要素をすべて正にすると、一意の QR 分解にすることができます。

D = diag(sign(diag(R)));
Qunique = Q*D
Runique = D*R

Qunique =

   -0.3086    0.1224   -0.1033   -0.9376
   -0.6277   -0.7636   -0.0952    0.1174
   -0.5573    0.3930    0.7146    0.1559
    0.4474   -0.4975    0.6852   -0.2877


Runique =

    1.4459   -0.8090    0.1547    0.3977
         0    1.1441    0.0809   -0.2494
         0         0    0.8193    0.1894
         0         0         0    0.4836

次に、モデルから計算された QR と MATLAB の組み込み関数 QR を比較できます。

[Q0,R0] = qr(A);
D0 = diag(sign(diag(R0)));
Q0 = Q0*D0
R0 = D0*R0

Q0 =

   -0.3086    0.1224   -0.1033   -0.9376
   -0.6277   -0.7636   -0.0952    0.1174
   -0.5573    0.3930    0.7146    0.1559
    0.4474   -0.4975    0.6852   -0.2877


R0 =

    1.4459   -0.8090    0.1547    0.3977
         0    1.1441    0.0809   -0.2494
         0         0    0.8193    0.1894
         0         0         0    0.4836

ハードウェア効率の高い実装のための固定小数点の使用

固定小数点入力データ型を使用して、ASIC や FPGA デバイス向けの効率的な HDL コードを生成します。

オーバーフローしない固定小数点データ型の選択方法の詳細については、CORDIC を使用した QR 分解の実行の例を参照してください。

A および B の 3 次元配列を作成して、モデルから多くのテスト入力を実行できます。

n_test_inputs=100;

次のセクションでは、-1 ～ 1 でスケーリングされる行列 A と B の乱数入力を定義するために、固定小数点の語長を 18 ビット、小数部の長さを 14 ビットに設定して QR 分解の成長と CORDIC アルゴリズムの中間計算を可能にします。

word_length = 18;
fraction_length = 14;

CORDIC 反復の最高精度数は語長から 1 を引いた数です。CORDIC 反復数が word_length - 1 より小さい値に設定されると、次の Ready 信号への遅延と時間刻みが短くなりますが、精度は低くなります。生成されたコードは固定小数点の語長よりも大きいシフトをサポートしていないため、CORDIC 反復数はこれより大きい値に設定できません。

NumberOfCORDICIterations = word_length - 1

NumberOfCORDICIterations =

    17

乱数テスト入力は連結されて、時間 k における入力は A(:,:,k) および B(:,:,k) になります。A および B の各要素は、-1 ～ +1 の一様な確率変数になります。

A = 2*rand(4,4,n_test_inputs)-1;

Q=C' となるように単位行列として B を選択します。

B = eye(4);
B = repmat(B,1,1,n_test_inputs);

A を固定小数点にキャストし、B を A と同様にキャストします。

A = fi(A,1,word_length,fraction_length);
B = cast(B,'like',A);

モデルのシミュレーションを実行します。

sim fxpdemo_real_4x4_systolic_array_QR_model

誤差の計算とプロット

norm_error = zeros(1,size(R,3));
for k = 1:size(R,3)
    Q_times_R_minus_A = double(C(:,:,k))'*double(R(:,:,k)) - double(A(:,:,k));
    norm_error(k) = norm(Q_times_R_minus_A);
end

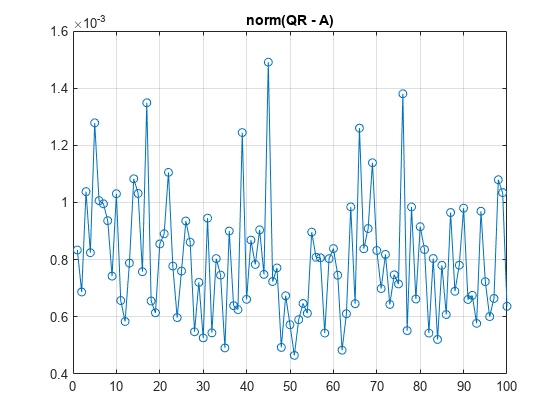
誤差は 10^-3 と同程度になります。

clf
plot(norm_error,'o-')
grid on
title('norm(QR - A)')

%#ok<*NASGU,*NOPTS>

シストリック アレイでの CORDIC を使用したハードウェア効率に優れた QR 分解の実装

概要