関数 fiaccel を使用した派生範囲に基づくデータ型の推奨
この例では、関数 fiaccel を使用して静的範囲に基づいて固定小数点データ型を推奨する方法を示します。派生範囲に基づいてデータ型を推奨すると、動作範囲全体にわたってアルゴリズムを実行するテスト ファイルを提供する必要がないというメリットがあります。このようなテスト ファイルは実行に非常に長い時間がかかることが多いため、代わりに派生範囲を使用すると時間を節約できます。
メモ
派生範囲の解析は非スカラー変数ではサポートされていません。
前提条件
この例を実行するには、次の製品をインストールしなければなりません。
MATLAB®
Fixed-Point Designer™
C コンパイラ
サポートされるコンパイラ を参照してください。
mex -setupを使用して既定のコンパイラを変更できます。既定のコンパイラの変更を参照してください。
新規フォルダーの作成と関連ファイルのコピー
ローカルの書き込み可能なフォルダーに、関数
dti.mを作成します。関数
dtiは MATLAB の Discrete Time Integrator を実装します。function [y, clip_status] = dti(u_in) %#codegen % Discrete Time Integrator in MATLAB % % Forward Euler method, also known as Forward % Rectangular, or left-hand approximation. % The resulting expression for the output of % the block at step 'n' is % y(n) = y(n-1) + K * u(n-1) % init_val = 1; gain_val = 1; limit_upper = 500; limit_lower = -500; % Variable to hold state between % consecutive calls to this block persistent u_state; if isempty(u_state) u_state = init_val+1; end % Compute Output if (u_state > limit_upper) y = limit_upper; clip_status = -2; elseif (u_state >= limit_upper) y = limit_upper; clip_status = -1; elseif (u_state < limit_lower) y = limit_lower; clip_status = 2; elseif (u_state <= limit_lower) y = limit_lower; clip_status = 1; else y = u_state; clip_status = 0; end % Update State tprod = gain_val * u_in; u_state = y + tprod;
テスト ファイル
dti_test.mを作成してdtiアルゴリズムの演習を行います。このテスト スクリプトは正弦波入力を使用して関数
dtiを実行します。その後、スクリプトは入力および出力信号をプロットします。% dti_test % cleanup clear dti % input signal x_in = sin(2.*pi.*(0:0.001:2)).'; pause(10); len = length(x_in); y_out = zeros(1,len); is_clipped_out = zeros(1,len); for ii=1:len data = x_in(ii); % call to the dti function init_val = 0; gain_val = 1; upper_limit = 500; lower_limit = -500; % call to the design that does DTI [y_out(ii), is_clipped_out(ii)] = dti(data); end figure('Name', [mfilename, '_plot']); subplot(2,1,1) plot(1:len,x_in) xlabel('Time') ylabel('Amplitude') title('Input Signal (Sin)') subplot(2,1,2) plot(1:len,y_out) xlabel('Time') ylabel('Amplitude') title('Output Signal (DTI)') disp('Test complete.');
次のような事前処理と事後処理を行う別のテスト スクリプトを作成することをお勧めします。
入力の読み込み
入力値の設定
テスト結果の出力
| タイプ | 名前 | 説明 |
|---|---|---|
| 関数のコード | dti.m | エントリポイントの MATLAB 関数 |
| テスト ファイル | dti_test.m | MATLAB スクリプト。次をテストします。 dti.m |
固定小数点の構成オブジェクトのセットアップ
固定小数点の構成オブジェクトを作成し、テスト ファイル名を設定します。
fixptcfg = coder.config('fixpt'); fixptcfg.TestBenchName = 'dti_test';
設計範囲の指定
関数 dti の入力パラメーター u_in の設計範囲情報を指定します。
fixptcfg.addDesignRangeSpecification('dti', 'u_in', -1.0, 1.0)
シミュレーション データ インスペクターによるプロット作成の有効化
テスト ファイルを実行することを選択し、生成された固定小数点の MATLAB コードを検証します。比較プロット用に入力データと出力データを記録し、その結果をシミュレーション データ インスペクターでプロットするようにします。
fixptcfg.TestNumerics = true; fixptcfg.LogIOForComparisonPlotting = true; fixptcfg.PlotWithSimulationDataInspector = true;
範囲の派生と固定小数点コードの生成
関数 fiaccel を使用して、浮動小数点の MATLAB 関数 dti を固定小数点の MATLAB コードに変換します。固定小数点のデータ型の既定の語長を 16 に設定します。
fixptcfg.ComputeDerivedRanges = true; fixptcfg.ComputeSimulationRanges = false; fixptcfg.DefaultWordLength = 16; % Derive ranges and generate fixed-point code fiaccel -float2fixed fixptcfg dti
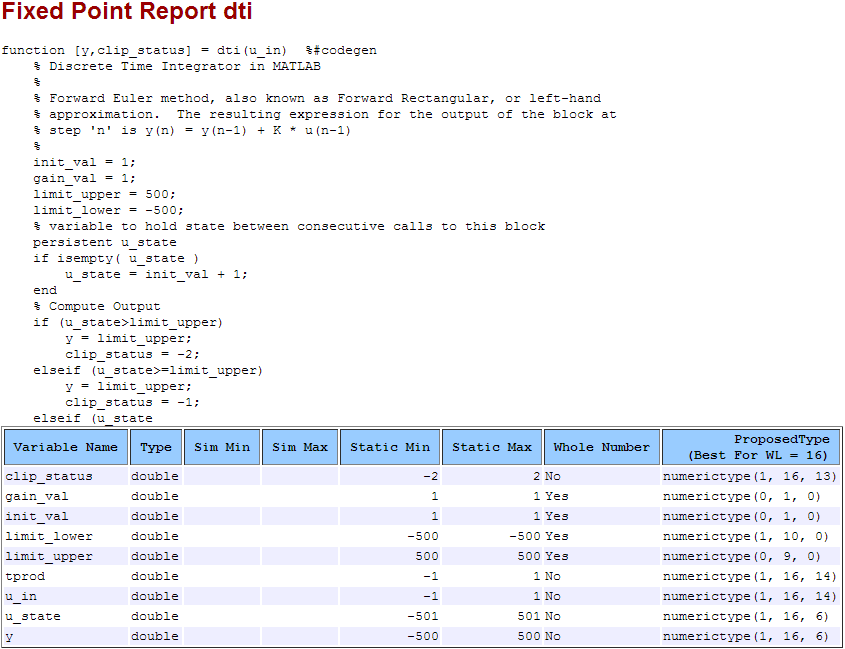
fiaccel によって浮動小数点のコードが解析されます。関数 dti の入力型を指定しなかったため、変換プロセスではテスト ファイルのシミュレーションによって型が推定されます。次に変換プロセスによってアルゴリズム内の変数の範囲を派生します。これらの派生範囲を使用して変数の固定小数点型が推奨されます。変換が完了すると、型推奨レポートが生成されます。
派生範囲情報の表示
関数 dti の型推奨レポート dti_report.html へのリンクをクリックします。
レポートが Web ブラウザーで開きます。
生成された固定小数点の MATLAB コードの表示
fiaccel によって関数 dti の固定小数点バージョン dti_fxpt.m および dti_fxpt を呼び出すラッパー関数が生成されます。これらのファイルはローカルの作業フォルダーの codegen\dti\fixpt フォルダーに生成されます。
function [y, clip_status] = dti_fixpt(u_in) %#codegen
% Discrete Time Integrator in MATLAB
%
% Forward Euler method, also known as
% Forward Rectangular, or left-hand approximation.
% The resulting expression for the output of the
% block at step 'n' is y(n) = y(n-1) + K * u(n-1)
%
fm = get_fimath();
init_val = fi(1,0,1,0,fm);
gain_val = fi(1,0,1,0,fm);
limit_upper = fi(500,0,9,0,fm);
limit_lower = fi(-500,1,10,0,fm);
% variable to hold state between
% consecutive calls to this block
persistent u_state;
if isempty(u_state)
u_state = fi(init_val+fi(1,0,1,0,fm),1,16,6,fm);
end
% Compute Output
if (u_state > limit_upper)
y = fi(limit_upper, 1, 16, 6, fm);
clip_status = fi(-2, 1, 16, 13, fm);
elseif (u_state >= limit_upper)
y = fi(limit_upper, 1, 16, 6, fm);
clip_status = fi(-1, 1, 16, 13, fm);
elseif (u_state < limit_lower)
y = fi(limit_lower, 1, 16, 6, fm);
clip_status = fi(2, 1, 16, 13, fm);
elseif (u_state <= limit_lower)
y = fi(limit_lower, 1, 16, 6, fm);
clip_status = fi(1, 1, 16, 13, fm);
else
y = fi(u_state, 1, 16, 6, fm);
clip_status = fi(0, 1, 16, 13, fm);
end
% Update State
tprod = fi(gain_val * u_in, 1, 16, 14, fm);
u_state(:) = y + tprod;
end
function fm = get_fimath()
fm = fimath('RoundingMethod','Floor',...
'OverflowAction','Wrap',...
'ProductMode','FullPrecision',...
'MaxProductWordLength',128,...
'SumMode','FullPrecision',...
'MaxSumWordLength',128);
end
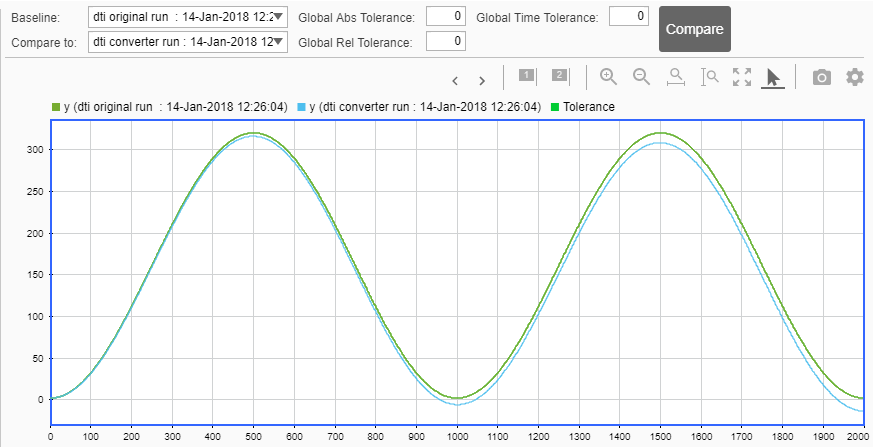
浮動小数点の実行と固定小数点の実行の比較
比較プロット用の入力と出力の記録と、プロットにシミュレーション データ インスペクターを使用することを選択したため、シミュレーション データ インスペクターが開きます。
シミュレーション データ インスペクターを使用して、浮動小数点と固定小数点の実行情報の表示や結果の比較を行うことができます。たとえば [比較] タブで出力 y の浮動小数点の値と固定小数点の値を比較するには、[y] を選択して [実行の比較] をクリックします。
シミュレーション データ インスペクターは、ベースラインの浮動小数点の実行と固定小数点の実行のプロットおよびそれらの差を表示します。