量子化誤差の計算
この例では、さまざまな丸め手法を使用する場合に、信号の量子化誤差の統計値を計算および比較する方法を説明します。量子化は、データ型で値を正確に表現できない場合に発生します。このような場合、その値はデータ型で表現できる最も近い値に丸める必要があります。
まず、quantizer オブジェクトの範囲内にランダム信号が作成されます。次に、'fix'、'floor'、'ceil'、'nearest'、'convergent' といった丸め手法で信号が量子化されて、信号の統計値が推測されます。
量子化誤差の論理的確率密度関数は、関数 errpdf を使用して計算されます。量子化誤差の理論的平均値は、関数 errmean を使用して計算されます。また、量子化誤差の理論的分散は、関数 errvar で計算されます。
一様分布ランダム信号の作成
固定小数点 quantizer オブジェクト q の -1 ~ 1 の領域に及ぶ一様分布ランダム信号を作成します。
q = quantizer([8 7]); r = realmax(q); u = r*(2*rand(50000,1) - 1); xi = linspace(-2*eps(q),2*eps(q),256);
Fix: ゼロ方向への丸め
'fix' 丸めでは、確率密度関数は、他と比べて幅が 2 倍となります。このため、分散は他の 4 倍となります。
q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
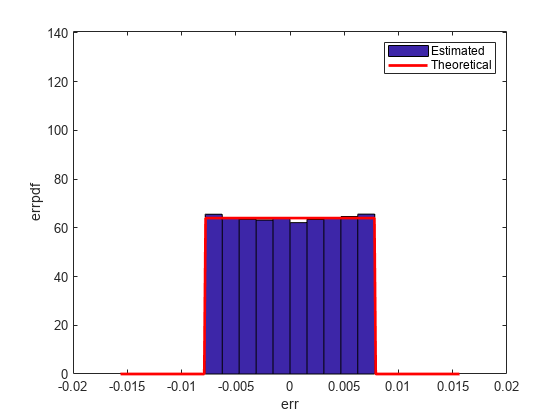
理論的分散は eps(q)^2/3 で、理論的平均値は 0 です。
Floor: 負の無限大方向への丸め
'floor' 丸めは、2 の補数表現を使用して表される固定小数点数や整数と共に使用される場合は切り捨てと呼ばれます。実装にハードウェアが必要ないため、DSP プロセッサの丸めモードでは最も一般的です。'floor' は、'round' ほどには実際値に近い量子化された値を生成しませんが、同じ分散になります。'floor' を使用すると、符号が異なる小さな信号が検出されます。'round' ではそれらは失われます。
q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062

理論的分散は eps(q)^2/12 で、理論的平均値は -eps(q)/2 です。
Ceil: 正の無限大方向への丸め
q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062

理論的分散は eps(q)^2/12 で、理論的平均値は eps(q)/2 です。
Round: 最も近い整数への丸め。等距離では、最も大きい方向への丸め
'round' は 'floor' より正確ですが、eps(q) より小さい値はすべてゼロに丸められ、失われます。
q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0

理論的分散は eps(q)^2/12 で、理論的平均値は 0 です。
Convergent: 最も近い整数への丸め。等距離では、偶数方向への丸め
'convergent' 丸めは、等距離を常に同じ方向へ丸める通常の 'round' によって生じるバイアスを除去します。
q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0

理論的分散は eps(q)^2/12 で、理論的平均値は 0 です。
最も近い整数方向への丸めと最も近い偶数方向への丸めの比較
プロットを見ただけでは、偶数丸め誤差と最も近い正の整数方向への丸めの確率密度関数を区別するのは困難です。
最も近い偶数方向への丸め誤差の確率密度関数は、
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
最も近い整数方向への丸め誤差の確率密度関数は、
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
最も近い整数方向への丸めは正の方向へわずかにバイアスがありますが、最も近い偶数方向への丸め誤差の確率密度関数は対称的です。
唯一の違いは、等距離における丸めの方向です。
x = (-3.5:3.5)'; [x convergent(x) nearest(x)]
ans = 8×3
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000