filter

Filter disturbances using univariate ARIMA or ARIMAX model

Syntax

Y = filter(Mdl,Z)

[Y,E,V] = filter(Mdl,Z)

Tbl2 = filter(Mdl,Tbl1)

[___] = filter(___,Name,Value)

Description

Y = filter(Mdl,Z) returns the numeric array of one or more response series Y resulting from filtering the numeric array of one or more underlying disturbance series Z through the fully specified, univariate ARIMA model Mdl. Z is associated with the model innovations process that drives the specified ARIMA model.

[Y,E,V] = filter(Mdl,Z) also returns numeric arrays of model innovations E and, when Mdl represents a composite conditional mean and variance model, conditional variances V, resulting from filtering the disturbance paths Z through the model Mdl.

Tbl2 = filter(Mdl,Tbl1) returns the table or timetable Tbl2 containing the results from filtering the paths of disturbances in the input table or timetable Tbl1 through Mdl. The disturbance variable in Tbl1 is associated with the model innovations process through Mdl. (since R2023b)

filter selects the variable Mdl.SeriesName, or the sole variable in Tbl1, as the disturbance variable to filter through the model. To select a different variable in Tbl1 to filter through the model, use the DisturbanceVariable name-value argument.

[___] = filter(___,Name,Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. filter returns the output argument combination for the corresponding input arguments. For example, filter(Mdl,Z,Z0=PS,X=Pred) filters the numeric vector of disturbances Z through the ARIMAX Mdl, and specifies the numeric vector of presample disturbance data PS to initialize the model and the exogenous predictor data X for the regression component.

Examples

Filter Vector of Disturbances Through Model

Compute the impulse response function (IRF) of an ARMA model by filtering a vector of zeros, representing disturbances, through the model.

Specify a mean zero ARMA(2,0,1) model.

Mdl = arima(Constant=0,AR={0.5 -0.8},MA=-0.5, ...
    Variance=0.1);

Simulate the first 20 responses of the IRF. Generate a disturbance series with a one-time, unit impulse, and then filter it.

z = [1; zeros(19,1)];
y = filter(Mdl,z);

y is a 20-by-1 response path resulting from filtering the disturbance path z through the model. y represents the IRF. The filter function requires one presample observation to initialize the model. By default, filter uses the unconditional mean of the process, which is 0.

y = y/y(1);

Normalize the IRF such that the first element is 1.

Plot the impulse response function.

figure
stem((0:numel(y)-1)',y,"filled");
title("Impulse Response")

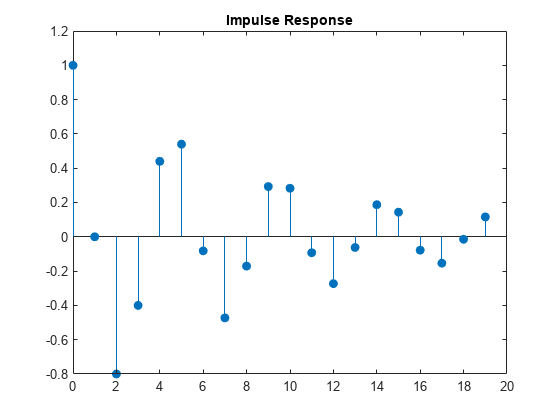
The impulse response assesses the dynamic behavior of a system to a one-time, unit impulse.

Alternatively, you can use the impulse function to plot the IRF for an ARIMA process.

Simulate and Filter Multiple Paths

Filter a matrix of disturbance paths. Return the paths of responses and innovations, which drive the data-generating processes.

Create a mean zero ARIMA(2,0,1) model.

Mdl = arima(Constant=0,AR={0.5,-0.8},MA=-0.5, ...
    Variance=0.1);

Generate 20 random, length 100 paths from the model.

rng(1,"twister"); % For reproducibility
[ySim,eSim,vSim] = simulate(Mdl,100,NumPaths=20);

ySim, eSim, and vSim are 100-by-20 matrices of 20 simulated response, innovation, and conditional variance paths of length 100, respectively. Because Mdl does not have a conditional variance model, vSim is a matrix completely composed of the value of Mdl.Variance.

Obtain disturbance paths by standardizing the simulated innovations.

zSim = eSim./sqrt(vSim);

Filter the disturbance paths through the model.

[yFil,eFil] = filter(Mdl,zSim);

yFil and eFil are 100-by-20 matrices. The columns are independent paths generated from filtering corresponding disturbance paths in zSim through the model Mdl.

Confirm that the outputs of simulate and filter are identical.

sameE = norm(eSim - eFil) < eps

sameE = logical
   1

sameY = norm(ySim - yFil) < eps

sameY = logical
   1

The logical values 1 confirm the outputs are effectively identical.

Filter Disturbance Path in Timetable

Since R2023b

Fit an ARIMA(1,1,1) model to the weekly average NYSE closing prices. Supply a timetable of data and specify the series for the fit. Then, filter randomly generated Gaussian noise paths through the estimated model to simulate responses and innovations.

Load Data

Load the US equity index data set Data_EquityIdx.

load Data_EquityIdx
T = height(DataTimeTable)

T = 
3028

The timetable DataTimeTable includes the time series variable NYSE, which contains daily NYSE composite closing prices from January 1990 through December 2001.

Plot the daily NYSE price series.

figure
plot(DataTimeTable.Time,DataTimeTable.NYSE)
title("NYSE Daily Closing Prices: 1990 - 2001")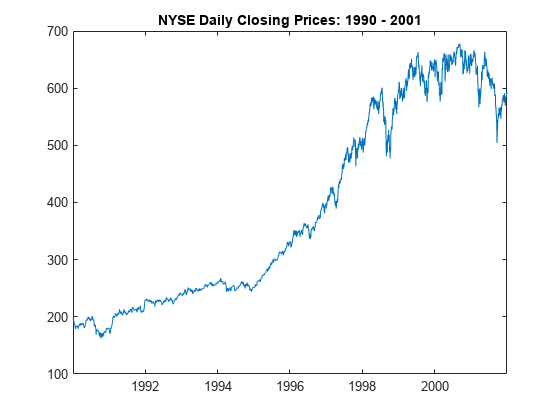

Prepare Timetable for Estimation

When you plan to supply a timetable, you must ensure it has all the following characteristics:

• The selected response variable is numeric and does not contain any missing values.

• The timestamps in the Time variable are regular, and they are ascending or descending.

Remove all missing values from the timetable, relative to the NYSE price series.

DTT = rmmissing(DataTimeTable,DataVariables="NYSE");
T_DTT = height(DTT)

T_DTT = 
3028

Because all sample times have observed NYSE prices, rmmissing does not remove any observations.

Determine whether the sampling timestamps have a regular frequency and are sorted.

areTimestampsRegular = isregular(DTT,"days")

areTimestampsRegular = logical
   0

areTimestampsSorted = issorted(DTT.Time)

areTimestampsSorted = logical
   1

areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Business day rules make daily macroeconomic measurements irregular.

Remedy the time irregularity by computing the weekly average closing price series of all timetable variables.

DTTW = convert2weekly(DTT,Aggregation="mean");
areTimestampsRegular = isregular(DTTW,"weeks")

areTimestampsRegular = logical
   1

T_DTTW = height(DTTW)

T_DTTW = 
627

DTTW is regular.

figure
plot(DTTW.Time,DTTW.NYSE)
title("NYSE Daily Closing Prices: 1990 - 2001")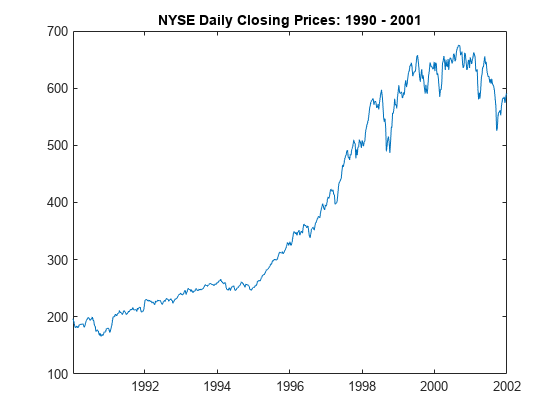

Create Model Template for Estimation

Suppose that an ARIMA(1,1,1) model is appropriate to model NYSE composite series during the sample period.

Create an ARIMA(1,1,1) model template for estimation. Set the response series name to NYSE.

Mdl = arima(1,1,1);
Mdl.SeriesName = "NYSE";

Mdl is a partially specified arima model object.

Fit Model to Data

Fit an ARIMA(1,1,1) model to weekly average NYSE closing prices. Specify the entire series.

EstMdl = estimate(Mdl,DTTW);

 
    ARIMA(1,1,1) Model (Gaussian Distribution):
 
                 Value      StandardError    TStatistic      PValue   
                ________    _____________    __________    ___________

    Constant     0.86385       0.46496         1.8579          0.06318
    AR{1}       -0.37582       0.22719        -1.6542         0.098093
    MA{1}        0.47221       0.21741         2.1719          0.02986
    Variance       55.89         1.832         30.507      2.1204e-204

EstMdl is a fully specified, estimated arima model object. By default, estimate backcasts for the required Mdl.P = 2 presample responses.

Filter Random Gaussian Disturbance Paths

Generate 2 random, independent series of length T_DTTW from the standard Gaussian distribution. Store the matrix of series as one variable in DTTW.

rng(1,"twister") % For reproducibility
DTTW.Z = randn(T_DTTW,2);

DTTW contains a new variable called Z containing a T_DTTW-by-2 matrix of two disturbance paths.

Filter the paths of disturbances through the estimated ARIMA model. Specify the table variable name containing the disturbance paths.

Tbl2 = filter(EstMdl,DTTW,DisturbanceVariable="Z");
tail(Tbl2)

       Time         NYSE     NASDAQ              Z               NYSE_Response        NYSE_Innovation      NYSE_Variance 
    ___________    ______    ______    _____________________    ________________    ___________________    ______________

    16-Nov-2001    577.11    1886.9     -1.8948      0.41292    358.78    433.57    -14.166       3.087    55.89    55.89
    23-Nov-2001       583    1898.3      1.3583      0.27051    367.95    436.63     10.155      2.0223    55.89    55.89
    30-Nov-2001    581.41    1925.8     -0.9118       1.1119    363.35    445.61    -6.8165      8.3125    55.89    55.89
    07-Dec-2001    584.96    1998.1    -0.14964       -2.418    361.61    428.95    -1.1187     -18.077    55.89    55.89
    14-Dec-2001    574.03      1981    -0.40114      0.98498     359.6     434.9    -2.9989      7.3636    55.89    55.89
    21-Dec-2001     582.1    1967.9    -0.57758    0.0039243    355.48    437.04     -4.318    0.029338    55.89    55.89
    28-Dec-2001    590.28    1967.2      2.0039     -0.92415    370.84     430.2     14.981     -6.9089    55.89    55.89
    04-Jan-2002     589.8    1950.4    -0.50964     -0.43856    369.19    427.09    -3.8101     -3.2787    55.89    55.89

size(Tbl2)

ans = 1×2

   627     6

Tbl2 is a 627-by-6 timetable containing all variables in DTTW, and the two filtered response paths NYSE_Response, innovation paths NYSE_Innovation, and constant variance paths NYSE_Variance (Mdl.Variance = 55.89).

Supply Presample Responses

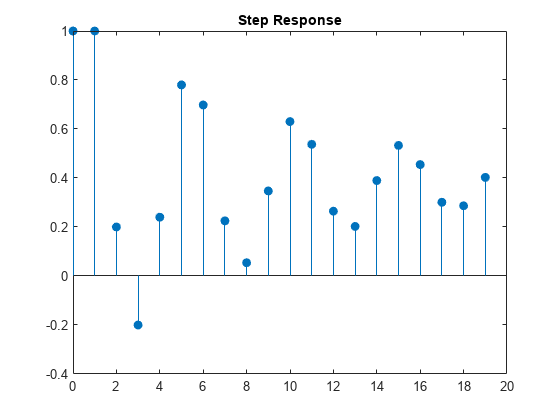
Assess the dynamic behavior of a system to a persistent change in a variable by plotting a step response. Supply presample responses to initialize the model.

Specify a mean zero ARIMA(2,0,1) process.

Mdl = arima(Constant=0,AR={0.5 -0.8},MA=-0.5, ...
    Variance=0.1);

Simulate the first 20 responses to a sequence of unit disturbances. Generate a disturbance series of ones, and then filter it. Set all presample observations equal to zero.

Z = ones(20,1);
Y = filter(Mdl,Z,Y0=zeros(Mdl.P,1));
Y = Y/Y(1);

The last step normalizes the step response function to ensure that the first element is 1.

Plot the step response function.

figure
stem((0:numel(Y)-1)',Y,"filled");
title("Step Response")

Simulate Responses from ARIMAX Model

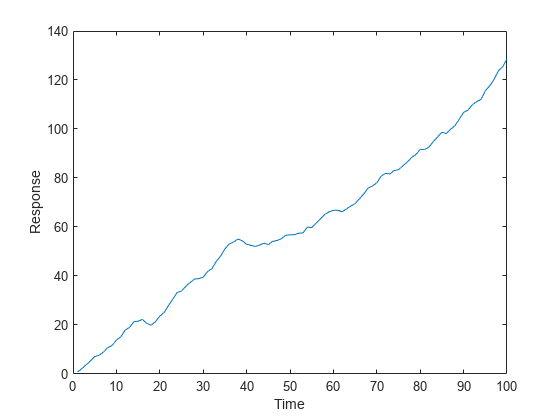
Create models for the response and predictor series. Set an ARIMAX(2,1,3) model to the response MdlY, and an AR(1) model to the MdlX.

MdlY = arima(AR={0.1 0.2},D=1,MA={-0.1 0.1 0.05}, ...
    Constant=1,Variance=0.5,Beta=2);
MdlX = arima(AR=0.5,Constant=0,Variance=0.1);

Simulate a length 100 predictor series x and a series of iid normal disturbances z having mean zero and variance 1.

rng(1,"twister")
z = randn(100,1);
x = simulate(MdlX,100);

Filter the disturbances z using MdlY to produce the response series y. Plot y.

y = filter(MdlY,z,X=x);
figure
plot(y);
xlabel("Time")
ylabel("Response")

Filter Disturbances Through Composite Conditional Mean and Variance Model

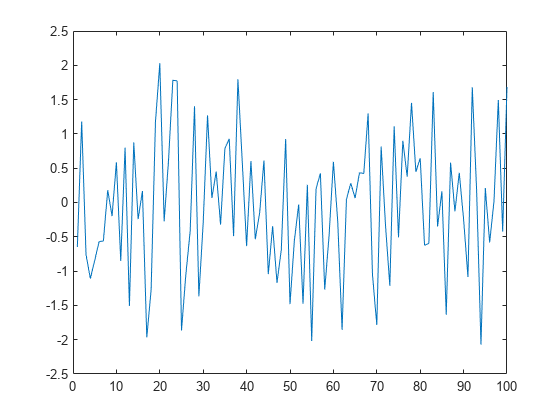
Create the composite AR(1)/GARCH(1,1) model

$$\begin{array}{l}{y}_t=1+0.5y_{t-1}+{\epsilon }_t\\ {\epsilon }_t={\sigma }_t{z}_t\\ {\sigma }_t^2=0.2+0.1{\sigma }_{t-1}^2+0.05{\epsilon }_{t-1}^2\\ z_t\sim N(0,1).\end{array}$$

Create the composite model.

CVMdl = garch(Constant=0.2,GARCH=0.1,ARCH=0.05);
Mdl = arima(Constant=1,AR=0.5,Variance=CVMdl)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,0,0) Model (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 1
               D: 0
               Q: 0
        Constant: 1
              AR: {0.5} at lag [1]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: [GARCH(1,1) Model]

Mdl is an arima object. The property Mdl.Variance contains a garch object that represents the conditional variance model.

Generate a random series of 100 standard Gaussian of disturbances.

rng(1,"twister") % For reproducibility
z = randn(100,1);

Filter the disturbances through the model. Return and plot the simulated conditional variances.

[y,e,v] = filter(Mdl,z);
plot(z)

Input Arguments

Mdl — Fully specified ARIMA model

arima model object

Fully specified ARIMA model, specified as an arima model object created by arima or estimate.

The properties of Mdl cannot contain NaN values.

Z — Disturbance series paths z_t

numeric column vector | numeric matrix

Underlying disturbance paths z_t, specified as a numobs-by-1 numeric column vector or numobs-by-numpaths numeric matrix. numObs is the length of the time series (sample size). numpaths is the number of separate, independent disturbance paths.

z_t drives the innovation process ε_t. For a variance process σ_t², the innovation process is

$${\epsilon }_t={\sigma }_t{z}_t.$$

Each row corresponds to a sampling time. The last row contains the latest set of disturbances.

Each column corresponds to a separate, independent path of disturbances. filter assumes that disturbances across any row occur simultaneously.

Z is the continuation of the presample disturbances Z0.

Data Types: double

Tbl1 — Time series data

table | timetable

Since R2023b

Time series data containing the observed disturbance variable z_t, associated with the model innovations process ε_t, and, optionally, predictor variables x_t, specified as a table or timetable with numvars variables and numobs rows. You can optionally select the disturbance variable or numpreds predictor variables by using the DisturbanceVariable or PredictorVariables name-value arguments, respectively.

For a variance process σ_t², the innovation process is

$${\epsilon }_t={\sigma }_t{z}_t.$$

Each row is an observation, and measurements in each row occur simultaneously. The selected disturbance variable is a single path (numobs-by-1 vector) or multiple paths (numobs-by-numpaths matrix) of numobs observations of disturbance data.

Each path (column) of the selected disturbance variable is independent of the other paths, but path j of all presample and in-sample variables correspond, for j = 1,…,numpaths. Each selected predictor variable is a numobs-by-1 numeric vector representing one path. The filter function includes all predictor variables in the model when it filters each disturbance path. Variables in Tbl1 represent the continuation of corresponding variables in Presample.

If Tbl1 is a timetable, it must represent a sample with a regular datetime time step (see isregular), and the datetime vector Tbl1.Time must be strictly ascending or descending.

If Tbl1 is a table, the last row contains the latest observation.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: filter(Mdl,Z,Z0=PS,X=Pred) specifies the numeric vector of presample disturbance data PS to initialize the model and the exogenous predictor data X for the regression component.

DisturbanceVariable — Disturbance variable z_t to select from Tbl1

string scalar | character vector | integer | logical vector

Since R2023b

Disturbance variable z_t to select from Tbl1 containing the disturbance data to filter through Mdl, specified as one of the following data types:

• String scalar or character vector containing a variable name in Tbl1.Properties.VariableNames

• Variable index (positive integer) to select from Tbl1.Properties.VariableNames

• A logical vector, where DisturbanceVariable(j) = true selects variable j from Tbl1.Properties.VariableNames

The selected variable must be a numeric vector and cannot contain missing values (NaNs).

If Tbl1 has one variable, the default specifies that variable. Otherwise, the default matches the variable to names in Mdl.SeriesName.

Example: DisturbanceVariable="StockRateDist"

Example: DisturbanceVariable=[false false true false] or DisturbanceVariable=3 selects the third table variable as the disturbance variable.

Data Types: double | logical | char | cell | string

Y0 — Presample response data y_t

numeric column vector | numeric matrix

Presample response data y_t to initialize the model, specified as a numpreobs-by-1 numeric column vector or a numpreobs-by-numprepaths numeric matrix. Use Y0 only when you supply the numeric array of disturbance data Z.

numpreobs is the number of presample observations. numprepaths is the number of presample response paths.

Each row is a presample observation (sampling time), and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be at least Mdl.P to initialize the AR model component. If numpreobs > Mdl.P, filter uses the latest required observations only.

Columns of Y0 are separate, independent presample paths. The following conditions apply:

• If Y0 is a column vector, it represents a single response path. filter applies it to each output path.

• If Y0 is a matrix, each column represents a presample response path. filter applies Y0(:,j) to initialize path j. numprepaths must be at least numpaths. If numprepaths > numpaths, filter uses the first size(Z,2) columns only.

By default, filter sets any necessary presample responses to one of the following values:

• The unconditional mean of the model when Mdl represents a stationary AR process without a regression component

• Zero when Mdl represents a nonstationary process or when it contains a regression component

Data Types: double

Z0 — Presample disturbance data z_t

numeric column vector | numeric matrix

Presample disturbance data z_t providing initial values for the input disturbance series Z, specified as a numpreobs-by-1 numeric column vector or a numpreobs-by-numprepaths numeric matrix. Use Z0 only when you supply the numeric array of disturbance data Z.

Each row is a presample observation (sampling time), and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be at least Mdl.Q to initialize the MA model component. If Mdl.Variance is a conditional variance model (for example, a garch model object), filter can require more rows than Mdl.Q. If numpreobs is larger than required, filter uses the latest required observations only.

Columns of Z0 are separate, independent presample paths. The following conditions apply:

• If Z0 is a column vector, it represents a single disturbance path. filter applies it to each output path.

• If Z0 is a matrix, each column represents a presample disturbance path. filter applies Z0(:,j) to initialize path j. numprepaths must be at least numpaths. If numprepaths > numpaths, filter uses the first size(Z,2) columns only.

By default, filter sets the necessary presample disturbances to zero.

Data Types: double

V0 — Presample conditional variance data σ_t²

positive numeric column vector | positive numeric matrix

Presample conditional variance data σ_t² used to initialize the conditional variance model, specified as a numpreobs-by-1 positive numeric column vector or a numpreobs-by-numprepaths positive numeric matrix. If the conditional variance Mdl.Variance is constant, filter ignores V0. Use V0 only when you supply the numeric array of disturbance data Z.

Each row is a presample observation (sampling time), and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be at least Mdl.Q to initialize the conditional variance model in Mdl.Variance. For details, see the filter function of conditional variance models. If numpreobs is larger than required, filter uses the latest required observations only.

Columns of V0 are separate, independent presample paths. The following conditions apply:

• If V0 is a column vector, it represents a single path of conditional variances. filter applies it to each output path.

• If V0 is a matrix, each column represents a presample path of conditional variances. filter applies V0(:,j) to initialize path j. numprepaths must be at least numpaths. If numprepaths > numpaths, filter uses the first size(Z,2) columns only.

By default, filter sets all necessary presample conditional variances to the unconditional variance of the conditional variance process.

Data Types: double

Presample — Presample data

table | timetable

Since R2023b

Presample data containing paths of response y_t, disturbance z_t, or conditional variance σ_t² series to initialize the model, specified as a table or timetable, the same type as Tbl1, with numprevars variables and numpreobs rows. Use Presample only when you supply a table or timetable of data Tbl1.

Each selected variable is a single path (numpreobs-by-1 vector) or multiple paths (numpreobs-by-numprepaths matrix) of numpreobs observations representing the presample of the response, disturbance, or conditional variance series for DisturbanceVariable, the selected disturbance variable in Tbl1.

Each row is a presample observation, and measurements in each row occur simultaneously. numpreobs must be one of the following values:

• At least Mdl.P when Presample provides only presample responses

• At least Mdl.Q when Presample provides only presample disturbances or conditional variances

• At least max([Mdl.P Mdl.Q]) otherwise

When Mdl.Variance is a conditional variance model, filter can require more than the minimum required number of presample values.

If you supply more rows than necessary, filter uses the latest required number of observations only.

If Presample is a timetable, all the following conditions must be true:

• Presample must represent a sample with a regular datetime time step (see isregular).

• The inputs Tbl1 and Presample must be consistent in time such that Presample immediately precedes Tbl1 with respect to the sampling frequency and order.

• The datetime vector of sample timestamps Presample.Time must be ascending or descending.

If Presample is a table, the last row contains the latest presample observation.

By default, filter sets the following values:

• For necessary presample responses:

  • The unconditional mean of the model when Mdl represents a stationary AR process without a regression component

  • Zero when Mdl represents a nonstationary process or when it contains a regression component.

• For necessary presample disturbances, zero.

• For necessary presample conditional variances, the unconditional variance of the conditional variance model n Mdl.Variance.

If you specify the Presample, you must specify the presample response, disturbance, or conditional variance name by using the PresampleResponseVariable, PresampleDisturbanceVariable, or PresampleVarianceVariable name-value argument.

PresampleResponseVariable — Response variable y_t to select from Presample

string scalar | character vector | integer | logical vector

Since R2023b

Response variable y_t to select from Presample containing presample response data, specified as one of the following data types:

• String scalar or character vector containing a variable name in Presample.Properties.VariableNames

• Variable index (positive integer) to select from Presample.Properties.VariableNames

• A logical vector, where PresampleResponseVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric matrix and cannot contain missing values (NaNs).

If you specify presample response data by using the Presample name-value argument, you must specify PresampleResponseVariable.

Example: PresampleResponseVariable="Stock0"

Example: PresampleResponseVariable=[false false true false] or PresampleResponseVariable=3 selects the third table variable as the presample response variable.

Data Types: double | logical | char | cell | string

PresampleDisturbanceVariable — Disturbance variable z_t to select from Presample

string scalar | character vector | integer | logical vector

Since R2023b

Disturbance variable z_t to select from Presample containing presample disturbance data, specified as one of the following data types:

• String scalar or character vector containing a variable name in Presample.Properties.VariableNames

• Variable index (positive integer) to select from Presample.Properties.VariableNames

• A logical vector, where PresampleDisturbanceVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric matrix and cannot contain missing values (NaNs).

If you specify presample disturbance data by using the Presample name-value argument, you must specify PresampleDisturbanceVariable.

Example: PresampleDisturbanceVariable="StockRateDist0"

Example: PresampleDisturbanceVariable=[false false true false] or PresampleDisturbanceVariable=3 selects the third table variable as the presample disturbance variable.

Data Types: double | logical | char | cell | string

PresampleVarianceVariable — Conditional variance variable σ_t² to select from Presample

string scalar | character vector | integer | logical vector

Since R2023b

Conditional variance variable σ_t² to select from Presample containing presample conditional variance data, specified as one of the following data types:

• String scalar or character vector containing a variable name in Presample.Properties.VariableNames

• Variable index (positive integer) to select from Presample.Properties.VariableNames

• A logical vector, where PresampleVarianceVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric vector and cannot contain missing values (NaNs).

If you specify presample conditional variance data by using the Presample name-value argument, you must specify PresampleVarianceVariable.

Example: PresampleVarianceVariable="StockRateVar0"

Example: PresampleVarianceVariable=[false false true false] or PresampleVarianceVariable=3 selects the third table variable as the presample conditional variance variable.

Data Types: double | logical | char | cell | string

X — Exogenous predictor data

numeric matrix

Exogenous predictor data for the regression component in the model, specified as a numeric matrix with numpreds columns. numpreds is the number of predictor variables (numel(Mdl.Beta)). Use X only when you supply the numeric array of disturbance data Z.

X must have at least numobs rows. The last row contains the latest predictor data. If X has more than numobs rows, filter uses only the latest numobs rows. Each row of X corresponds to each period in Z (period for which filter filters errors; the period after the presample).

filter does not use the regression component in the presample period.

Columns of X are separate predictor variables.

filter applies X to each filtered path; that is, X represents one path of observed predictors.

By default, filter excludes the regression component, regardless of its presence in Mdl.

Data Types: double

PredictorVariables — Exogenous predictor variables x_t to select from Tbl1

string vector | cell vector of character vectors | vector of integers | logical vector

Since R2023b

Exogenous predictor variables x_t to select from Tbl1 containing predictor data for the regression component, specified as one of the following data types:

• String vector or cell vector of character vectors containing numpreds variable names in Tbl1.Properties.VariableNames

• A vector of unique indices (positive integers) of variables to select from Tbl1.Properties.VariableNames

• A logical vector, where PredictorVariables(j) = true selects variable j from Tbl1.Properties.VariableNames

The selected variables must be numeric vectors and cannot contain missing values (NaNs).

By default, filter excludes the regression component, regardless of its presence in Mdl.

Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]

Example: PredictorVariables=[true false true false] or PredictorVariable=[1 3] selects the first and third table variables to supply the predictor data.

Data Types: double | logical | char | cell | string

Note

• NaN values in Z, X, Y0, Z0, and V0 indicate missing values. filter removes missing values from specified data by list-wise deletion.

  • For the presample, filter horizontally concatenates the possibly jagged arrays Y0, Z0, and V0 with respect to the last rows, and then it removes any row of the concatenated matrix containing at least one NaN.

  • For in-sample data, filter horizontally concatenates the possibly jagged arrays Z and X, and then it removes any row of the concatenated matrix containing at least one NaN.

  This type of data reduction reduces the effective sample size and can create an irregular time series.

• For numeric data inputs, filter assumes that you synchronize the presample data such that the latest observations occur simultaneously.

• filter issues an error when any table or timetable input contains missing values.

Output Arguments

Y — Simulated response paths y_t

numeric column vector | numeric matrix

Simulated response paths y_t, returned as a length numobs column vector or a numobs-by-numpaths numeric matrix. filter returns Y only when you supply the input Z.

For each t = 1, …, numobs, the simulated response at time t Y(t,:) corresponds to the filtered disturbance at time t Z(t,:) and response path j Y(:,j) corresponds to the filtered disturbance path j Z(:,j).

Y represents the continuation of the presample response paths in Y0.

E — Simulated paths of model innovations ε_t

numeric column vector | numeric matrix

Simulated paths of model innovations ε_t, returned as a length numobs column vector or a numobs-by-numpaths numeric matrix. filter returns E only when you supply the input Z. The dimensions of Y and E correspond.

Columns of E are scaled disturbance paths (innovations) such that, for a particular path

$${\epsilon }_t={\sigma }_t{z}_t.$$

V — Conditional variance paths σ_t²

numeric column vector | numeric matrix

Conditional variance paths σ_t², returned as a length numobs column vector or numobs-by-numpaths numeric matrix. filter returns V only when you supply the input Z. The dimensions of Y and V correspond.

If Z is a matrix, then the columns of V are the filtered conditional variance paths corresponding to the columns of Z.

Columns of V are conditional variance paths of corresponding paths of innovations ε_t (E) such that, for a particular path

$${\epsilon }_t={\sigma }_t{z}_t.$$

V represents the continuation of the presample conditional variance paths in V0.

Tbl2 — Simulated response y_t, innovation ε_t, and conditional variance σ_t² paths

table | timetable

Since R2023b

Simulated response y_t, innovation ε_t, and conditional variance σ_t² paths, returned as a table or timetable, the same data type as Tbl1. filter returns Tbl2 only when you supply the input Tbl1.

Tbl2 contains the following variables:

• The simulated response paths, which are in a numobs-by-numpaths numeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the disturbance variable in Tbl1. filter names the simulated response variable in Tbl2 responseName_Response, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is StockReturns, Tbl2 contains a variable for the corresponding simulated response paths with the name StockReturns_Response.

• The simulated innovation paths, which are in a numobs-by-numpaths numeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the disturbance variable in Tbl1. filter names the simulated innovation variable in Tbl2 responseName_Innovation, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is StockReturns, Tbl2 contains a variable for the corresponding simulated innovation paths with the name StockReturns_Innovation.

• The simulated conditional variances paths, which are in a numobs-by-numpaths numeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the disturbance variable in Tbl1. filter names the simulated conditional variance variable in Tbl2 responseName_Variance, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is StockReturns, Tbl2 contains a variable for the corresponding simulated conditional variance paths with the name StockReturns_Variance.

• All variables Tbl1.

If Tbl1 is a timetable, row times of Tbl1 and Tbl2 are equal.

Alternative Functionality

filter generalizes simulate; both functions filter a series of disturbances to produce output responses, innovations, and conditional variances. However, simulate autogenerates a series of mean zero, unit variance, independent and identically distributed (iid) disturbances according to the distribution in Mdl. In contrast, filter enables you to directly specify custom disturbances.

References

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.

[2] Enders, Walter. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, Inc., 1995.

[3] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.

Version History

Introduced in R2012b

R2023b: filter accepts input data in tables and timetables, and returns results in tables and timetables

In addition to accepting input data (in-sample and presample) in numeric arrays, filter accepts input data in tables or regular timetables. When you supply data in a table or timetable, the following conditions apply:

• filter chooses the default in-sample disturbance series and predictor data on which to operate, but you can use the specified optional name-value argument to select a different series.

• If you specify optional presample data to initialize the model, you must also specify the presample response, disturbance, or conditional variance series name.

• filter returns results in a table or timetable.

Name-value arguments to support tabular workflows include:

• DisturbanceVariable specifies the name of the disturbance series to select from the input data to filter through the model.

• Presample specifies the input table or timetable of presample response, disturbance, and conditional variance data.

• PresampleResponseVariable specifies the name of the response series to select from Presample.

• PresampleDisturbanceVariable specifies the name of the disturbance series to select from Presample.

• PresampleVarianceVariable specifies the name of the conditional variance series to select from Presample.

• PredictorVariables specifies the names of the predictor series to select from the input data for a model regression component.