Farrow 構造を使用した非整数遅延フィルター
この例では、Farrow 構造を使用してデジタル非整数遅延フィルターを設計する方法を示します。デジタル非整数遅延フィルターは、信号のサンプリングの瞬間を微調整するのに便利なツールです。これらは通常、遅延パラメーターが時間とともに変化するデジタル モデムの同期に使用されます。この例では、Farrow 構造が時変 FIR 非整数遅延フィルターを実装するための一般的な方法である理由を示します。
理想非整数遅延フィルター
理想非整数遅延フィルターは、線形位相オールパス フィルターです。そのインパルス応答は、非因果フィルターに対応した時間シフト離散 sinc 関数です。インパルス応答は無限であるので、時間の有限シフトによって因果性をもたせることはできません。そのため、フィルターを実現することはできず、近似しなければなりません。
Farrow 構造
非整数遅延フィルターの出力を計算するには、既存の離散時間サンプル間の入力信号値を推定する必要があります。特殊な内挿フィルターを使用して、任意の点における新しいサンプル値を計算できます。内挿フィルターの中でも、多項式ベースのフィルターは、その特殊な構造、つまり Farrow 構造のおかげで係数を簡単に処理できるので、特に有用です。特に、Farrow 構造の調整可能性により、これは実用的なハードウェアの実装に適しています。
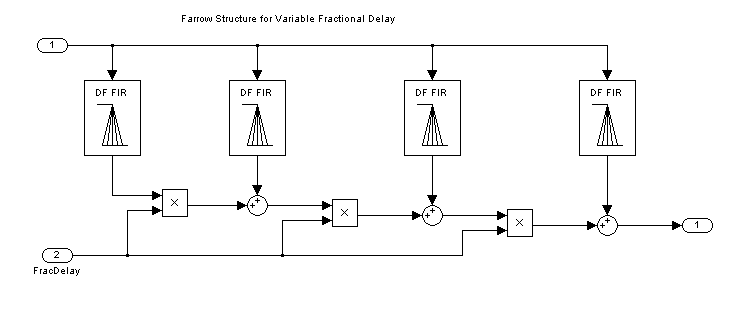
可能な限り平坦な FIR 近似 (ラグランジュ内挿)
ラグランジュ内挿は、多項式ベースのフィルターの特殊なケースとなる時間領域のアプローチで、出力信号を次数 M の多項式で近似します。最も単純なケース (M = 1) は線形内挿に相当します。さまざまな割合で単位遅延を分割する線形非整数遅延フィルターを設計して解析します。
Nx = 1024; Nf = 5; yw = zeros(Nx,Nf); transferFuncEstimator = dsp.TransferFunctionEstimator( ... SpectralAverages=25,FrequencyRange="onesided"); arrPlotPhaseDelay = dsp.ArrayPlot(PlotType="Line",YLimits=[0 1.5], ... YLabel="Phase delay",SampleIncrement=1/512); arrPlotMag = dsp.ArrayPlot(PlotType="Line",YLimits=[-10 1], ... YLabel="Magnitude (dB)",SampleIncrement=1/512); fracDelay = dsp.VariableFractionalDelay; xw = randn(Nx,Nf); transferFuncEstimator(xw,yw); w = getFrequencyVector(transferFuncEstimator,2*pi); w = repmat(w,1,Nf); tic, while toc < 2 yw = fracDelay(xw,[0 0.2 0.4 0.6 0.8]); H = transferFuncEstimator(xw,yw); arrPlotMag(20*log10(abs(H))) arrPlotPhaseDelay(-angle(H)./w) end release(fracDelay) release(transferFuncEstimator) release(arrPlotMag)
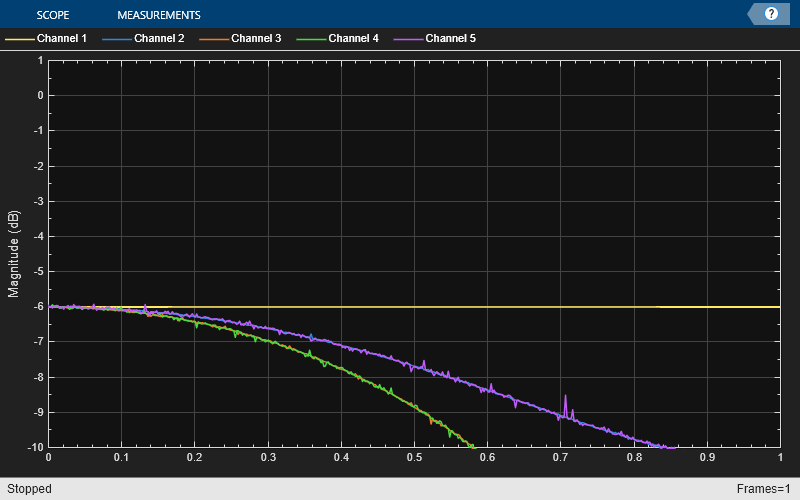
release(arrPlotPhaseDelay)
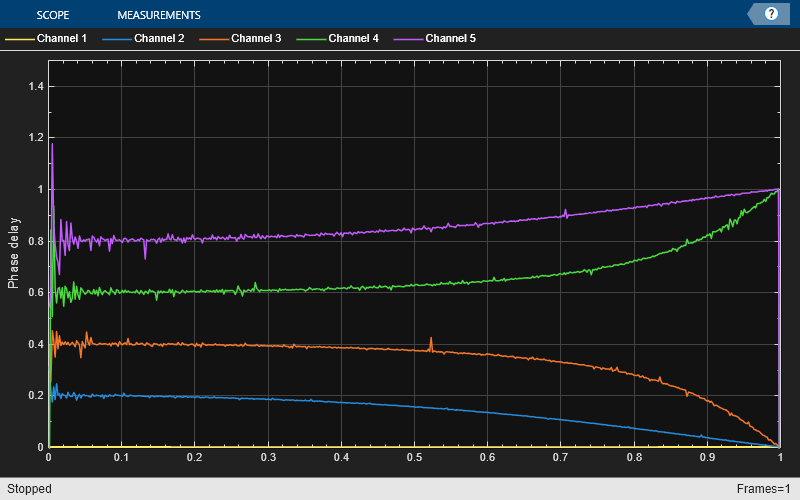
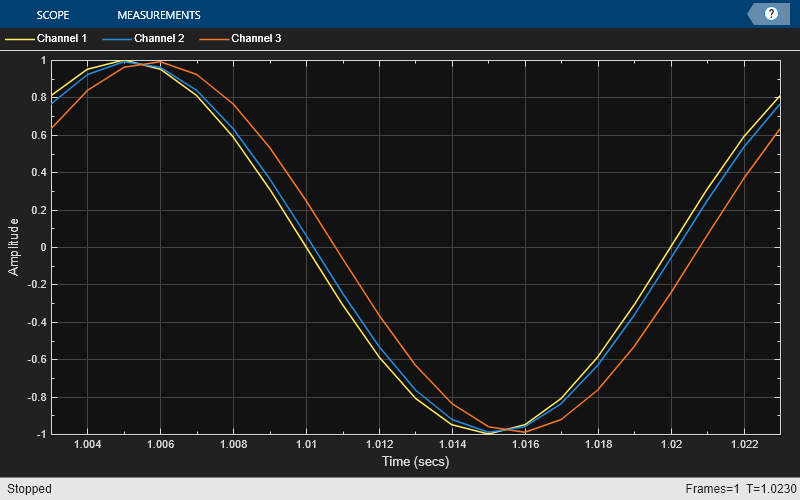
いかなる遅延値に対しても、理想的なフィルターは平坦な振幅応答と平坦な位相遅延応答の両方をもっていなければなりません。近似は最小周波数に対してのみ正しくなります。したがって、実際に線形非整数遅延が正しく機能するには、信号をオーバーサンプリングする必要があります。この手順では、2 つの異なる非整数遅延を正弦波に適用し、時間スコープを使用して元の正弦波と 2 つの遅延バージョンを重ねます。サンプル レート 1000 Hz における 0.2 サンプルの遅延は、0.2 ms の遅延に相当します。
scope = timescope(SampleRate=1000, ... YLimits=[-1 1], ... TimeSpan=.02, ... TimeSpanOverrunAction="scroll"); sine = dsp.SineWave(Frequency=50, SamplesPerFrame=Nx); tic, while toc < 2 x = sine(); y = fracDelay(x,[.2 .8]); % Delay by 0.2 and 0.8 samples (i.e. 0.2ms and 0.8ms respectively) scope([x,y(:,1),y(:,2)]) end release(fracDelay) release(scope);
より高次のラグランジュ内挿器を設計できます。3 次ラグランジュ内挿器と線形ラグランジュ内挿器を比較します。
farrowFracDelay = dsp.VariableFractionalDelay( ... InterpolationMethod="Farrow",MaximumDelay=1025); Nf = 2; yw = zeros(Nx,Nf); xw = randn(Nx,Nf); H = transferFuncEstimator(xw,yw); w = getFrequencyVector(transferFuncEstimator,2*pi); w = repmat(w,1,Nf); tic, while toc < 2 % Run for 2 seconds yw(:,1) = fracDelay(xw(:,1),0.4); % Delay by 0.4 samples (0.4ms) yw(:,2) = farrowFracDelay(xw(:,2),1.4); % Delay by 1.4 samples (1.4ms) H = transferFuncEstimator(xw,yw); arrPlotMag(20*log10(abs(H))) arrPlotPhaseDelay(-unwrap(angle(H))./w) end release(fracDelay) release(transferFuncEstimator) release(arrPlotMag)
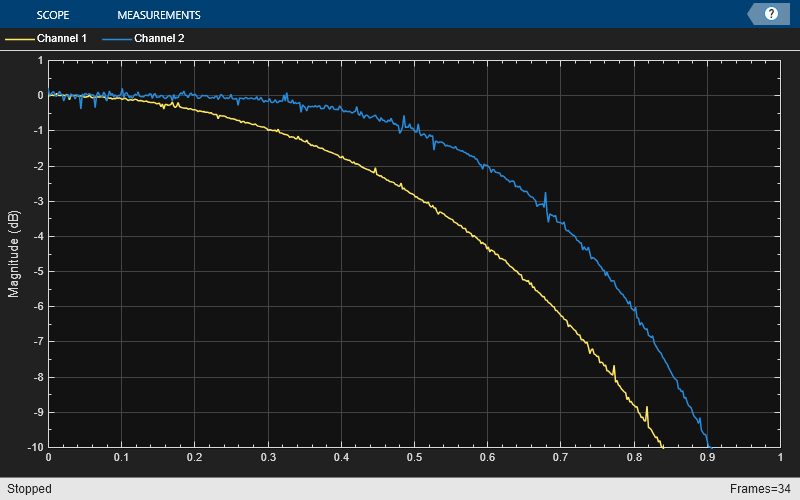
release(arrPlotPhaseDelay)
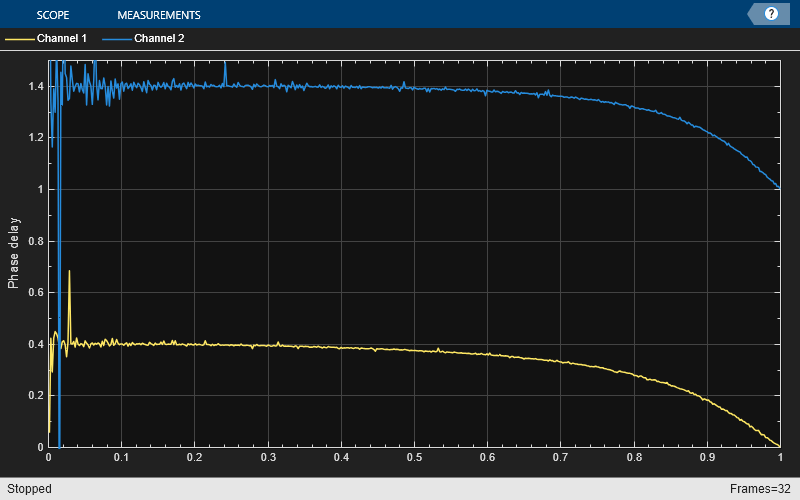
多項式の次数を増やすと、ラグランジュ近似を使用する場合に有用な帯域幅がわずかに増加します。微分フィルターの長さ、つまりインパルス応答の区分数 ('Coefficients' プロパティの行数) は、多項式の長さ ('Coefficients' プロパティの列数) と等しくなります。他の設計法を使用してこの制限を克服することもできます。3 次フィルターの位相遅延は、DC で 0.4 サンプルから 1.4 サンプルにシフトします。3 次ラグランジュ内挿器は 3 次フィルターであるため、達成可能な最小遅延は 1 になります。そのため、この場合の遅延は 0.4 ms ではなく 1.4 ms になります。
sine = dsp.SineWave(Frequency=50,SamplesPerFrame=Nx); tic, while toc < 2 x = sine(); y1 = fracDelay(x,0.4); y2 = farrowFracDelay(x,1.4); scope([x,y1,y2]) end release(fracDelay) release(scope);
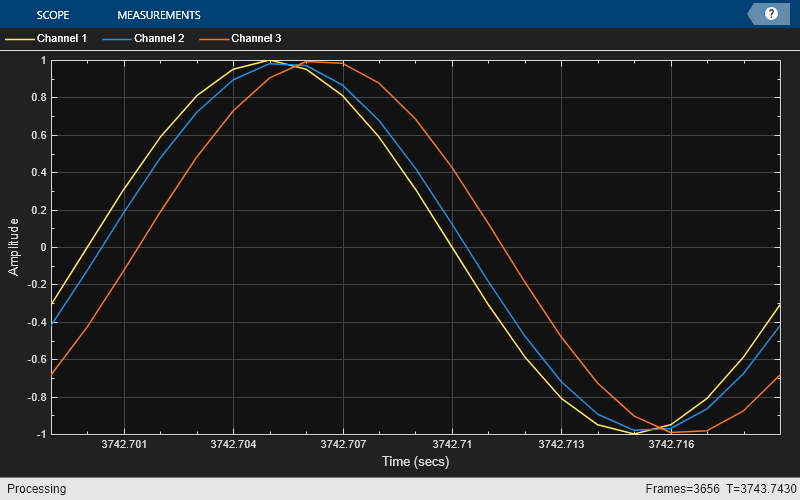
時変非整数遅延
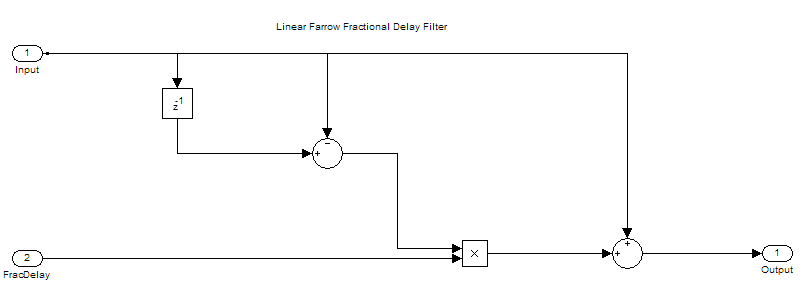
直接型 FIR と比較した Farrow 構造の利点は、その調整可能性にあります。数多くの実用アプリケーションにおいて、遅延は時間とともに変化します。新しい各遅延に対し、直接型実装では新しい係数セットが必要になりますが、Farrow の実装では、多項式の係数は一定のままです。
tic, while toc < 5 x = sine(); if toc < 1 delay = 1; elseif toc < 2 delay = 1.2; elseif toc < 3 delay = 1.4; elseif toc < 4 delay = 1.6; else delay = 1.8; end y = farrowFracDelay(x,delay); scope([x,y]) end release(fracDelay) release(scope);